
Los/las mejores profesores/as de Matemáticas que están disponibles

5 (349 opiniones)

¡1a clase gratis!

4,9 (74 opiniones)

¡1a clase gratis!

5 (66 opiniones)

¡1a clase gratis!

5 (38 opiniones)

¡1a clase gratis!

5 (136 opiniones)

¡1a clase gratis!

5 (35 opiniones)

¡1a clase gratis!

5 (31 opiniones)

¡1a clase gratis!

5 (301 opiniones)

¡1a clase gratis!

5 (349 opiniones)

¡1a clase gratis!

4,9 (74 opiniones)

¡1a clase gratis!

5 (66 opiniones)

¡1a clase gratis!

5 (38 opiniones)

¡1a clase gratis!

5 (136 opiniones)

¡1a clase gratis!

5 (35 opiniones)

¡1a clase gratis!

5 (31 opiniones)

¡1a clase gratis!

5 (301 opiniones)

¡1a clase gratis!
Vamos
Ejercicios
1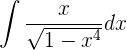
Solución:

2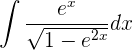
Solución:
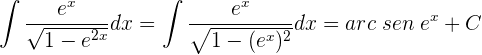
3
Solución:
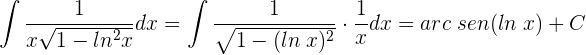
4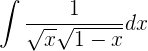
Solución:
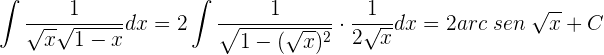
5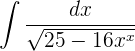
Solución:

6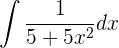
Solución:
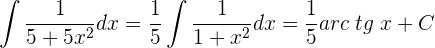
7
Solución:

8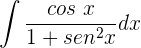
Solución:

9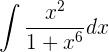
Solución:
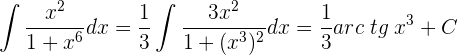
10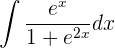
Solución:

11
Solución:
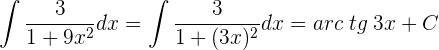
12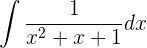
Vamos a transformar el denominador de modo que podamos aplicar la fórmula de la integral del arcotangente.
Transformamos el denominador en un binomio al cuadrado.

Multiplicamos numerador y denominador por  , para obtener uno en el denominador.
, para obtener uno en el denominador.
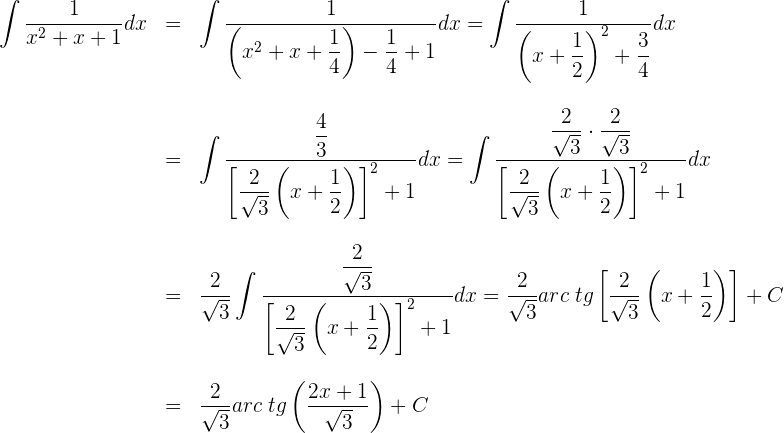

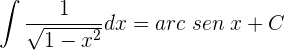


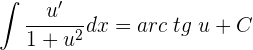

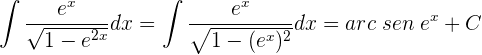

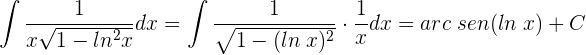
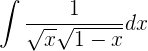
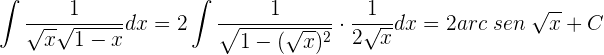
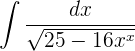

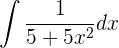
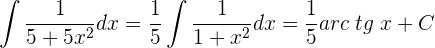


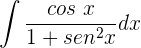

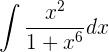
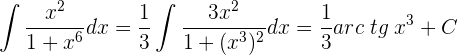
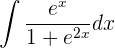


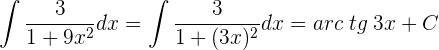
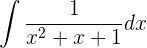

 , para obtener uno en el denominador.
, para obtener uno en el denominador.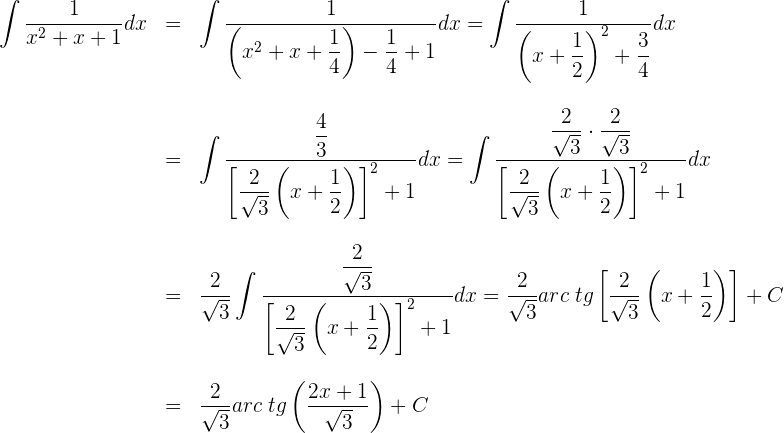













me puedes indicar por favor como desarrollar la integral e^x^2 sin (x) dx
Fe de erratas:
Ej. 3: sobra una raíz de x en el denominador antes del
Resultado final.
Ej.4: En el resultado final falta el signo menos.
Un saludo.
Hola revise los ejemplos de muchas ejercicios y no encontré los errores, podrías hacerme el favor de darme mas detalles para poder encontrarlos y quitar esos errores, seria de mucha ayuda.
Podrían brindarme información sobre el autor y la fecha de publicación del articulo? Estoy realizando una monografía en matemáticas y esta agina me ha servido mucho pero necesito esa información para referenciar correctamente la información.
¡Hola Yanela! 👋 Desde Superprof nos alegra que el artículo te haya sido útil. 😊 Para referenciarlo correctamente en tu monografía, puedes citarlo de la siguiente manera:
«Superprof. Ejercicios resueltos de integrales por sustitución. [En línea] Disponible en: [URL del artículo].»
Por motivos de privacidad, no podemos facilitar datos personales del autor ni fecha exacta de publicación. 📚✨
Veo un error en el ejercicio 9 a la hora de devolver la variable, recuerda que x^2+1 = u^2, no x^2+1 = u
Hola tienes razón, una disculpa y ya se corrigió.
Hola la manera en como presentas la fórmula esta bien, pero en la propiedad 4 que mencionas es lo mismo pero escrita de forma diferente, si multiplicas por el signo negativo queda igual a lo que tienes, si tienen alguna duda mencionalo.
holaa, en el caso 4, en la última identidad están mal los signos, sería sen(a)sen(b)=1/2(cos(a-b)-cos(a+b))