El estudio de los vectores es fundamental en matemáticas, física e ingeniería, ya que permiten describir magnitudes que poseen tanto dirección como sentido. Entre las operaciones más importantes con vectores se encuentran el producto escalar y el producto vectorial, herramientas que facilitan el análisis de problemas geométricos y físicos.
El producto escalar (o producto punto) permite relacionar dos vectores mediante un número real, lo cual resulta útil para calcular ángulos, proyecciones y verificar la perpendicularidad entre vectores. Por su parte, el producto vectorial genera un nuevo vector perpendicular a los vectores dados, siendo esencial para describir áreas, momentos y fenómenos tridimensionales.
Dados los vectores 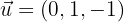 y
y 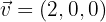 , hallar:
, hallar:
aLos módulos de  y
y 
bEl producto vectorial de  y
y 
cUn vector unitario ortogonal a  y
y 
dEl área del paralelogramo que tiene por lados los vectores y
y 
aLos módulos de  y
y 
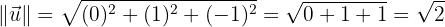
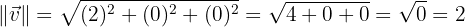
bEl producto vectorial de 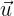 y
y 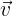
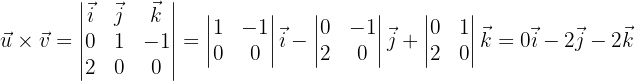
cUn vector unitario ortogonal a  y
y 
Cuando se calcula el producto vectorial entre dos vectores, se genera un vector ortogonal a ambos, por tal razón
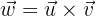
es el vector ortogonal que necesitamos, ahora sólo hace falta hacerlo unitario, primero calculemos su módulo
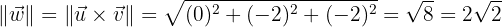
y entonces ya podemos hacerlo unitario
dEl área del paralelogramo que tiene por lados los vectores y
y 
El área del paralelogramo, se calcula con el módulo del producto vectorial de los vectores que lo conforman
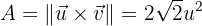
Dados los vectores 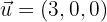 y
y 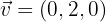 , hallar:
, hallar:
aLos módulos de  y
y 
bEl producto vectorial de  y
y 
cUn vector unitario ortogonal a  y
y 
dEl área del paralelogramo que tiene por lados los vectores y
y 
aLos módulos de  y
y 
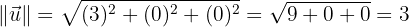
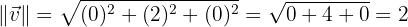
bEl producto vectorial de  y
y 
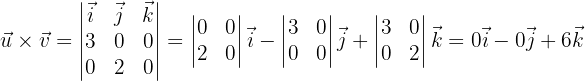
cUn vector unitario ortogonal a  y
y 
Cuando se calcula el producto vectorial entre dos vectores, se genera un vector ortogonal a ambos, por tal razón
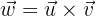
es el vector ortogonal que necesitamos, ahora sólo hace falta hacerlo unitario, primero calculemos su módulo
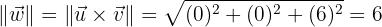
y entonces ya podemos hacerlo unitario
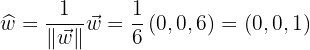
dEl área del paralelogramo que tiene por lados los vectores y
y 
El área del paralelogramo, se calcula con el módulo del producto vectorial de los vectores que lo conforman
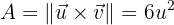
Dados los vectores 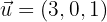 y
y 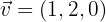 , hallar:
, hallar:
aLos módulos de  y
y 
bEl producto vectorial de  y
y 
cUn vector unitario ortogonal a  y
y 
dEl área del paralelogramo que tiene por lados los vectores y
y 
aLos módulos de  y
y 
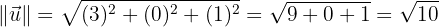
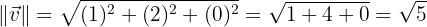
bEl producto vectorial de  y
y 
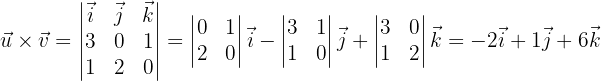
cUn vector unitario ortogonal a  y
y 
Cuando se calcula el producto vectorial entre dos vectores, se genera un vector ortogonal a ambos, por tal razón
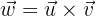
es el vector ortogonal que necesitamos, ahora sólo hace falta hacerlo unitario, primero calculemos su módulo
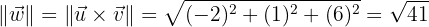
y entonces ya podemos hacerlo unitario
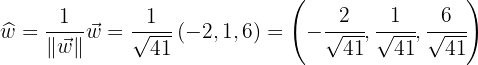
dEl área del paralelogramo que tiene por lados los vectores y
y 
El área del paralelogramo, se calcula con el módulo del producto vectorial de los vectores que lo conforman
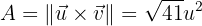
Dados los vectores  y
y 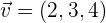 , hallar:
, hallar:
aLos módulos de  y
y 
bEl producto vectorial de  y
y 
cUn vector unitario ortogonal a  y
y 
dEl área del paralelogramo que tiene por lados los vectores y
y 
aLos módulos de  y
y 

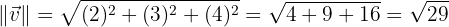
bEl producto vectorial de  y
y 
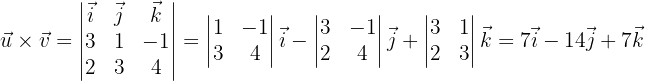
cUn vector unitario ortogonal a  y
y 
Cuando se calcula el producto vectorial entre dos vectores, se genera un vector ortogonal a ambos, por tal razón
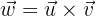
es el vector ortogonal que necesitamos, ahora sólo hace falta hacerlo unitario, primero calculemos su módulo

y entonces ya podemos hacerlo unitario
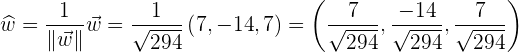
dEl área del paralelogramo que tiene por lados los vectores y
y 
El área del paralelogramo, se calcula con el módulo del producto vectorial de los vectores que lo conforman
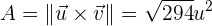
Hallar el ángulo que forman los vectores 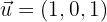 y
y 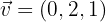
Sea
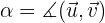
el ángulo formado entre los vectores.
Calculemos entonces el coseno de dicho ángulo
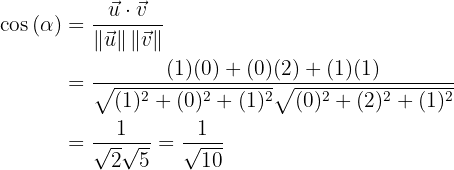
entonces ahora apliquemos la inversa del coseno sobre el valor calculado, para conocer el valor del ángulo formado entre los vectores
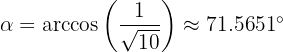
Hallar el ángulo que forman los vectores  y
y 
Sea
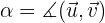
el ángulo formado entre los vectores.
Calculemos entonces el coseno de dicho ángulo
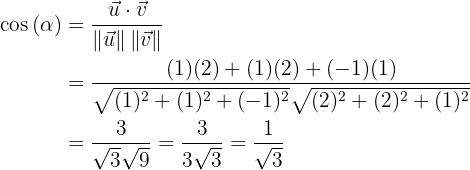
entonces ahora apliquemos la inversa del coseno sobre el valor calculado, para conocer el valor del ángulo formado entre los vectores

Hallar los cosenos directores del vector 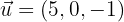
Los cosenos directores, sirven para saber el ángulo generado entre cada eje y el vector respectivamente, es decir, sirven como una herramienta de localización de un punto
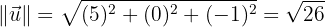
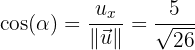
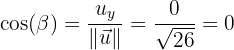
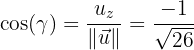
Hallar los cosenos directores del vector 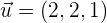
Los cosenos directores, sirven para saber el ángulo generado entre cada eje y el vector respectivamente, es decir, sirven como una herramienta de localización de un punto


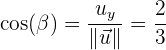

Dados los vectores 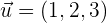 ,
, 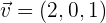 y
y 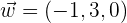 , hallar:
, hallar:
a
b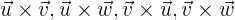
c y
y 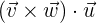
d
e y
y 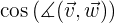
a
Antes de realizar el ejercicio, recordemos:
Si tenemos al vector 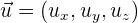 y al vector
y al vector  , definimos al producto escalar como:
, definimos al producto escalar como:
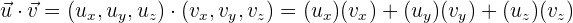
y de esta manera ya podemos desarrollar el ejercicio.

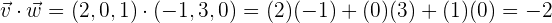
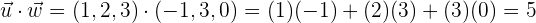
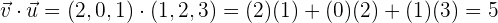
b
Usando la misma nomenclatura, definimos al producto vectorial como:
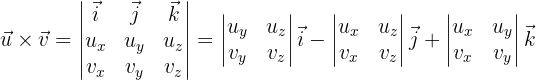
donde
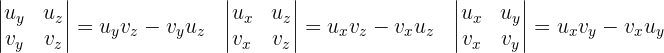
la cual nos permite desarrollar los ejercicios solicitados.
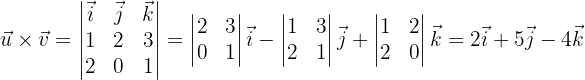
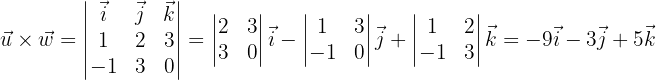
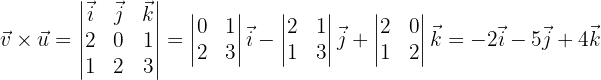
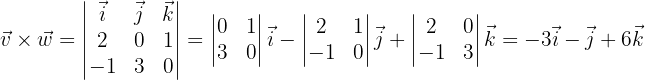
c y
y 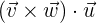
Una vez teniendo claras las definiciones de producto escalar y vectorial, podemos combinarlas entre ellas. No olvide que un producto escalar genera un número, y un producto vectorial un vector, debido a esta razón es importante el orden en que se realizan los productos, debido a eso los paréntesis. El producto final representa el volumen del paralelogramo generado por los vectores, y como son los mismo el volumen resulta igual en ambos casos.


4
Nuevamente, haciendo uso de la nomenclatura inicial, recordemos la definición del módulo de un vector
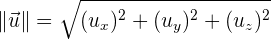
habiendo recordado la fórmula, ya podemos calcular
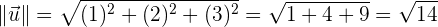

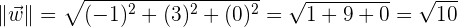
d y
y 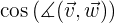
Con toda esta información, ya es posible calcular el coseno del ángulo formado entre los vectores.
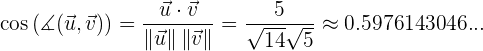

Dados los vectores  y
y 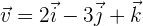 , hallar el producto
, hallar el producto  y comprobar que este vector es ortogonal a
y comprobar que este vector es ortogonal a  y a
y a  . Hallar el vector
. Hallar el vector 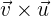 y compararlo con
y compararlo con 
Primero el producto vectorial
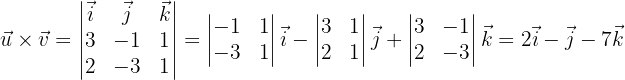
Ahora recordemos que para que dos vectores sean perpendiculares, su producto escalar debe ser cero

Verifiquemos:

ahora con el otro vector
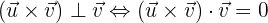
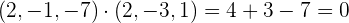
observando que efectivamente los vectores en cuestión son perpendiculares.
Ahora calculemos el siguiente producto vectorial, observe que los vectores ahora tienen distinto orden
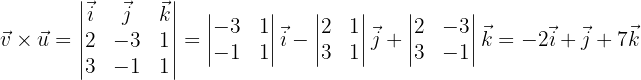
llegando así al ejemplo de una de las propiedades importantes del producto vectorial, la anticonmutatividad
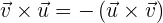



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Suma de vectores f1=450n,30. 1FR=f1+f6
como sacar el residuo de una multiplicación
Hallar las coordenadas de punto medio del segmento que une (4,7);(14,12)
Hola, podrias mencionar que tipo de multiplicación (normal, de vectores etc.).
si se aplica una traslación al punto E(0;2) se obtiene el punto E'(-1;-5),indicar el vector de translación
Traslaciones Juan es un diseñador gráfico y de acuerdo con las exigencias de uno de sus clientes debe reorganizar los elementos de uno de los avisos publicitarios observemos en la ilustración los cambios y desplazamientos que realizo.
En la ilustración el barco se trasladó dos unidades hacia arriba.
Una traslación es el desplazamiento de una figura sobre un plano sin girarla en ninguna dirección para indicar una traslación usamos una flecha que muestra el sentido hacia donde se hace el movimiento:
Derecha , izquierda, arriba, abajo, occidente, Oriente, Norte o sur) y la magnitud (número de unidades que se mueve la figura).
En el aviso publicitario,? Cuál de los siguientes desplazamientos se realizó con el logo del pez? Márcalo con x
Vectores 400n+horizontal y a la izquierda