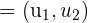 y
y  vectores, entonces tenemos las siguientes fórmulas del producto escalar de vectores, usualmente denotada con
vectores, entonces tenemos las siguientes fórmulas del producto escalar de vectores, usualmente denotada con 
1 Expresión analítica del producto escalar:
Tenemos que el producto escalar se define como
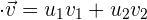
2Expresión analítica del módulo de un vector
Tenemos que el modulo de un vector se define de la siguiente manera
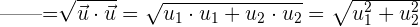
3 Producto escalar:
Podemos expresar el producto escalar utilizando módulos y el ángulo entre los vectores, obteniendo que
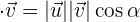
4 Expresión analítica del ángulo de dos vectores
Utilizando las fórmulas anteriores expresaremos el ángulo entre dos vectores
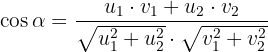
5 Expresión analítica de la ortogonalidad de dos vectores:
Dos vectores son ortogonales cuando forman un ángulo recto entre si. Si el producto escalar de dos vectores es cero, entonces son ortogonales, es decir, si
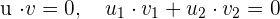
entonces ortogonales.
6 Proyección:
El producto escalar de dos vectores no nulos es igual al módulo de uno de ellos por la proyección del otro sobre él.
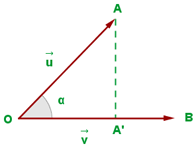
Esto se obtiene de:
Calcular el coseno del ángulo 
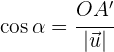
Despejamos 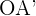 el cual es la proyección escalar de
el cual es la proyección escalar de  sobre el vector
sobre el vector 

Sabemos que 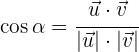 , luego
, luego

Simplificando se obtiene
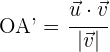
Despejando se obtiene
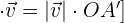
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Suma de vectores f1=450n,30. 1FR=f1+f6
como sacar el residuo de una multiplicación
Hallar las coordenadas de punto medio del segmento que une (4,7);(14,12)
Hola, podrias mencionar que tipo de multiplicación (normal, de vectores etc.).
si se aplica una traslación al punto E(0;2) se obtiene el punto E'(-1;-5),indicar el vector de translación
Traslaciones Juan es un diseñador gráfico y de acuerdo con las exigencias de uno de sus clientes debe reorganizar los elementos de uno de los avisos publicitarios observemos en la ilustración los cambios y desplazamientos que realizo.
En la ilustración el barco se trasladó dos unidades hacia arriba.
Una traslación es el desplazamiento de una figura sobre un plano sin girarla en ninguna dirección para indicar una traslación usamos una flecha que muestra el sentido hacia donde se hace el movimiento:
Derecha , izquierda, arriba, abajo, occidente, Oriente, Norte o sur) y la magnitud (número de unidades que se mueve la figura).
En el aviso publicitario,? Cuál de los siguientes desplazamientos se realizó con el logo del pez? Márcalo con x
Vectores 400n+horizontal y a la izquierda