Dados los vectores:
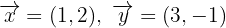
hallar la combinación lineal:
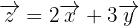
Lo primero que haremos es sustituir los valores de 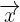 ,
, 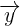 en la combinación lineal, por lo que tenemos:
en la combinación lineal, por lo que tenemos:
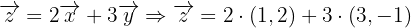
Ahora haremos la multiplicación por el escalar:
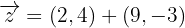
Por lo que finalmente necesitamos hacer la suma de los vectores para resolver el problema:
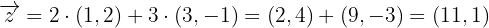
¿Se puede expresar el vector 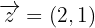 como combinación lineal de los vectores
como combinación lineal de los vectores 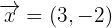 ,
, 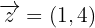 ?
?
Para averiguar si es posible expresar el vector 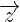 como combinación lineal de los vectores
como combinación lineal de los vectores 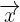 ,
, 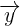 debemos encontrar escalares
debemos encontrar escalares  ,
,  tales que:
tales que:
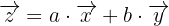
Si sustituimos los valores de 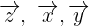 tenemos:
tenemos:
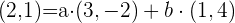
Podemos notar que esto es equivalente a resolver el sistema de ecuaciones;
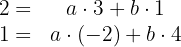
Para resolver esto tomamos la primera ecuación y despejamos para  , por lo que obtenemos:
, por lo que obtenemos:
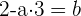
Ahora sustituimos el valor de  en la segunda ecuación para obtener:
en la segunda ecuación para obtener:
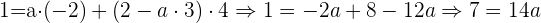
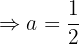
Por lo que se sigue que: 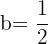 .
.
ya que encontramos pudimos encontrar escalares  ,
,  tales que:
tales que:
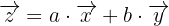
Entonces concluimos que el vector 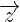 se puede expresar como combinación lineal de los vectores
se puede expresar como combinación lineal de los vectores 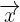 ,
, 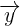 .
.
¿Qué pares de los siguientes vectores forman una base para el plano  ?
?
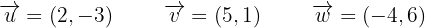
Dado que estamos buscando una base para el plano  , sabemos que dos vectores forman una base si no son linealmente dependientes, y a su vez tenemos que dos vectores son linealmente dependientes si uno es un múltiplo escalar del otro.Es decir basta con ver si en un par de vectores ninguno de ellos es múltiplo de otro para que sean una base.Ahora dados dos vectores
, sabemos que dos vectores forman una base si no son linealmente dependientes, y a su vez tenemos que dos vectores son linealmente dependientes si uno es un múltiplo escalar del otro.Es decir basta con ver si en un par de vectores ninguno de ellos es múltiplo de otro para que sean una base.Ahora dados dos vectores 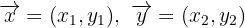 decimos que uno es múltiplo del otro si
decimos que uno es múltiplo del otro si 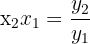 Empezamos por tomar los vectores
Empezamos por tomar los vectores 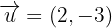 y
y 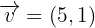 , notamos que:
, notamos que:
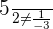
Por lo que 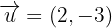 y
y 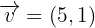 forman una base para el plano.Tomamos ahora los vectores
forman una base para el plano.Tomamos ahora los vectores 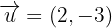 y
y 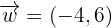 y notamos que:
y notamos que:
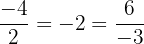
Por lo que 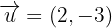 y
y 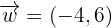 no forman una base para el plano.
no forman una base para el plano.
Por ultimo tomamos los vectores 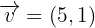 y
y 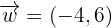 , y notamos que:
, y notamos que:
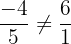
Por lo que 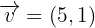 y
y 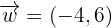 forman una base para el plano.
forman una base para el plano.
Hallar un vector unitario  de la misma dirección del vector
de la misma dirección del vector 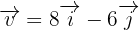
La formula para encontrar un vector unitario  de la misma dirección de un vector
de la misma dirección de un vector  está dada por:
está dada por:
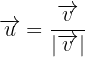
Donde 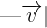 representa la norma del vector
representa la norma del vector  .Por lo que sustituyendo los valores que nos han dado tenemos que:
.Por lo que sustituyendo los valores que nos han dado tenemos que:
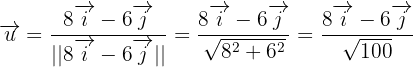
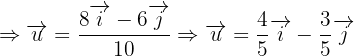
Suponiendo que respecto de la base ortonormal 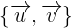 del plano los vectores
del plano los vectores 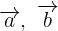 tienen como expresiones:
tienen como expresiones:

calcular el valor de  sabiendo que
sabiendo que 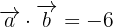
Sustituyendo los respectivos valores de 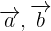 en la expresión
en la expresión 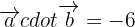 y desarrollando obtenemos lo siguiente:
y desarrollando obtenemos lo siguiente:
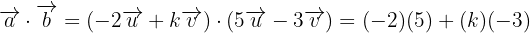
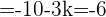
Por lo que despejando  de esta última expresión tenemos que:
de esta última expresión tenemos que:
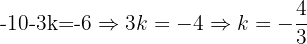
Dados los vectores 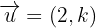 y
y 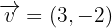 , calcula
, calcula  para que los vectores
para que los vectores  y
y  sean:
sean:
aPerpendiculares.
bParalelos.
cFormen un ángulo de  .
.
aSi queremos que los vectores sean perpendiculares entonces debemos elegir un valor de  tal que:
tal que:
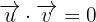
Si sustituimos los valores de ambos vectores en esta última ecuación y luego la desarrollamos, obtenemos:
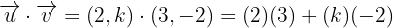
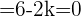
Por lo que despejando  en esta última expresión tenemos:
en esta última expresión tenemos:
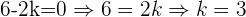
bPedir que dos vectores sean paralelos es equivalente a pedir que uno de los vectores sea un múltiplo escalar del otro, por lo que debemos elegir un valor de  tal que:
tal que:
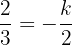
El cual podemos obtener fácilmente despejando  de esta última expresión, si lo hacemos obtenemos:
de esta última expresión, si lo hacemos obtenemos:
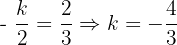
cEl ángulo que forman dos vectores 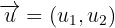 y
y 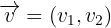 viene dado por la expresión:
viene dado por la expresión:
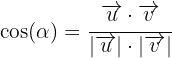
Donde 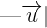 representa la norma del vector
representa la norma del vector  (similar para
(similar para  ), y
), y  es el ángulo entre los vectores.Entonces si buscamos que el ángulo entre los vectores sea
es el ángulo entre los vectores.Entonces si buscamos que el ángulo entre los vectores sea  significa que:
significa que:
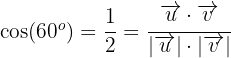
Por ende sustituyendo el valor de  y
y  en esta última expresión tenemos:
en esta última expresión tenemos:
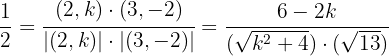
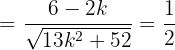
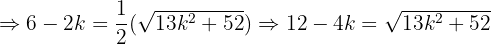
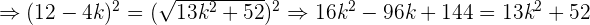

Ahora solo nos falta usar la formula general de segundo grado para encontrar las soluciones de la última expresión, las cuales son:

Hallar  si el ángulo que forma
si el ángulo que forma 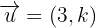 con
con 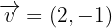 es:
es:
a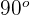
b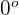
cFormen un ángulo de 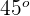
a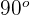
Si el ángulo entre los vectores es de 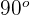 entonces los vectores son perpendiculares por lo que el valor de
entonces los vectores son perpendiculares por lo que el valor de  de ser tal que:
de ser tal que:
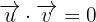
Si sustituimos los valores de ambos vectores en esta última ecuación y luego la desarrollamos, obtenemos:
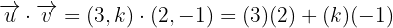

Por lo que despejando  en esta última expresión tenemos:
en esta última expresión tenemos:
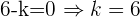
b
Si el ángulo entre dos vectores es 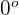 significa que los vectores son paralelos, lo cual es equivalente a pedir que uno de los vectores sea un múltiplo escalar del otro, por lo que debemos encontrar un valor de
significa que los vectores son paralelos, lo cual es equivalente a pedir que uno de los vectores sea un múltiplo escalar del otro, por lo que debemos encontrar un valor de  tal que:
tal que:
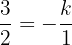
El cual podemos obtener fácilmente despejando  de esta última expresión, si lo hacemos obtenemos:
de esta última expresión, si lo hacemos obtenemos:
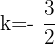
cFormen un ángulo de 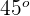
El ángulo que forman dos vectores 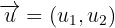 y
y 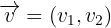 viene dado por la expresión:
viene dado por la expresión:
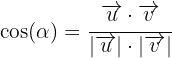
Donde 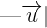 representa la norma del vector
representa la norma del vector  (similar para
(similar para  ), y
), y  es el ángulo entre los vectores.Entonces si buscamos que el ángulo entre los vectores sea
es el ángulo entre los vectores.Entonces si buscamos que el ángulo entre los vectores sea 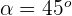 significa que:
significa que:
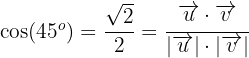
Por ende sustituyendo el valor de  y
y  en esta última expresión tenemos:
en esta última expresión tenemos:
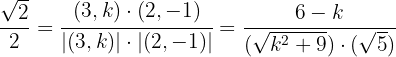
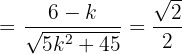
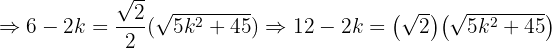


Ahora solo nos falta usar la formula general de segundo grado para encontrar las soluciones de la última expresión, las cuales son:

Suponiendo que respecto a la base ortonormal 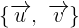 del plano los vectores
del plano los vectores 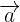 y
y  tienen como expresiones:
tienen como expresiones:
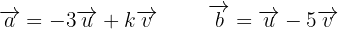
Calcular el valor de  para que los dos vectores sean ortogonales.
para que los dos vectores sean ortogonales.
Si dos vectores 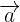 y
y  son ortogonales entonces se cumple:
son ortogonales entonces se cumple: 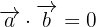 . Entonces debemos buscar un valor de
. Entonces debemos buscar un valor de  tal que esto ocurra, para encontrarlo sustituimos los valores de los vectores desarrollamos esa expresión.
tal que esto ocurra, para encontrarlo sustituimos los valores de los vectores desarrollamos esa expresión.
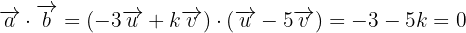
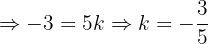
Calcular los ángulos del triángulo de vértices: 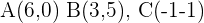
El ángulo que forman dos vectores 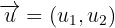 y
y 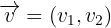 viene dado por la expresión:
viene dado por la expresión:
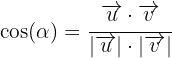
Donde 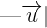 representa la norma del vector
representa la norma del vector  (similar para
(similar para  ), y
), y  es el ángulo entre los vectores.En este caso podemos tomar como vectores los segmentos que conectan los puntos del triángulo de la siguiente manera:
es el ángulo entre los vectores.En este caso podemos tomar como vectores los segmentos que conectan los puntos del triángulo de la siguiente manera:
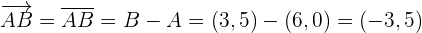

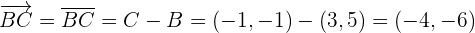
Primero vamos a encontrar el ángulo  que se encuentra entre los vectores
que se encuentra entre los vectores  y
y  con la fórmula mencionada al inicio, por lo que hacemos:
con la fórmula mencionada al inicio, por lo que hacemos:
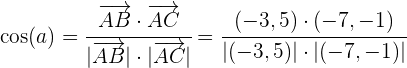
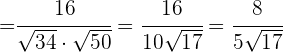
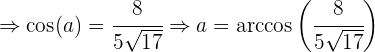
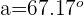
Ahora vamos a encontrar el ángulo  que se encuentra entre los vectores
que se encuentra entre los vectores  y
y 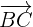 con la fórmula mencionada al inicio, por lo que hacemos:
con la fórmula mencionada al inicio, por lo que hacemos:
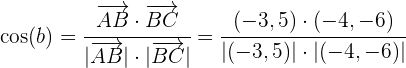

Dado que 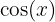 es una función par entonces
es una función par entonces  , por lo que usando esto tenemos que:
, por lo que usando esto tenemos que:
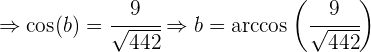
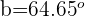
Para encontrar el valor del último ángulo  podemos usar el mismo proceso que usamos para los anteriores, pero usaremos el hecho de que la suma de los ángulos internos de un triángulo es igual a
podemos usar el mismo proceso que usamos para los anteriores, pero usaremos el hecho de que la suma de los ángulos internos de un triángulo es igual a 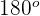 , por lo que tenemos que:
, por lo que tenemos que:


Calcula la proyección del vector  sobre él vector
sobre él vector  , siendo
, siendo  .
.
La proyección del vector  sobre el vector
sobre el vector  está dada por la fórmula:
está dada por la fórmula:
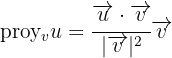
donde 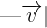 es la norma del vector
es la norma del vector  .Entonces sustituyendo los valores de los vectores
.Entonces sustituyendo los valores de los vectores  y
y  en esta fomula tenemos:
en esta fomula tenemos:
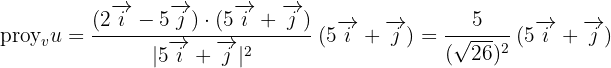
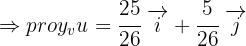
Calcula la proyección del vector  sobre él vector
sobre él vector  , siendo
, siendo  .
.
Primero vamos a calcular los componentes de los vectores  y
y 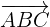 los cuales son:
los cuales son:

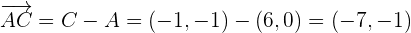
Ahora la proyección de un vector  sobre el vector
sobre el vector  está dada por la fórmula:
está dada por la fórmula:
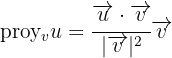
Por lo que si sustituimos los valores de los vectores del problema tenemos:
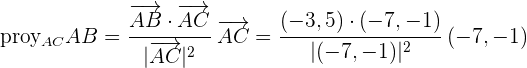
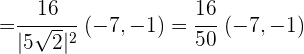

Comprobar que el segmento de une los puntos medios de los lados  y
y  del triángulo:
del triángulo: 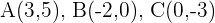 , es paralelo al lado
, es paralelo al lado  e igual a su mitad.
e igual a su mitad.

Lo primero que tenemos que hacer es encontrar el punto medio de los lados  y
y  , el cual lo podemos calcular con la siguiente fórmula:
, el cual lo podemos calcular con la siguiente fórmula:
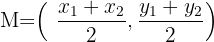
Por lo que el punto medio del lado  es:
es:
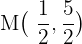
y en cuanto al punto medio del lado  es:
es:
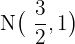
Por lo que el segmento que une los puntos medios de estos lados es 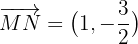 Ahora el segmento
Ahora el segmento 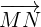 es paralelo al lado
es paralelo al lado 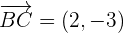 si sus componentes son proporcionales (uno de ellos es múltiplo del otro).Dados dos vectores
si sus componentes son proporcionales (uno de ellos es múltiplo del otro).Dados dos vectores 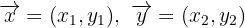 decimos que uno es múltiplo del otro si
decimos que uno es múltiplo del otro si 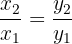 Entonces si usamos esto último podemos averiguar si los vectores
Entonces si usamos esto último podemos averiguar si los vectores 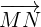 ,
, 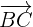 son paralelos, por lo que sustituimos sus componetes en esta expresión y tenemos:
son paralelos, por lo que sustituimos sus componetes en esta expresión y tenemos:
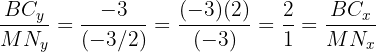
Por lo que efectivamente el segmento 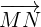 es paralelo al lado
es paralelo al lado 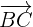 .
.
Si 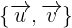 forma una base ortonormal, calcular:
forma una base ortonormal, calcular:
1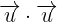 .
.
2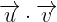 .
.
3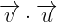 .
.
4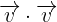 .
.
Debido a que los vectores 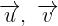 forman una base ortonormal significa que la norma de cada uno de ellos es igual a
forman una base ortonormal significa que la norma de cada uno de ellos es igual a  .
.
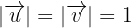
Ahora sabemos que el ángulo  entre dos vectores
entre dos vectores 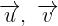 esta dado por:
esta dado por:
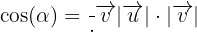
Por lo que podemos reescribir esta expresión de la siguiente forma:
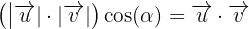
Entonces usando esta última expresión tenemos:1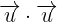 Dado que estamos calculando el producto punto entre dos vectores iguales, entonces el ángulo entre ellos es
Dado que estamos calculando el producto punto entre dos vectores iguales, entonces el ángulo entre ellos es  y su norma es
y su norma es  por ser vectores pertenecientes a la base ortonormal, por lo que tenemos que:
por ser vectores pertenecientes a la base ortonormal, por lo que tenemos que:
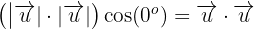
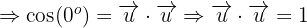
2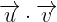 Dado que estamos calculando el producto punto entre dos vectores pertenecientes a la base ortonormal, esto indica que el ángulo entre los dos es
Dado que estamos calculando el producto punto entre dos vectores pertenecientes a la base ortonormal, esto indica que el ángulo entre los dos es 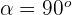 y su norma es
y su norma es  , por lo que tenemos que:
, por lo que tenemos que:
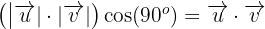
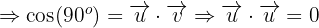
3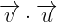 Dado que estamos calculando el producto punto entre dos vectores pertenecientes a la base ortonormal, esto indica que el ángulo entre los dos es
Dado que estamos calculando el producto punto entre dos vectores pertenecientes a la base ortonormal, esto indica que el ángulo entre los dos es 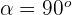 y su norma es
y su norma es  , por lo que tenemos que:
, por lo que tenemos que:
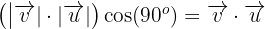
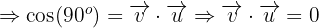
4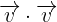 Dado que estamos calculando el producto punto entre dos vectores iguales, entonces el ángulo entre ellos es
Dado que estamos calculando el producto punto entre dos vectores iguales, entonces el ángulo entre ellos es  y su norma es
y su norma es  por ser vectores pertenecientes a la base ortonormal, por lo que tenemos que:
por ser vectores pertenecientes a la base ortonormal, por lo que tenemos que:
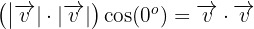
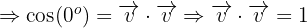
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Suma de vectores f1=450n,30. 1FR=f1+f6
como sacar el residuo de una multiplicación
Hallar las coordenadas de punto medio del segmento que une (4,7);(14,12)
Hola, podrias mencionar que tipo de multiplicación (normal, de vectores etc.).
si se aplica una traslación al punto E(0;2) se obtiene el punto E'(-1;-5),indicar el vector de translación
Traslaciones Juan es un diseñador gráfico y de acuerdo con las exigencias de uno de sus clientes debe reorganizar los elementos de uno de los avisos publicitarios observemos en la ilustración los cambios y desplazamientos que realizo.
En la ilustración el barco se trasladó dos unidades hacia arriba.
Una traslación es el desplazamiento de una figura sobre un plano sin girarla en ninguna dirección para indicar una traslación usamos una flecha que muestra el sentido hacia donde se hace el movimiento:
Derecha , izquierda, arriba, abajo, occidente, Oriente, Norte o sur) y la magnitud (número de unidades que se mueve la figura).
En el aviso publicitario,? Cuál de los siguientes desplazamientos se realizó con el logo del pez? Márcalo con x
Vectores 400n+horizontal y a la izquierda