Completa el punto simétrico que se piden en cada caso: (Simétrico de un punto respecto de otro):
Halla el punto simétrico de  respecto de
respecto de 
A' = ,
Este campo es obligatorio.
Recordemos que si  es el simétrico de
es el simétrico de  respecto de
respecto de  , entonces
, entonces  es el punto medio del segmento
es el punto medio del segmento  . Por lo que se verificará la igualdad:
. Por lo que se verificará la igualdad:

Ahora bien, supongamos que  , entonces
, entonces

por tanto
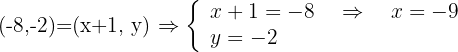
Halla el punto simétrico de  respecto de
respecto de  .
.
A' = ,
Este campo es obligatorio.
Supongamos que  , entonces
, entonces

por tanto
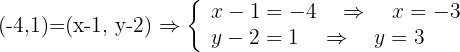
Halla el punto simétrico de  respecto de
respecto de 
A' = ,
Este campo es obligatorio.
Similar a los ejercicios anteriores, supongamos que  , entonces
, entonces

por tanto
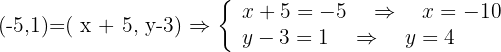
Halla el punto simétrico de  respecto de
respecto de 
A' = ,
Este campo es obligatorio.
Considerando que  , entonces
, entonces

por tanto
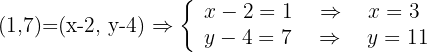
Completa el punto pedido en cada caso: (Simétrico de un punto respecto de otro):
Si  es el punto medio de
es el punto medio de  , siendo
, siendo  , halla el punto
, halla el punto  .
.
B = ,
Este campo es obligatorio.
Supongamos que  tiene coordenadas
tiene coordenadas  , al ser
, al ser  punto medio, se debe cumplir que
punto medio, se debe cumplir que
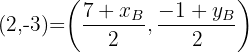
entonces
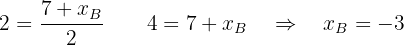
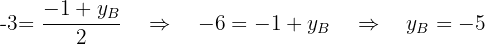
Si  es el punto medio de
es el punto medio de  , siendo
, siendo  halla el punto
halla el punto  .
.
B = ,
Este campo es obligatorio.
Nuevamente tenemos que  es el punto medio entre
es el punto medio entre  y
y  , considerando que
, considerando que  entonces
entonces
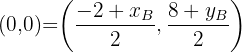
entonces
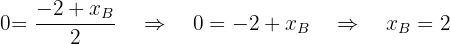

Resumir con IA:



Suma de vectores f1=450n,30. 1FR=f1+f6
como sacar el residuo de una multiplicación
Hallar las coordenadas de punto medio del segmento que une (4,7);(14,12)
Hola, podrias mencionar que tipo de multiplicación (normal, de vectores etc.).
si se aplica una traslación al punto E(0;2) se obtiene el punto E'(-1;-5),indicar el vector de translación
Traslaciones Juan es un diseñador gráfico y de acuerdo con las exigencias de uno de sus clientes debe reorganizar los elementos de uno de los avisos publicitarios observemos en la ilustración los cambios y desplazamientos que realizo.
En la ilustración el barco se trasladó dos unidades hacia arriba.
Una traslación es el desplazamiento de una figura sobre un plano sin girarla en ninguna dirección para indicar una traslación usamos una flecha que muestra el sentido hacia donde se hace el movimiento:
Derecha , izquierda, arriba, abajo, occidente, Oriente, Norte o sur) y la magnitud (número de unidades que se mueve la figura).
En el aviso publicitario,? Cuál de los siguientes desplazamientos se realizó con el logo del pez? Márcalo con x
Vectores 400n+horizontal y a la izquierda