Capítulos
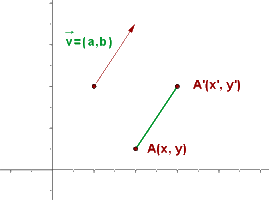
La traslación es una transformación puntual por la cual a todo punto 
del plano le corresponde otro punto 
también del plano de forma que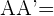 
, siendo 
el vector que define la traslación.
La traslación se designa por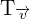 
, luego 
.
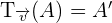El punto es el punto trasladado de .
Un punto y su trasladado se dice que son homólogos.
Coordenadas de un punto mediante una traslación
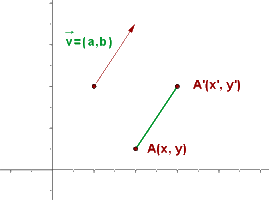
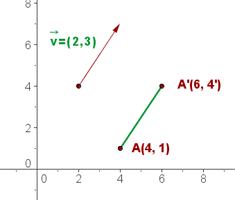
La traslación 
, definida por el vector del punto hacia el punto se puede entender mediante la siguiente fórmula.
Primero, detallamos cómo se escriben los dátos:
.
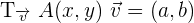El punto es igual al punto , más el vector :
.
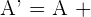Entonces,
.
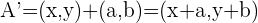donde,
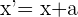
Ejemplo de traslación de un punto
En la representación gráfica, podemos observar el punto A que se traslada al punto A' mediante el vector .
Los datos de la traslación son los siguientes:
.
Sabemos que la coordenada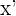 
se calcula mediante la fórmula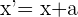
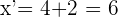
Calculamos ahora 
con la fórmula
Las coordenadas del punto son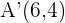 
Traslación de una recta
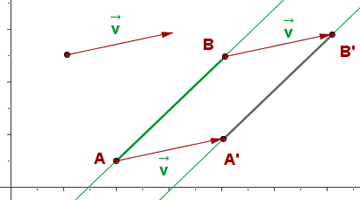
Una recta que se transforma, mediante una traslación, en una recta paralela.
Traslación de una circunferencia
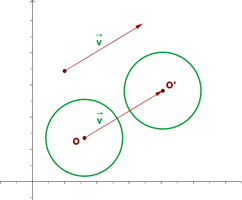
La homóloga de una circunferencia mediante una traslación es otra circunferencia de igual radio que tiene como centro el punto homólogo del centro de la circunferencia original.
Composición de traslaciones
Al aplicar sucesivamente dos traslaciones de vectores y 
, se obtiene otra traslación cuyo vector es la suma de los vectores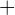 
, donde:
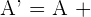
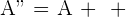
Ejercicios de traslaciones
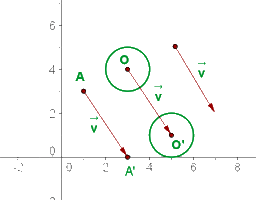
1Una traslación en el plano está definida por un vector 
a Hallar la imagen por dicha traslación de un punto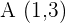 
.
b Hallar la transformada de una circunferencia que tiene de centro 
y de radio 
.
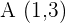. Primero, escribimos los datos del problema:
.
Usando la fórmula 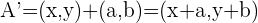para calcular la imágen, obtenemos:
.
.
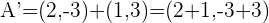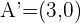b Hallar la transformada de una circunferencia que tiene de centro y de radio .
Primero, escribimos los datos del problema:
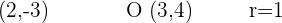
corresponde a las coordenadas del centro de la circunferencia y r su radio.
Usando, la misma fórmula que en el punto A, calculamos la imagen de O,
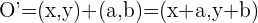y obtenemos:
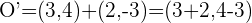
y la imagen del radio, 
sigue siendo igual que 
2 En una traslación mediante el vector , un punto 
se transforma en un punto 
.
Calcular:
a El transformado del punto 
.
b La transformada de una circunferencia de centro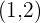 
y radio 
.
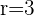, un punto se transforma en un punto .Calcular:
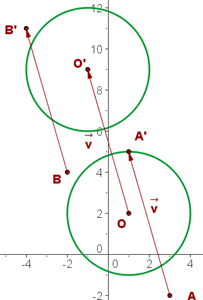
a El transformado del punto
. Primero, escribimos los datos del problema:
Para poder escribir el transformado del punto 
, que vamos a notar 
, necesitamos averiguar cual es el vector .
Sabemos que el vector se nota con las cooredenadas 
.
Usando la fórmula de la traslacion, competamos los datos conocidos (las coordenadas de los puntos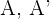 
:
.
.
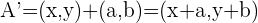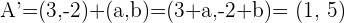Sabemos entoces que:
.
.
.
.
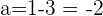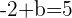Teniendo las coordenadas del vector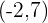 
, podemos calcular el transformado del punto 
.
Usando la misma fórmula,
.
Colocamos los datos conocidos:
,
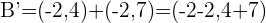y obtenemos:
.
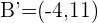b La transformada de una circunferencia de centro 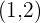y radio .
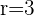Primero escribimos los datos del problema:
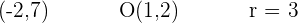
Y calculamos la transformada de la circunfencia, que notamos con 
, usando la misma fórmula:
.
.
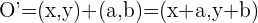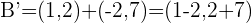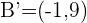y 
igual que .
3Una traslación tiene de vector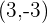 
. Hallar la figura transformada de un triángulo cuyos vértices son:
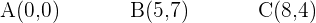
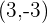. Hallar la figura transformada de un triángulo cuyos vértices son:Para poder dibujar la figura transformada, tenemos que averiguar las coordenadas de los puntos Una traslación tiene de vector 
y 
. Primero, escribimos los datos del problema:
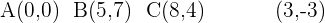
Usando la fórmula, calculamos cada una de las coordenadas:
.
.
.
.
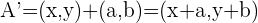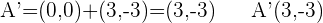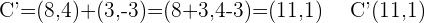Teniendo las coordenadas, podemos dibujar la figura:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Suma de vectores f1=450n,30. 1FR=f1+f6
como sacar el residuo de una multiplicación
Hallar las coordenadas de punto medio del segmento que une (4,7);(14,12)
Hola, podrias mencionar que tipo de multiplicación (normal, de vectores etc.).
si se aplica una traslación al punto E(0;2) se obtiene el punto E'(-1;-5),indicar el vector de translación
Traslaciones Juan es un diseñador gráfico y de acuerdo con las exigencias de uno de sus clientes debe reorganizar los elementos de uno de los avisos publicitarios observemos en la ilustración los cambios y desplazamientos que realizo.
En la ilustración el barco se trasladó dos unidades hacia arriba.
Una traslación es el desplazamiento de una figura sobre un plano sin girarla en ninguna dirección para indicar una traslación usamos una flecha que muestra el sentido hacia donde se hace el movimiento:
Derecha , izquierda, arriba, abajo, occidente, Oriente, Norte o sur) y la magnitud (número de unidades que se mueve la figura).
En el aviso publicitario,? Cuál de los siguientes desplazamientos se realizó con el logo del pez? Márcalo con x
Vectores 400n+horizontal y a la izquierda