Capítulos

¿Que es la regla de la cadena?
Muy seguido, aparecen funciones que presentan una estructura más elaborada y que se deben derivar, donde una derivación directa no es posible con las fórmulas habituales.
Por esta razón resulta útil conocer más herramientas y darnos cuenta de la forma en que ya es posible ir derivando a las funciones mencionadas.
Cuando nos referimos a funciones más elaboradas, hablamos de funciones que se construyen de la composición de otras dos.
Veamos, si tenemos a estas dos funciones
entonces podemos crear a una nueva función usando composición
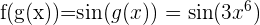
y con esto preguntarnos ¿cuál es la derivada de la nueva función  ?
?
Para responder esta pregunta, necesitamos utilizar la siguiente fórmula
Fórmula de la regla de la cadena

¿Cómo derivamos con la regla de la cadena?
La regla de la cadena, nos permite conocer la derivada de una función compuesta, utilizando las derivadas de las funciones que la componen, el proceso de derivación es muy simple y lo podemos efectuar siguiendo los siguientes pasos (utilicemos como referencia a la función mencionada):
- Si debemos derivar a la función
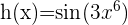 , que se construye de la composición de otras dos funciones
, que se construye de la composición de otras dos funciones 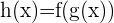 , lo primero que debemos hacer es identificar tanto a
, lo primero que debemos hacer es identificar tanto a 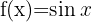 como a
como a 
- Una vez identificadas a las funciones, debemos derivar a
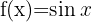

- Al resultado de la derivada de
 , lo debemos evaluar con
, lo debemos evaluar con 
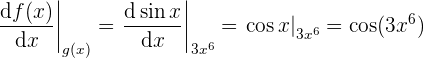
- Ahora derivemos a


- Finalmente multipliquemos a los dos resultados para tener a la derivada de

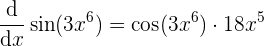
Con este proceso ya podemos tener a la derivada deseada. Es importante mencionar que con más práctica es posible efectuar el procedimiento de manera más rápida, una vez identificados los pasos a seguir claro.
Ejemplos de ejercicios usando la regla de la cadena
1 Derivar a la función 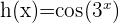
Sigamos el proceso:
- Identifiquemos a las funciones
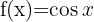 ,
, 
- Derivemos a


- Evaluemos el resultado con

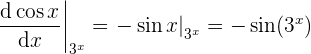
- Derivemos a

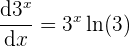
- Multipliquemos ambos resultados
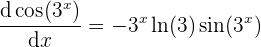
y con este proceso ya tenemos a la derivada de la función  .
.
Es importante mencionar, que existen ocasiones donde no solamente hay una composición, sino que puede haber varias, en ese caso la regla de la cadena sigue siendo válida, solamente que ahora la aplicamos varias veces hasta que terminemos de derivar.
El proceso también, lo desarrollaremos de manera directa sin mencionar los pasos en específico, el propósito es adquirir mayor habilidad para su manejo.
2 Derivar a la función 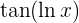
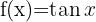 , y
, y 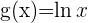 , para que de esta manera ya podamos aplicar la regla de la cadena, veamos:
, para que de esta manera ya podamos aplicar la regla de la cadena, veamos: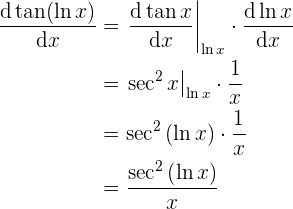
y entonces ya tenemos a la derivada de la función
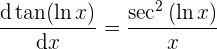
observe que en el proceso de derivación se fueron aplicando los pasos que se encuentran desglozados al principio.
3 Derivar a la función 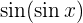
Identificamos a las funciones 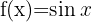 , y
, y 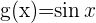 , como observamos ahora será menos complicado por lo simple de sus derivadas, veamos el desarrollo:
, como observamos ahora será menos complicado por lo simple de sus derivadas, veamos el desarrollo:
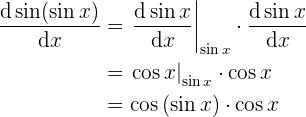
llegando al resultado buscado.
4 Derivar a la función 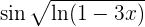
Aquí observamos que existe mas de una composición, para poder derivar a la función, lo que haremos será aplicar la regla de la cadena en diversas ocasiones hasta terminar de derivar.
Comencemos suponiendo que 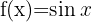 y
y 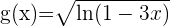 , entonces apliquemos la regla de la cadena
, entonces apliquemos la regla de la cadena

nos damos cuenta con esto, que ahora es necesario aplicar la regla de la cadena para

así que hagámoslo y posteriormente agregamos el resultado a la derivada original
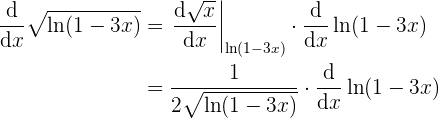
llevándonos así, a que ahora debemos aplicar regla de la cadena nuevamente

y entonces ya con esto podemos juntar todos los resultados
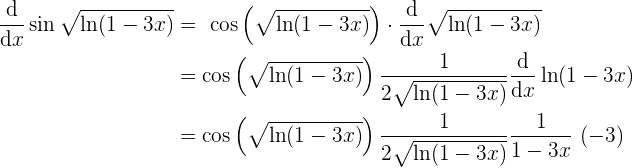
para que de esta forma ya podamos concluir que
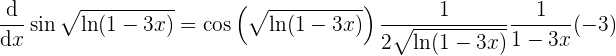
5 Derivar a la función 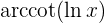
Nuevamente, identificamos a las funciones  y
y 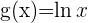 , para que de esta manera nos sea posible aplicar la regla de la cadena
, para que de esta manera nos sea posible aplicar la regla de la cadena
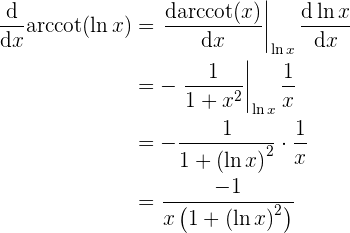
donde ahora podemos concluir que
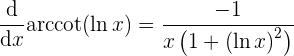
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Quería solo advertir que el gráfico de la diferencial tiene el ángulo de la recta tangente con β y analíticamente está indicado con α. Saludos.
hola gracias por tu observación, pero si el artículo es de «interpretación de la derivada» es el mismo ángulo pero con símbolo diferente.
cordial saludo sera que tu me puedes ayudar a resolver un ejercicio que es dada la función f(x)= X elevada a la 2/3 por entre paréntesis (xa la 2 -8) hallar los valores de X para los cuales esta crece te lo agradecería mucho
La descripcion es erronea donde da la derivada de arcocotangente, ya que dice derivada de arcotangete, se comieron el co, lo que puede llevar a confunciones, como en mi caso que pense que era la derivada de la inversa de tangente, cuando era la derivada de la inversa de cotangente.
Hola entendemos la confusión, pero como sabes en cada lugar toman la notación en forma diferente, en este caso se tomo arccot(x) donde se repite la c para diferenciar de arctan(x).
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Medio tarde me parece mi respuesta, pero simplemente tenes que derivar cada termino independientemente:
7^4=(7.4)^3
e^x-4=e^x-4 (por formula)
lnx=1/x
100=0 (Derivando una constante en terminos de x)
Hola podrías hacernos el favor de mostrarnos la función para dar una mejor explicación.