¡Bienvenidos a esta serie de ejercicios de aplicaciones de la derivada! en donde exploraremos cómo utilizar la derivada, una herramienta fundamental en cálculo, para resolver una variedad de problemas del mundo real. Las derivadas nos permiten entender cómo cambian las funciones en función de una variable y son esenciales en campos como la física, la economía, la biología y muchas otras disciplinas.
¡Prepárate para poner en práctica tus habilidades matemáticas y explorar cómo las derivadas pueden ayudarnos a comprender y resolver máximos y mínimos!
Encuentra los intervalos de crecimiento y de decrecimiento de la siguiente función:
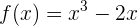
Notemos, primero, que el dominio de  es
es
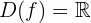
Para encontrar los intervalos de crecimiento, debemos encontrar esos intervalos donde la derivada es positiva. De manera similar, para encontrar los intervalos de decrecimiento, necesitamos encontrar los intervalos en donde la derivada es negativa. Por lo tanto, lo primero que debemos hacer es derivar la función:
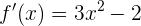
Ahora, para encontrar los intervalos donde  es positiva o negativa, debemos encontrar los ceros de
es positiva o negativa, debemos encontrar los ceros de  primero:
primero:
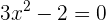
Por lo tanto, 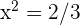 , de donde se sigue que
, de donde se sigue que 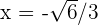 y
y 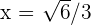 .
.
La lógica que seguimos aquí es que  cambia de signo alrededor de sus raíces o puntos de indeterminación.
cambia de signo alrededor de sus raíces o puntos de indeterminación.
Observemos que si 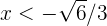 (es decir,
(es decir,  ), entonces
), entonces 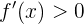 . Para notarlo evaluamos, por ejemplo, en
. Para notarlo evaluamos, por ejemplo, en  con lo que obtenemos
con lo que obtenemos 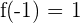 .
.
Similarmente, si 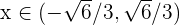 , entonces
, entonces 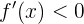 .
.
Por último, si  , entonces tenemos que
, entonces tenemos que 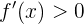 .
.
De este modo, los intervalos donde  es creciente son
es creciente son
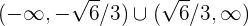
mientras que los intervalos donde  es decreciente son
es decreciente son
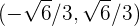
Encuentra los intervalos de crecimiento y de decrecimiento de la siguiente función:
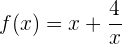
Notemos, primero, que el dominio de  es
es
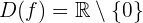
ya que tenemos una indeterminación en 0.
Para encontrar los intervalos de crecimiento, debemos encontrar esos intervalos donde la derivada es positiva. De manera similar, para encontrar los intervalos de decrecimiento, necesitamos encontrar los intervalos en donde la derivada es negativa. Por lo tanto, lo primero que debemos hacer es derivar la función:

Ahora, para encontrar los intervalos donde  es positiva o negativa, debemos encontrar los ceros de
es positiva o negativa, debemos encontrar los ceros de  primero:
primero:

Por lo tanto, 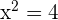 , de donde se sigue que
, de donde se sigue que  y
y  . Además, observemos que debemos tomar en cuenta el valor de
. Además, observemos que debemos tomar en cuenta el valor de  ya que
ya que  tiene una indeterminación ahí.
tiene una indeterminación ahí.
La lógica que seguimos aquí es que  cambia de signo alrededor de sus raíces o puntos de indeterminación.
cambia de signo alrededor de sus raíces o puntos de indeterminación.
Observemos que si 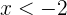 (es decir,
(es decir, 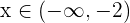 ), entonces
), entonces 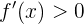 . Para notarlo evaluamos, por ejemplo, en
. Para notarlo evaluamos, por ejemplo, en  con lo que obtenemos
con lo que obtenemos 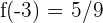 .
.
Similarmente, si 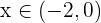 , entonces
, entonces 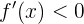 .
.
Si  , entonces
, entonces 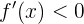 .
.
Por último, si 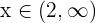 , entonces tenemos que
, entonces tenemos que 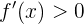 .
.
De este modo, los intervalos donde  es creciente son
es creciente son

mientras que los intervalos donde  es decreciente son
es decreciente son
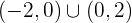
Encuentra los máximos y mínimos de la siguiente función:
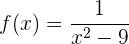
Para encontrar los máximos y mínimos de la función, necesitamos calcular la derivada de la función.

La función tendrá un máximo o mínimo cuando 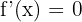 , es decir,
, es decir,
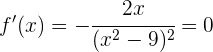
lo cual se cumple si 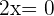 . Luego,
. Luego,  .
.
Para determinar si  es un máximo, podemos utilizar el criterio de la segunda derivada o el criterio de la primera derivada. En este caso, es más sencillo utilizar el criterio de la primera derivada para evitar calcular la segunda derivada. Para esto, evaluamos
es un máximo, podemos utilizar el criterio de la segunda derivada o el criterio de la primera derivada. En este caso, es más sencillo utilizar el criterio de la primera derivada para evitar calcular la segunda derivada. Para esto, evaluamos  en un punto a la izquierda de
en un punto a la izquierda de  y en un punto a la derecha de este (siempre que no sea -3 y 3). Como -1 está a la izquierda de
y en un punto a la derecha de este (siempre que no sea -3 y 3). Como -1 está a la izquierda de  , evaluamos:
, evaluamos:
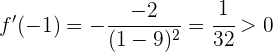
Asimismo, como 1 está a la derecha de  , entonces evaluamos:
, entonces evaluamos:
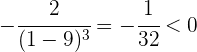
Notemos que a la izquierda de  la derivada es positiva (la función crece) y a la derecha de
la derivada es positiva (la función crece) y a la derecha de  la derivada es negativa (la función decrece).
la derivada es negativa (la función decrece).
El valor de  en
en  es:
es:
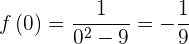
Esto significa que 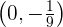 es un máximo (y el único valor extremo de
es un máximo (y el único valor extremo de  ).
).
Encuentra los máximos y mínimos de la siguiente función:

Para encontrar los máximos y mínimos de la función, necesitamos calcular la derivada de la función.
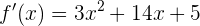
La función tendrá un máximo o mínimo cuando 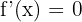 , es decir,
, es decir,

lo cual se cumple si  .
.
Para determinar si 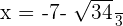 es un máximo, podemos utilizar el criterio de la segunda derivada o el criterio de la primera derivada. En este caso, es más sencillo utilizar el criterio de la primera derivada para evitar calcular la segunda derivada. Para esto, evaluamos
es un máximo, podemos utilizar el criterio de la segunda derivada o el criterio de la primera derivada. En este caso, es más sencillo utilizar el criterio de la primera derivada para evitar calcular la segunda derivada. Para esto, evaluamos  en un punto a la izquierda de
en un punto a la izquierda de 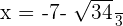 y en un punto a la derecha de este. Como -6 está a la izquierda de
y en un punto a la derecha de este. Como -6 está a la izquierda de  , evaluamos:
, evaluamos:
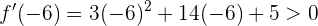
Asimismo, como -4 está a la derecha de  , entonces evaluamos:
, entonces evaluamos:
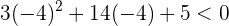
Notemos que a la izquierda de  la derivada es positiva (la función crece) y a la derecha de
la derivada es positiva (la función crece) y a la derecha de  la derivada es negativa (la función decrece).
la derivada es negativa (la función decrece).
El valor de  en
en  es:
es:
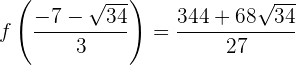
Esto significa que 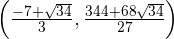 es un máximo de
es un máximo de  ).
).
Para determinar si 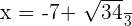 es un mínimo, podemos utilizar el criterio de la segunda derivada o el criterio de la primera derivada. En este caso, es más sencillo utilizar el criterio de la primera derivada para evitar calcular la segunda derivada. Para esto, evaluamos
es un mínimo, podemos utilizar el criterio de la segunda derivada o el criterio de la primera derivada. En este caso, es más sencillo utilizar el criterio de la primera derivada para evitar calcular la segunda derivada. Para esto, evaluamos  en un punto a la izquierda de
en un punto a la izquierda de 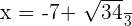 y como vimos previamente,
y como vimos previamente,  .
.
Asimismo, como 2 está a la derecha de  , entonces evaluamos:
, entonces evaluamos:
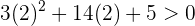
Notemos que a la izquierda de  la derivada es negativa (la función decrece) y a la derecha de
la derivada es negativa (la función decrece) y a la derecha de  la derivada es positiva (la función crece).
la derivada es positiva (la función crece).
El valor de  en
en  es:
es:

Esto significa que 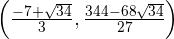 es un mínimo de
es un mínimo de  ).
).
Encuentra los máximos y mínimos de la siguiente función:
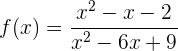
Para encontrar los máximos y mínimos de la función, necesitamos calcular la derivada de la función. Observemos, antes que el denominador es un trinomio cuadrado perfecto, por lo que la función se puede simplificar como

Así, la derivada es:
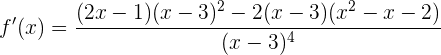
que al simplificar el numerador, obtenemos:
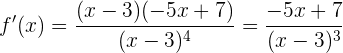
La función tendrá un máximo o mínimo cuando 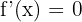 , es decir,
, es decir,
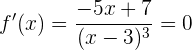
lo cual se cumple si 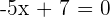 . Luego,
. Luego, 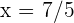 .
.
Para determianr si 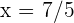 es un máximo, podemos utilizar el criterio de la segunda derivada o el criterio de la primera derivada. En este caso, es más sencillo utilizar el criterio de la primera derivada para evitar calcular la segunda derivada. Para esto, evaluamos
es un máximo, podemos utilizar el criterio de la segunda derivada o el criterio de la primera derivada. En este caso, es más sencillo utilizar el criterio de la primera derivada para evitar calcular la segunda derivada. Para esto, evaluamos  en un punto a la izquierda de
en un punto a la izquierda de 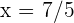 y en un punto a la derecha de este (siempre que no sea mayor a 3). Como 1 está a la izquierda de
y en un punto a la derecha de este (siempre que no sea mayor a 3). Como 1 está a la izquierda de  , evaluamos:
, evaluamos:

Asimismo, como 2 está a la derecha de  , entonces evaluamos:
, entonces evaluamos:
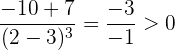
Notemos que a la izquierda de  la derivada es negativa (la función decrece) y a la derecha de
la derivada es negativa (la función decrece) y a la derecha de  la derivada es positiva (la función crece).
la derivada es positiva (la función crece).
El valor de  en
en  es:
es:

Esto significa que 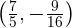 es un mínimo (y el único valor extremo de
es un mínimo (y el único valor extremo de  ).
).
Determina las ecuaciones de la recta tangente y la ecuación normal en  de la siguiente función:
de la siguiente función:
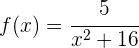
La primera derivada está dada por
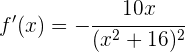
La pendiente de la recta tangente en  está dada por
está dada por

La función en  es
es

Por tanto, la función pasa por el punto 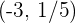 y la recta tangente debe pasar por el mismo punto.
y la recta tangente debe pasar por el mismo punto.
1 Para determinar ecuación de la recta tangente, utilizamos la fórmula punto pendiente con  y
y  :
:

por lo que la ecuación de la recta tangente es
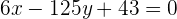
2 Similarmente, para encontrar la ecuación de la recta normal, utilizamos la fórmula pendiente, pero ahora con 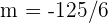 y
y  :
:
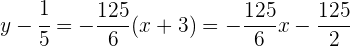
por lo que la ecuación de la recta normal es
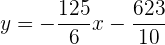
o

Determina las ecuaciones de la recta tangente y la ecuación normal en el punto de inflexión de la siguiente función:

Primero debemos encontrar el punto de inflexión de la derivada. Esto lo logramos al encontrar la segunda derivada de la función. La primera derivada está dada por

mientras que la segunda derivada está dada por
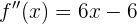
El punto de inflexión se encuentra cuando  , es decir,
, es decir,

por lo que  es el punto de inflexión.
es el punto de inflexión.
Luego, el valor de la derivada en el punto de inflexión es:
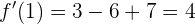
Así, la pendiente de  en
en  es 4. La recta tangente debe tener esa pendiente.
es 4. La recta tangente debe tener esa pendiente.
Si evaluamos la función en  , tenemos:
, tenemos:
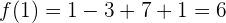
Por tanto, la función pasa por el punto 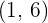 y la recta tangente debe pasar por el mismo punto.
y la recta tangente debe pasar por el mismo punto.
1 Para determinar ecuación de la recta tangente, utilizamos la fórmula punto pendiente con  y
y 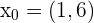 :
:
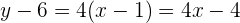
por lo que la ecuación de la recta tangente es
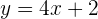
2 Similarmente, para encontrar la ecuación de la recta normal, utilizamos la fórmula pendiente, pero ahora con 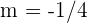 y
y 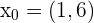 :
:
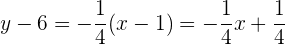
por lo que la ecuación de la recta normal es
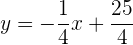
or
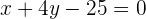
La cantidad  expresa el dinero acumulado en una máquina de tragaperras durante un día y se calcula de la siguiente manera:
expresa el dinero acumulado en una máquina de tragaperras durante un día y se calcula de la siguiente manera:
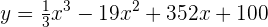
en donde la variable  representa el tiempo en horas (entre 0 y 24). Responde las siguientes preguntas:
representa el tiempo en horas (entre 0 y 24). Responde las siguientes preguntas:
a ¿Se queda sin dinero la máquina en alguna ocasión?
b Si se realiza la "caja" a las 24 horas. ¿La máquina da ganancias a los dueños de la máquina?
c ¿A qué hora la recaudación es máxima y a qué hora es mínima?
d ¿En qué momento la máquina entrega el mayor premio?
a ¿Se queda sin dinero la máquina en alguna ocasión?
Para responder esta pregunta, es necesario verificar que 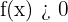 para todo
para todo 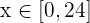 . Esto no es sencillo, pues tenemos que encontrar las raíces de
. Esto no es sencillo, pues tenemos que encontrar las raíces de  y es una ecuación de tercer grado. La forma más sencilla es graficar la función:
y es una ecuación de tercer grado. La forma más sencilla es graficar la función:

Observemos que la grafica es positiva en todo el intervalo 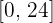 . Asimismo, observemos que toma valores muy grandes, incluso superiores a
. Asimismo, observemos que toma valores muy grandes, incluso superiores a 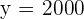 .
.
Por lo tanto, podemos concluir que la máquina nunca se queda sin monedas.
b Si se realiza la "caja" a las 24 horas. ¿La máquina da ganancias a los dueños de la máquina?
Para responder esta pregunta debemos determinar la cantidad de dinero al inicio y al final del periodo de 24 horas. Es decir, 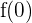 y
y 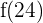 . Tenemos que
. Tenemos que
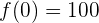
y
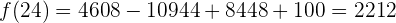
por lo tanto, al final de las 24 horas, la máquina tiene 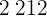 euros. Esto representa una ganacia de
euros. Esto representa una ganacia de 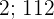 euros por día.
euros por día.
c ¿A qué hora la recaudación es máxima y a qué hora es mínima?
Interpretamos los momentos de mayor y menor recaudación como aquellos momentos donde la máquina tiene el mayor o menor dinero.
De la gráfica podemos observar que la máquina tiene el menor dinero cuando  , pues es el único caso donde
, pues es el único caso donde 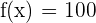 . Este mínimo no se puede obtener por medio de la derivada.
. Este mínimo no se puede obtener por medio de la derivada.
Para la mayor recaudación debemos encontrar el máximo de la función. Por tanto, debemos derivar:
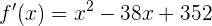
Encontramos las raíces por medio de la fórmula general:
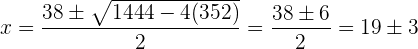
por lo que las raíces son 16 y 22.
Calculamos la segunda derivada:
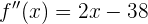
y observamos que  por lo que en
por lo que en  tenemos un máximo. Al evaluar
tenemos un máximo. Al evaluar 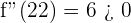 , por lo que
, por lo que  es un mínimo local (sin embargo, su valor es mayor al de
es un mínimo local (sin embargo, su valor es mayor al de 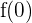 .
.
Antes de concluir que el momento de máxima recaudación es  , debemos comprobar que
, debemos comprobar que 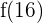 sea mayor a
sea mayor a 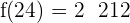 :
:
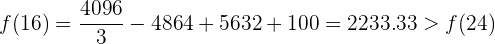
por lo que, en efecto, el momento de mayor recaudación es cuando  . Es decir, a la 16va hora.
. Es decir, a la 16va hora.
d ¿En qué momento la máquina entrega el mayor premio?
El mayor premio se entrega cuando  decrece lo mayor posible. La función solo decrece entre 16 y 22, así que en alguno de estos momentos se entrega el mayor premio. Hay dos formas de encontrarlo, una forma es encontrar el mínimo de
decrece lo mayor posible. La función solo decrece entre 16 y 22, así que en alguno de estos momentos se entrega el mayor premio. Hay dos formas de encontrarlo, una forma es encontrar el mínimo de  el cual, al ser una parábola, será el punto medio de sus raíces (16 y 22), es decir, 19.
el cual, al ser una parábola, será el punto medio de sus raíces (16 y 22), es decir, 19.
Otra forma es encontrar el punto de inflexión utilizando la segunda derivada. En este caso, 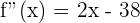 . Si igualamos a 0, obtenemos
. Si igualamos a 0, obtenemos

de manera que 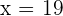 . Justo como lo habíamos calculado anteriormente. Por consiguiente, en la hora 19 se entrega el mayor premio.
. Justo como lo habíamos calculado anteriormente. Por consiguiente, en la hora 19 se entrega el mayor premio.
Sea 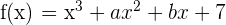 . Encuentra los valores de
. Encuentra los valores de  y
y  de manera que la gráfica de la función de
de manera que la gráfica de la función de  tenga un punto de inflexión en
tenga un punto de inflexión en  y cuya recta tangente en ese punto forme un ángulo de
y cuya recta tangente en ese punto forme un ángulo de 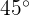 con el eje-x
con el eje-x
Para encontrar el punto de inflexión necesitamos la segunda derivada. Por tanto, empezamos calculando la primera derivada:
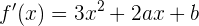
Luego, la segunda derivada es

Como queremos que el punto de inflexión esté en  , evaluamos en 1 e igualamos a 0:
, evaluamos en 1 e igualamos a 0:
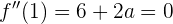
de donde se obtiene la ecuación 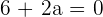 y, por tanto,
y, por tanto,  . Luego, deseamos que la tangente en ese punto forme un ángulo de
. Luego, deseamos que la tangente en ese punto forme un ángulo de 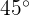 con el eje-x. Sabemos que la tangente de ese ángulo es la pendiente, por tanto
con el eje-x. Sabemos que la tangente de ese ángulo es la pendiente, por tanto

es decir, la recta tangente debe tener una pendiente de 1, es decir, 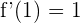 . Así, evaluando en la derivada, obtenemos
. Así, evaluando en la derivada, obtenemos
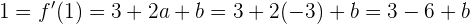
De donde obtenemos que 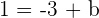 o
o  .
.
Por lo tanto,  y
y  .
.
Obtén la ecuación de la tangente a la gráfica de 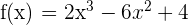 en su punto de inflexión
en su punto de inflexión
Primero debemos encontrar el punto de inflexión. Para hacerlo, necesitamos que la segunda derivada sea igual a cero. Primero calculamos la primera derivada:
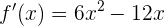
Por lo que la segunda derivada es
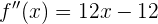
Así, al igualar en cero tenemos 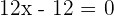 o
o  . Por lo que el punto de inflexión se encuentra cuando
. Por lo que el punto de inflexión se encuentra cuando  . Ahora evaluamos
. Ahora evaluamos  en
en  :
:
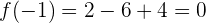
de manera que el punto de inflexión es el punto  .
.
Asimismo, la recta tangente tiene como pendiente a 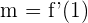 . Por tanto, evaluamos
. Por tanto, evaluamos  en
en  :
:
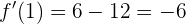
Con esto ya podemos encontrar la ecuación de la recta tangente utilizando la fórmula punto-pendiente:
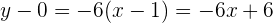
Así, la ecuación de la recta tangente es

Determina el  ,
,  y
y  para que la función
para que la función 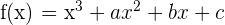 tenga un máximo en
tenga un máximo en 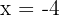 , tenga un mínimo para
, tenga un mínimo para  y tome el valor de 1 en
y tome el valor de 1 en 
Como sabemos donde están los máximos y mínimos, necesitamos la primera derivada de la función:
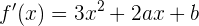
donde los valores críticos deben estar en 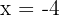 y
y  (nota que no importa si son mínimos o máximos, como el coeficiente principal es 1, entonces el máximo siempre estará a la izquierda). Así, se debe cumplir que
(nota que no importa si son mínimos o máximos, como el coeficiente principal es 1, entonces el máximo siempre estará a la izquierda). Así, se debe cumplir que 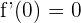 y
y 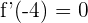 :
:
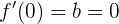
de donde se sigue que  . Similarmente,
. Similarmente,
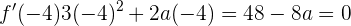
de donde se obtiene que  al despejar
al despejar  .
.
Por último, sabemos que 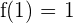 . Así:
. Así:
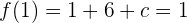
Por lo que 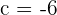 . Así, los valores son
. Así, los valores son
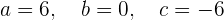
y la función es 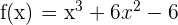 .
.
Determinar  ,
,  ,
,  ,
,  y
y  de manera que la curva
de manera que la curva 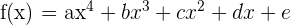 tenga un punto crítico en
tenga un punto crítico en  y tenga un punto de inflexión tangente a la recta
y tenga un punto de inflexión tangente a la recta  en el punto
en el punto 
Sabemos que  tiene un punto de inflexión en
tiene un punto de inflexión en  , esto significa que
, esto significa que
1  debe pasar por el punto
debe pasar por el punto  :
:

por lo tanto, 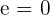 .
.
2 La segunda derivada de  debe ser 0 en
debe ser 0 en  . Por tanto, calculamos las derivadas:
. Por tanto, calculamos las derivadas:
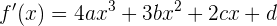
y

donde se debe cumplir que 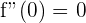 :
:
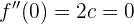
de donde se sigue que 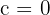 .
.
Todavía nos faltan por determinar las constantes  ,
,  y
y  . Sin embargo, ya sabemos que la función tiene la forma
. Sin embargo, ya sabemos que la función tiene la forma
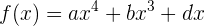
Sabemos que la función es tangente a  (pendiente 2) en el punto
(pendiente 2) en el punto  . Por tanto, debemos tener que
. Por tanto, debemos tener que 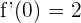 :
:
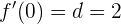
de donde se sigue de inmediato que  .
.
Por último, sabemos que  tiene un punto crítico en
tiene un punto crítico en  . Esto significa que
. Esto significa que
1  pasa por el punto
pasa por el punto  o que
o que 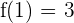 . Así:
. Así:
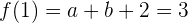
o

2 La derivada de  en
en  debe ser 0. Es decir:
debe ser 0. Es decir:
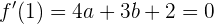
o
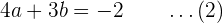
Notemos que (1) y (2) forman un sistema de ecuaciones. Una forma de resolverlo es multiplicar a (1) por 3 y restar el resultado a (2). Esto resulta:
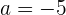
Luego, sustituimos este valor en (1) para obtener  o
o  .
.
Por tanto,
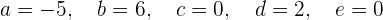
La curva 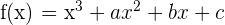 corta al eje de abscisas en
corta al eje de abscisas en  y tiene un punto de inflexión en
y tiene un punto de inflexión en 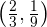 . Encuentra los valores de
. Encuentra los valores de  ,
,  y
y 
Como la curva corta al eje de abscisas en  , entonces debemos tener que
, entonces debemos tener que  . Es decir,
. Es decir,
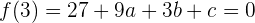
o

Luego, conocemos un punto de inflexión de  . Esto significa dos cosas:
. Esto significa dos cosas:
1  debe pasar por el punto
debe pasar por el punto 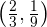

es decir
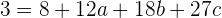
o

2 Además, sabemos que el punto de inflexión está en 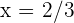 . Por lo tanto, necesitamos la segunda derivada de
. Por lo tanto, necesitamos la segunda derivada de  . Primero calculamos la primera derivada:
. Primero calculamos la primera derivada:
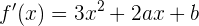
por lo que la segunda derivada es

donde sabemos que 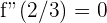 , es decir
, es decir
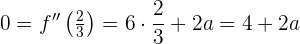
Luego,  .
.
Ahora sustituimos  en las dos ecuaciones anteriores. Al sustituir en (2) tenemos
en las dos ecuaciones anteriores. Al sustituir en (2) tenemos  , es decir
, es decir
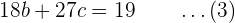
y al sustituir en (1), obtenemos 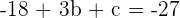 , es decir,
, es decir,

Sustituyendo en la ecuación (3), se obtiene que
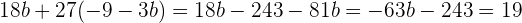
es decir, 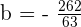 . Luego, al sustituir en la expresión que tenemos para
. Luego, al sustituir en la expresión que tenemos para  , obtenemos
, obtenemos
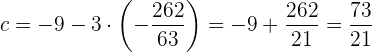
Por lo tanto, los valores son
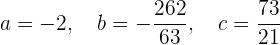
Dada la función
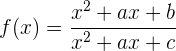
encuentra los valores de  ,
,  y
y  tales que la función
tales que la función  tenga en
tenga en  un extremo local y que la curva pase por el origen de coordenadas
un extremo local y que la curva pase por el origen de coordenadas
Deseamos que la curva pase por el origen de coordenadas. Es decir,  . Si evaluamos la función en el origen, obtenemos:
. Si evaluamos la función en el origen, obtenemos:
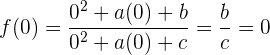
de donde se sigue  y que
y que  . Por lo tanto, ya encontramos uno de los tres valores.
. Por lo tanto, ya encontramos uno de los tres valores.
Asimismo, sabemos que  debe tener un extremo local en
debe tener un extremo local en  . Esto significa dos cosas:
. Esto significa dos cosas:
1 Lo primero, es que 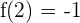 . Es decir,
. Es decir,  debe pasar por el punto
debe pasar por el punto  . De modo que, al evaluar
. De modo que, al evaluar  en 2, obtenemos
en 2, obtenemos

Si pasamos el denominador multiplicando, obtenemos
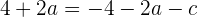
es decir

2 Además de que  deba pasar por
deba pasar por  , también se debe cumplir que
, también se debe cumplir que 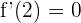 para que la función tenga un extremo local en ese punto. Por tanto, debemos encontrar la derivada de
para que la función tenga un extremo local en ese punto. Por tanto, debemos encontrar la derivada de  utilizando la regla del cociente:
utilizando la regla del cociente:
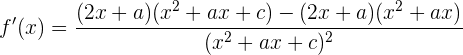
que, si simplificamos un poco, resulta en

Al evaluar en 2, obtenemos:
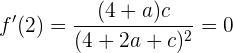
Debemos tener que 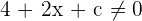 para que no se indetermine la derivada. Así, la expresión es equivalente a
para que no se indetermine la derivada. Así, la expresión es equivalente a 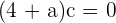 . Como sabemos que
. Como sabemos que  , entonces se debe tener que
, entonces se debe tener que 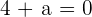 . Así,
. Así, 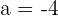 .
.
Luego, sustituyendo en la ecuación del caso anterior, tenemos:
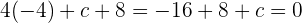
es decir 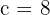 .
.
Por lo tanto, 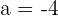 ,
, 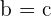 y
y 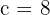 .
.
Encuentra los valores de  y
y  para que la función
para que la función 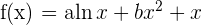 tenga valores extremos en los puntos
tenga valores extremos en los puntos 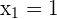 y
y  . Luego, dados esos valores de
. Luego, dados esos valores de  y
y  , ¿qué tipo de extremos tiene la función en
, ¿qué tipo de extremos tiene la función en  y en
y en  ?
?
Como queremos que la función tenga valores extremos en 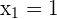 y
y  , entonces debemos tener que
, entonces debemos tener que  y
y 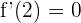 .
.
Por lo tanto, primero calculamos la derivada de la función
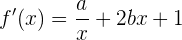
Ahora evaluamos en 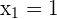 :
:
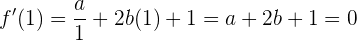
Asimismo, si evaluamos  :
:
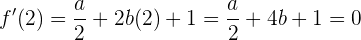
Por tanto, tenemos el siguiente sistema de ecuaciónes
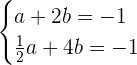
cuya solución es  y
y  . Por tanto, los valores son
. Por tanto, los valores son

y nuestra función es
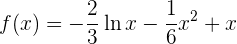
Luego, para determinar si son mínimos o máximos, calculamos la segunda derivada:

Si evaluamos en 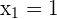 :
:
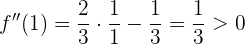
por lo que tenemos un mínimo en 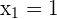 . Similarmente, si evaluamos en
. Similarmente, si evaluamos en  :
:
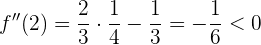
de manera que tenemos un máximo en  .
.
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
cordial saludo sera que tu me puedes ayudar a resolver un ejercicio que es dada la función f(x)= X elevada a la 2/3 por entre paréntesis (xa la 2 -8) hallar los valores de X para los cuales esta crece te lo agradecería mucho
La descripcion es erronea donde da la derivada de arcocotangente, ya que dice derivada de arcotangete, se comieron el co, lo que puede llevar a confunciones, como en mi caso que pense que era la derivada de la inversa de tangente, cuando era la derivada de la inversa de cotangente.
Hola entendemos la confusión, pero como sabes en cada lugar toman la notación en forma diferente, en este caso se tomo arccot(x) donde se repite la c para diferenciar de arctan(x).
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Medio tarde me parece mi respuesta, pero simplemente tenes que derivar cada termino independientemente:
7^4=(7.4)^3
e^x-4=e^x-4 (por formula)
lnx=1/x
100=0 (Derivando una constante en terminos de x)
Excelente contenido. Creo es posible mejorar el contenido para que sea más didáctico con más ejemplos, partiendo de lo elemental a lo complejo, para que el texto pueda ser más entendible para estudiantes de secundaria en Costa Rica.
Excelente artículo y muy dinámico.
Agradecemos tu comentario, la verdad estamos trabajando mucho para lograr tener las mejores explicaciones para que sea mas entendible al publico y para ello lo que ustedes recomienden nos ayuda en gran forma, esperamos que en un futuro seamos mejores siguiendo sus sugerencias, otra vez gracias.
Hola podrías hacernos el favor de mostrarnos la función para dar una mejor explicación.