Si 
y 
son funciones inversas, es decir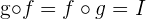 
. Entonces
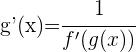
Los/las mejores profesores/as de Matemáticas que están disponibles
Amin
15€
/h
¡1a clase gratis!
Francisco javier
17€
/h
¡1a clase gratis!
Agustina
25€
/h
¡1a clase gratis!
Jose
18€
/h
¡1a clase gratis!
Antonio c
14€
/h
¡1a clase gratis!
Pedro
15€
/h
¡1a clase gratis!
Santiago
18€
/h
¡1a clase gratis!
Viviana
25€
/h
¡1a clase gratis!
Amin
15€
/h
¡1a clase gratis!
Francisco javier
17€
/h
¡1a clase gratis!
Agustina
25€
/h
¡1a clase gratis!
Jose
18€
/h
¡1a clase gratis!
Antonio c
14€
/h
¡1a clase gratis!
Pedro
15€
/h
¡1a clase gratis!
Santiago
18€
/h
¡1a clase gratis!
Viviana
25€
/h
¡1a clase gratis!
Pasos para derivar una función
a partir de su función inversa, podemos seguir los siguientes pasos: 1 Buscamos la función inversa de , que escribiremos de la forma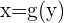 
.
2 Hacemos 
.
3 Usando lo anterior, 
.
4 Sustituimos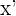 
por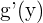 
y operamos.
5 Por último sustituimos 
por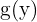 
y habremos acabado.
Ejemplos usando la derivada de la función inversa
1 Derivar, usando la derivada de la función inversa: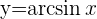 
La función inversa de la dada es: 
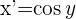
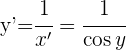
Sabiendo que , se tiene:
2 Derivar, usando la derivada de la función inversa: 
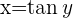
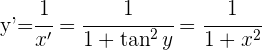
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
cordial saludo sera que tu me puedes ayudar a resolver un ejercicio que es dada la función f(x)= X elevada a la 2/3 por entre paréntesis (xa la 2 -8) hallar los valores de X para los cuales esta crece te lo agradecería mucho
La descripcion es erronea donde da la derivada de arcocotangente, ya que dice derivada de arcotangete, se comieron el co, lo que puede llevar a confunciones, como en mi caso que pense que era la derivada de la inversa de tangente, cuando era la derivada de la inversa de cotangente.
Hola entendemos la confusión, pero como sabes en cada lugar toman la notación en forma diferente, en este caso se tomo arccot(x) donde se repite la c para diferenciar de arctan(x).
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Medio tarde me parece mi respuesta, pero simplemente tenes que derivar cada termino independientemente:
7^4=(7.4)^3
e^x-4=e^x-4 (por formula)
lnx=1/x
100=0 (Derivando una constante en terminos de x)
Excelente contenido. Creo es posible mejorar el contenido para que sea más didáctico con más ejemplos, partiendo de lo elemental a lo complejo, para que el texto pueda ser más entendible para estudiantes de secundaria en Costa Rica.
Excelente artículo y muy dinámico.
Agradecemos tu comentario, la verdad estamos trabajando mucho para lograr tener las mejores explicaciones para que sea mas entendible al publico y para ello lo que ustedes recomienden nos ayuda en gran forma, esperamos que en un futuro seamos mejores siguiendo sus sugerencias, otra vez gracias.
Hola podrías hacernos el favor de mostrarnos la función para dar una mejor explicación.