Ejercicios propuestos
Dada la ecuación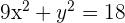 
, hallar la ecuación de la recta tangente que sea paralela a la recta de ecuación 
.
Supongamos que 
es el punto de tangencia, además conviene saber la pendiente que tiene que tener la recta tangente a la curva.
Sabemos que la recta tangente es paralela a la recta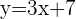 
por lo tanto tendrán la misma pendiente.
Ahora tenemos que encontrar en que punto de la curva dada la pendiente es igual a 
, y para ello derivamos implicitamente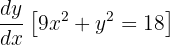
entonces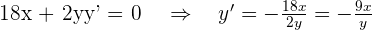 
Puesto que la pendiente es tres, entonces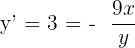 
Sustituyendo el punto de tangencia : 
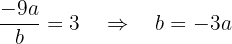y se tiene que cumplir el siguiente sistema 
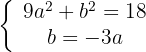de donde obtenemos que los posibles puntos son 
Con estos puntos y la pendiente, obtenemos dos ecuaciones que cumplen con lo que buscamos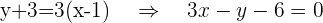 
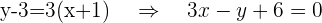
Hallar el área del triángulo determinado por los ejes de coordenadas y la tangente a la curva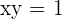 
en el punto 
.
Si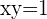 
, entonces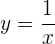 
La pendiente de la recta tangente a la curva está dada por la derivada
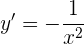
Evaluamos para obtener la pendiente en 
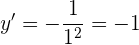
La ordenada del punto se obtiene evaluando en la función original
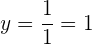
Finalmente
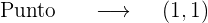
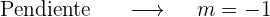
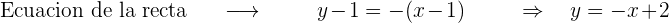
Intersección con el eje OX
Un vértice es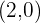 
Intersección con el eje OY
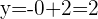
Otro vértice es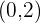 
Y la figura es como a continuación
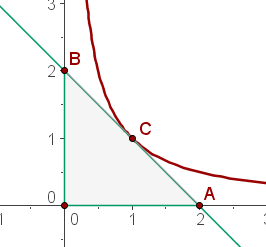
Como es un triángulo rectángulo, su base y altura están dados por los catetos, que en este caso ambos miden 
. El área es
La ecuación de un movimiento rectilíneo es: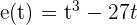
. ¿En qué momento la velocidad en nula? Hallar la aceleración en ese instante.
La ecuación de movimiento rectilíneo que se nos da es: 
.
Recordemos que la velocidad es la primer derivada de la función de movimiento, por lo tanto, para encontrar el momento en el cual la velocidad es nula, debemos derivar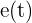 
, igualar a cero y despejar 
:
.
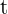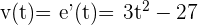Igualando a 
y despejando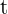
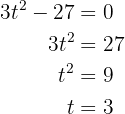
Así, cuando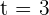 
, la velocidad es nula.
Ahora, la aceleración es igual a la derivada de la velocidad (o segunda derivada del movimiento), por lo tanto, para encontrar la aceleración en el tiempo en el cual la velocidad es nula (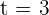
), debemos derivar 
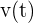y evaluar en :
,
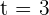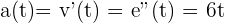evaluando en 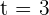, tenemos
.
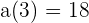Un productor de nueces estima, de la experiencia de los años anteriores, que si se plantan 
árboles por hectárea, cada árbol producirá en promedio 
kilos de nueces cada año. Si por cada árbol adicional que se planta por hectárea la producción promedio por árbol desciende 
kilo, ¿cuántos árboles debe plantar para maximizar la producción por hectárea? ¿Cuál es esa producción máxima?
Sea
: numero de arboles adicionales
: Producción por hectárea
entonces 
Derivando y resolviendo la ecuación que proporciona la primera derivada igual a cero obtenemos los puntos críticos: 
Luego 
proporciona el máximo, con un número de árboles de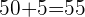 
y una producción por hectárea que obtenemos sustituyendo el valor 
en :
Calcular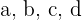 
de la función 
para que tenga un vértice en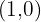 
y un punto de inflexión en 
.
Puesto que tenemos un vértice en 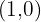entonces: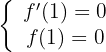
Otro dato es que tenemos un punto de inflexión en , entonces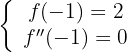 
Con lo anterior obtenemos el siguiente sistema de ecuaciones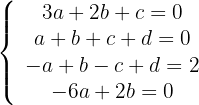 
lo resolvemos y obtenemos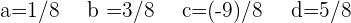 
Halla el número positivo cuya suma con veinticinco veces su inverso sea mínima.
Llamemos al número que buscamos. El cual debe ser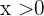 
.
Para encontrar lo tenemos que minimizar la función: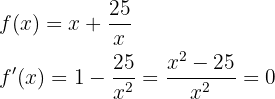 
entonces 
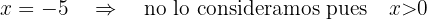
Por tanto, el número buscado es y el mínimo es 
.
De entre todos los triángulos rectángulos cuyos catetos tienen longitudes que suman cm, hallar las dimensiones de aquel cuya área es máxima.
Tenemos que 
Entonces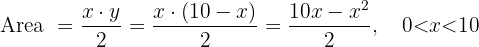
Tenemos que maximizar la función: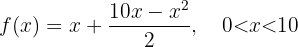 
Derivando 
Por lo tanto, los catetos miden 
cm cada uno y el área máxima es de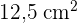 
.
Sabemos que la función 
pasa por el punto 
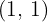y en ese punto tiene tangente paralela a la recta 
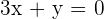. Hallar 
y 
Tenemos que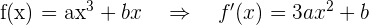
y de la información proporcionada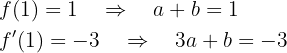 
Resolviendo obtenemos que 
y 
.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La descripcion es erronea donde da la derivada de arcocotangente, ya que dice derivada de arcotangete, se comieron el co, lo que puede llevar a confunciones, como en mi caso que pense que era la derivada de la inversa de tangente, cuando era la derivada de la inversa de cotangente.
Hola entendemos la confusión, pero como sabes en cada lugar toman la notación en forma diferente, en este caso se tomo arccot(x) donde se repite la c para diferenciar de arctan(x).
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Medio tarde me parece mi respuesta, pero simplemente tenes que derivar cada termino independientemente:
7^4=(7.4)^3
e^x-4=e^x-4 (por formula)
lnx=1/x
100=0 (Derivando una constante en terminos de x)
Excelente contenido. Creo es posible mejorar el contenido para que sea más didáctico con más ejemplos, partiendo de lo elemental a lo complejo, para que el texto pueda ser más entendible para estudiantes de secundaria en Costa Rica.
Excelente artículo y muy dinámico.
Agradecemos tu comentario, la verdad estamos trabajando mucho para lograr tener las mejores explicaciones para que sea mas entendible al publico y para ello lo que ustedes recomienden nos ayuda en gran forma, esperamos que en un futuro seamos mejores siguiendo sus sugerencias, otra vez gracias.
Hola: El últipo ejercicio de aplicación me parece que es incorrecto ya que no está obteniendo la derivada del volumen del cono
Hola si te refieres al triángulo que gira, si se derivo el volumen, si estoy equivocado por favor indícamelo.