La derivada es una herramienta fundamental en el cálculo diferencial que describe cómo cambia una función en relación con sus variables independientes. En el contexto de la física, las derivadas permiten modelar y entender una amplia variedad de fenómenos, tales como el movimiento de los objetos, las variaciones de las magnitudes físicas en el tiempo, y los cambios de condiciones de los sistemas en el espacio.
En esta serie de ejercicios resueltos, nos enfocaremos en diversas aplicaciones físicas de la derivada, demostrando cómo este concepto es crucial para resolver problemas reales.
La relación entre la distancia recorrida en metros por un móvil y el tiempo en segundos es 
. Calcular:
a la velocidad media entre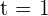 
y 
.
b La velocidad instantánea en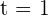 
.
a la velocidad media entre 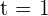y .
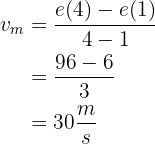
b La velocidad instantánea en .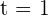
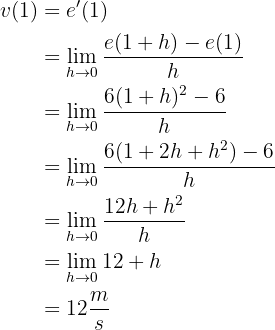
Debido a unas pésimas condiciones ambientales, una colonia de un millón de bacterias no comienza su reproducción hasta pasados dos meses. La función que representa la población de la colonia al variar el tiempo (expresado en meses) viene dada por:
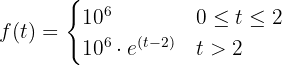
Se pide:
a Verificar que la población es función continua del tiempo.
b Calcular la tasa de variación media de la población en los intervalos 
y 
.
c Calcular la tasa de variación instantánea en .
a Verificar que la población es función continua del tiempo.
El único punto que debemos analizar es en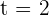 
. Notemos que
.
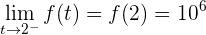Además
.
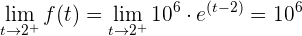Por lo tanto es continua.
b Calcular la tasa de variación media de la población en los intervalos y .
Primero hagamos el cálculo para el intervalo 
.
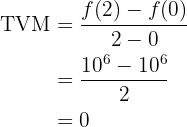Ahora hagamos el cálculo para el intervalo
.
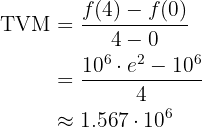c Calcular la tasa de variación instantánea en .
La derivada de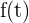 
está dada por
,
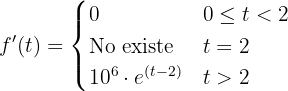por lo tanto
Una población bacteriana tiene un crecimiento dado por la función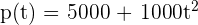 
, siendo 
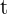el tiempo metido en horas. Se pide:
a La velocidad media de crecimiento.
b La velocidad instantánea de crecimiento.
c La velocidad de crecimiento instantáneo para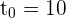 
horas.
a La velocidad media de crecimiento.
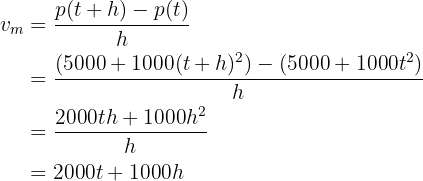
b La velocidad instantánea de crecimiento.
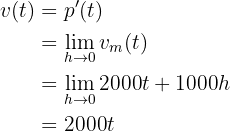
c La velocidad de crecimiento instantáneo para 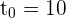horas.
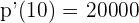
La ecuación de un movimiento rectilíneo es: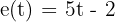 
. ¿Cuál es la velocidad instantánea en 
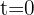y 
?
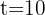La ecuación de movimiento rectilíneo que se nos da es: 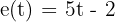. Recordemos que la velocidad es la primera derivada de la función de movimiento, por lo tanto, para encontrar la velocidad, debemos derivar 
:
.
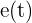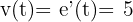Para encontrar la velocidad en los instantes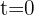 
y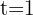 
basta con sustituir en la expresión de velocidad
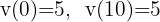
Así, tenemos que la velocidad es constante.
La ecuación de un movimiento rectilíneo es: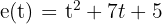 
. ¿Cuál es la velocidad instantánea en 
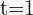y 
?
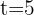La ecuación de movimiento rectilíneo que se nos da es: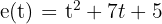 
. Recordemos que la velocidad es la primera derivada de la función de movimiento, por lo tanto, para encontrar la velocidad, debemos derivar :
.
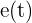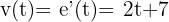Para encontrar la velocidad en los instantes 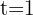y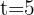 
basta con sustituir en la expresión de velocidad
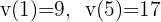
La ecuación de velocidad de un movimiento rectilíneo es: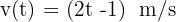 
. Hallar la aceleración en cualquier instante.
La ecuación de velocidad que se nos da es: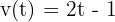 
. Recordemos que la aceleración es derivada de la función de velocidad, por lo tanto, debemos derivar 
:
.
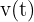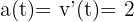Así, la aceleración es constante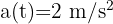 
.
La ecuación de un movimiento rectilíneo es: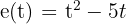 
. Hallar la aceleración en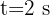 
La ecuación de movimiento que se nos da es: 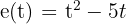. Recordemos que la velocidad es la derivada de la distancia y la aceleración es derivada de la función de velocidad, por lo tanto, debemos derivar 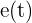dos veces :
.
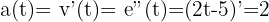Así, la aceleración es constante .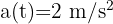
La ecuación de un movimiento rectilíneo es: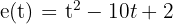 
. ¿En qué momento la velocidad en nula?
La ecuación de movimiento rectilíneo que se nos da es: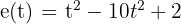 
. Recordemos que la velocidad es la primera derivada de la función de movimiento, por lo tanto, para encontrar el momento en el cual la velocidad es nula, debemos derivar 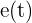, igualar a cero y despejar 
:
.
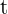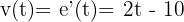Igualando a 
y despejando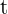
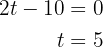
Así, cuando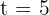 
, la velocidad es nula.
La ecuación de un movimiento rectilíneo es: 
. ¿En qué momento la velocidad en nula? Hallar la aceleración en ese instante.
La ecuación de movimiento rectilíneo que se nos da es: . Recordemos que la velocidad es la primera derivada de la función de movimiento, por lo tanto, para encontrar el momento en el cual la velocidad es nula, debemos derivar 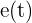, igualar a cero y despejar :
.
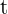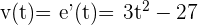Igualando a y despejando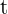
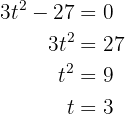
Así, cuando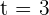 
, la velocidad es nula.
Ahora, la aceleración es igual a la derivada de la velocidad (o segunda derivada del movimiento), por lo tanto, para encontrar la aceleración en el tiempo en el cual la velocidad es nula (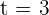
), debemos derivar 
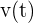y evaluar en :
,
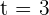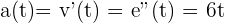evaluando en 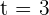, tenemos
.
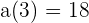La ecuación de un movimiento circular es: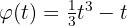 
. ¿Cuál es la velocidad angular al cabo de tres segundos?
Tenemos que la velocidad es la primer derivada de la función de movimiento, por lo tanto, para obtener la velocidad a los tres segundos, debemos obtener la derivada de 
y evaluar en .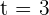
.
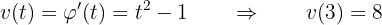La ecuación de un movimiento circular es: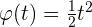 
. ¿Cuál es la velocidad y la aceleración angulares al cabo de siete segundos?
Tenemos que la velocidad es la primer derivada de la función de movimiento, por lo tanto, para obtener la velocidad a los siete segundos, debemos obtener la derivada de y evaluar en 
.
.
Ahora bien, la aceleración es la segunda derivada de la función de movimiento, por lo tanto, para obtener la aceleración a los siete segundos, debemos obtener la derivada de y evaluar en .
.
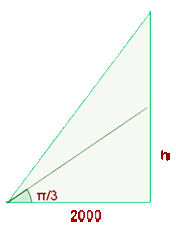
Un observador se encuentra a 
de lanzamiento de la torre de un cohete. Cuando éste despega verticalmente mide la variación del ángulo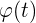 
que forma la línea visual que le une con el cohete y la del suelo horizontal en función del tiempo transcurrido. Sabiendo que 
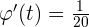, se pide:
a ¿Cuál es la altura del cohete cuando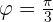 
radianes?
b ¿Cuál es la velocidad del cohete cuando 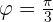radianes?
a ¿Cuál es la altura del cohete cuando 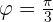radianes?
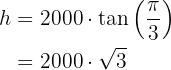
b ¿Cuál es la velocidad del cohete cuando 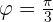radianes?
Debemos calcular la derivada de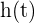 
para obtener la velocidad:
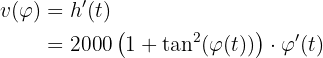
Por lo tanto
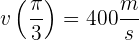
Se bombea gas a un globo esférico a razón de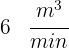 
. Si la presión se mantiene constante. ¿Cuál es la velocidad con la que cambia el radio del globo cuando el diámetro mide 
?
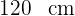De inicio, tenemos que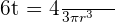 
. Entonces, despejando 
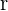y 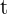tendríamos
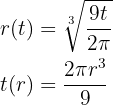
Cuando el diámetro mide 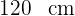, el radio mide 
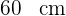o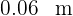 
. Evaluando 
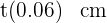obtenemos el tiempo
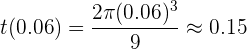
Obteniendo 
y evaluando en 
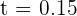tenemos
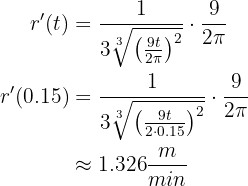
¿Cuál es la velocidad que lleva un vehículo se mueve según la ecuación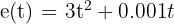 
en el tercer segundo de su recorrido si el espacio se mide en metros y el tiempo en segundos?
La velocidad está dada por la derivada,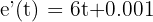 
, entonces para saber la velocidad en el tercer segundo, debemos calcular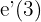 
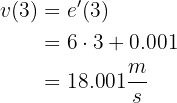
¿Cuál es la velocidad que lleva un vehículo se mueve según la ecuación 
en el quinto segundo de su recorrido? El espacio se mide en metros y el tiempo en segundos.
La velocidad está dada por la derivada, 
, entonces para saber la velocidad en el quinto segundo, debemos calcular 
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La descripcion es erronea donde da la derivada de arcocotangente, ya que dice derivada de arcotangete, se comieron el co, lo que puede llevar a confunciones, como en mi caso que pense que era la derivada de la inversa de tangente, cuando era la derivada de la inversa de cotangente.
Hola entendemos la confusión, pero como sabes en cada lugar toman la notación en forma diferente, en este caso se tomo arccot(x) donde se repite la c para diferenciar de arctan(x).
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Medio tarde me parece mi respuesta, pero simplemente tenes que derivar cada termino independientemente:
7^4=(7.4)^3
e^x-4=e^x-4 (por formula)
lnx=1/x
100=0 (Derivando una constante en terminos de x)
Excelente contenido. Creo es posible mejorar el contenido para que sea más didáctico con más ejemplos, partiendo de lo elemental a lo complejo, para que el texto pueda ser más entendible para estudiantes de secundaria en Costa Rica.
Excelente artículo y muy dinámico.
Agradecemos tu comentario, la verdad estamos trabajando mucho para lograr tener las mejores explicaciones para que sea mas entendible al publico y para ello lo que ustedes recomienden nos ayuda en gran forma, esperamos que en un futuro seamos mejores siguiendo sus sugerencias, otra vez gracias.
Hola: El últipo ejercicio de aplicación me parece que es incorrecto ya que no está obteniendo la derivada del volumen del cono
Hola si te refieres al triángulo que gira, si se derivo el volumen, si estoy equivocado por favor indícamelo.