
El proceso de optimización
Optimizar una función consiste en encontrar sus valores máximos y mínimos, esto significa que hay que encontrar los valores en el dominio de la función para los cuales se alcanza el máximo y mínimo en el codominio . El proceso de optimización hace parte de una de las aplicaciones más importante de la derivada. Para lo cual es útil tener a la mano las derivadas mas comunes y utilizadas. En lo siguiente presentaremos un camino para resolver problemas de optimización y haremos varios ejemplos.
- De las condiciones del problema extraer o plantear la función a maximizar o minimizar.
- En el caso de que en el problema intervengan más de una variable, plantear ecuaciones que relacionen las distintas variables del sistema.
- Despejar una variable de la ecuación y sustituirla en la función de modo que nos quede una función con una sola variable.
- Encontrar los extremos locales, esto significa que debemos igualar la función a cero y resolver la ecuación resultante.
- Realizar la 2ª derivada para comprobar el resultado obtenido.
Ejercicios propuestos
De todos los triángulos isósceles de 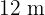 de perímetro, hallar los lados del que tome área máxima.
de perímetro, hallar los lados del que tome área máxima.

La función que tenemos que optimizar o más específicamente maximizar es la función que esta definida por el área del triángulo.
Ya que el triángulo es isósceles, su base es el lado 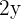 y su altura la podemos calcular usando el teorema de Pitagoras, así obtenemos
y su altura la podemos calcular usando el teorema de Pitagoras, así obtenemos 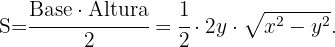
Con la condición de que el perímetro del triángulo mide 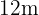 podemos relacionar las variables:
podemos relacionar las variables:

Este resultado lo podemos sustituir en la función:
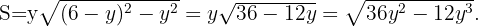
Para hallar los extremos locales, derivamos, igualamos a cero y calculamos las raíces.
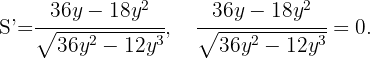
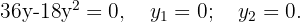
Finalmente con el criterio de la segunda derivada podemos comprobar nuestro resultado.
Recordemos que si la segunda derivada tiene signo negativo, entonces obtendremos un máximo local y si la segunda derivada tiene signo positivo tendremos un mínimo local.
Así realizamos la 2ª derivada y evaluamos en  , ya que la solución
, ya que la solución  la descartamos porque no hay un triángulo cuyo lado sea cero.
la descartamos porque no hay un triángulo cuyo lado sea cero.
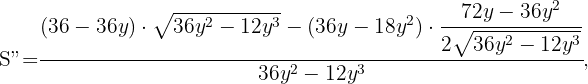
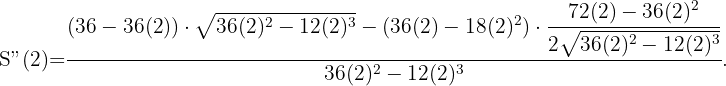
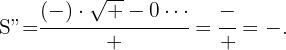
Por lo que queda probado que en  hay un máximo.
hay un máximo.
La base 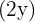 mide
mide  y los lados oblicuos
y los lados oblicuos 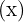 también miden
también miden 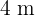 , por lo que el triangulo de área máxima sería un triangulo equilatero.
, por lo que el triangulo de área máxima sería un triangulo equilatero.
Recortando convenientemente en cada esquina de una lámina de cartón de dimensiones  un cuadrado de lado
un cuadrado de lado  y doblando convenientemente (véase figura), se construye una caja. Calcular
y doblando convenientemente (véase figura), se construye una caja. Calcular  para que el volumen de dicha caja sea máximo.
para que el volumen de dicha caja sea máximo.
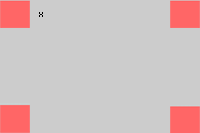
Primero debemos encontrar la función a optimizar. Esta función es definida por el volumen de la caja, la cual tiene como lados a  ,
,  y como altura a
y como altura a  , así nuestra función es
, así nuestra función es
Notemos que en este problema solo interviene una variable, así que podemos pasar directamente a buscar los extremos locales.
Recordemos que para esto debemos derivar nuestra función e igualar la ecuación resultante a cero.
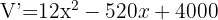
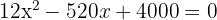
Esta ecuación la podemos resolver utilizando la fórmula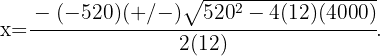
Lo cual nos da las siguientes dos soluciones 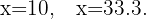
Notemos que la solución 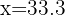 no es validad ya que tendríamos que el lado
no es validad ya que tendríamos que el lado  seria negativo.
seria negativo.
De esta forma nuestro único extremo local es 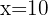 .
.
Calculando la segunda derivada de la función 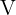 y evaluando en
y evaluando en 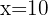 , obtenemos
, obtenemos
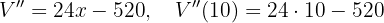
Una hoja de papel debe tener 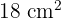 de texto impreso, márgenes superior e inferior de
de texto impreso, márgenes superior e inferior de 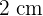 de altura y márgenes laterales de
de altura y márgenes laterales de 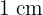 de anchura. Obtener razonadamente las dimensiones que minimizan la superficie del papel.
de anchura. Obtener razonadamente las dimensiones que minimizan la superficie del papel.

La función que debemos minimizar esta dada por el área de la superficie de papel,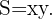
Ahora de las condiciones del problema debemos extraer ecuaciones que relacionen las variable.
De la imagen y ya que debemos tener 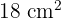 de texto impreso podemos concluir que
de texto impreso podemos concluir que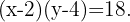
Despejando para  , se sigue que
, se sigue que 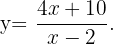
Al remplazar en la función  obtenemos
obtenemos
Ahora podemos derivar la función para encontrar los extremos locales 
Igualamos la derivada a cero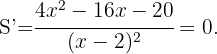
Esto significa que debemos resolver la ecuación 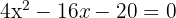 .
.
Notemos que 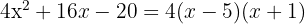
Por tanto nuestras soluciones son  y
y  .
.
Debemos rechazar la solución  pues es negativa.
pues es negativa.
Por lo tanto tenemos una sola solución a nuestro problema. Dado esto no tenemos necesidad de calcular la segunda derivada y podemos concluir que en  y
y 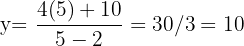 encontramos las dimensiones que minimizan la superficie de papel.
encontramos las dimensiones que minimizan la superficie de papel.
Descomponer el número 44 en dos sumandos tales que el quíntuplo del cuadrado del primero menos el séxtuplo del cuadrado del segundo sea un mínimo.
Primero planteamos la ecuación a solucionar que debemos optimizar.
El primer número lo llamaremos  y el segundo número
y el segundo número  .
.
Ya el quíntuplo del cuadrado del primero menos el séxtuplo del cuadrado del segundo debe ser mínimo entonces nuestra función es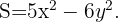
Y relacionamos las dos variables a través de la condición,  se descompone como la suma de dos números, esto es,
se descompone como la suma de dos números, esto es,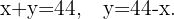
Luego remplazamos el valor de  y obtenemos
y obtenemos 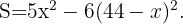
Derivando la función  tenemos
tenemos
Finalmente debemos resolver la siguiente ecuación 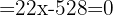 , se consigue la siguiente solución,
, se consigue la siguiente solución,
Y podemos saber el valor  también,
también,  .
.
Así que  es la solución a nuestro problema.
es la solución a nuestro problema.
Al comprobar con el criterio de la segunda derivada se tiene que 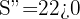 , lo cual nos dice que
, lo cual nos dice que  es un mínimo de la función
es un mínimo de la función  .
.
El valor de un diamante es proporcional al cuadrado de su peso. Divide un diamante de 2 g en dos partes de forma que la suma de los valores de los dos diamantes formados sea mínima.
Digamos que  es el peso de un diamante. Ya que el valor del diamante es proporcional al cuadrado del peso, entonces el valor de nuestro diamante debe estar dado por
es el peso de un diamante. Ya que el valor del diamante es proporcional al cuadrado del peso, entonces el valor de nuestro diamante debe estar dado por  , donde
, donde  es una constante positiva de proporcionalidad.
es una constante positiva de proporcionalidad.
Al dividir un diamante de 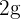 en dos partes de pesos
en dos partes de pesos  y
y  , tenemos una ecuación que nos relaciona, no solo pesos de las partes, si no también sus valores,
, tenemos una ecuación que nos relaciona, no solo pesos de las partes, si no también sus valores,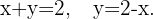
De esta forma los valores de cada una de las partes son,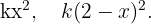
Y la función que deseamos optimizar es la dada por la suma de dichos valores,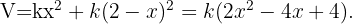
Para encontrar los valores extremos de esta función debemos derivar e igualar a cero,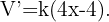

Como podemos ver hemos obtenido una solución  para nuestro problema.
para nuestro problema.
Para comprobar que esta solución nos da un mínimo valor, hallamos la segunda derivada y checamos que es positiva, en efecto,  De esta forma el diamante se ha de dividir en dos partes iguales de 1 g.
De esta forma el diamante se ha de dividir en dos partes iguales de 1 g.
Una boya, formada por dos conos rectos de hierro unidos por sus bases ha de ser construido mediante dos placas circulares de 3 m de radio. Calcular las dimensiones de la boya para que su volumen sea máximo.
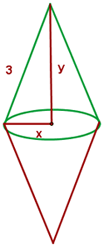
La función que necesitamos maximizar es el doble del volumen de un cono, así
Ya que sus bases estan construidas mediante dos placas circulares de radio  , tenemos que la ecuación que relaciona las variables es
, tenemos que la ecuación que relaciona las variables es
Remplazando en la función 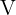 , se sigue que
, se sigue que
Ahora derivamos  e igualamos a cero para hallar los valores extremos
e igualamos a cero para hallar los valores extremos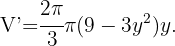
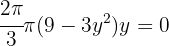
Al solucionar la ecuación anterior obtenemos que,
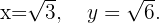
Finalmente debemos evaluar la segunda derivada en 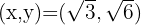 para comprobar que aquí obtenemos un máximo para la función volumen,
para comprobar que aquí obtenemos un máximo para la función volumen,
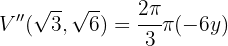 para la función volumen.
para la función volumen.
Se pretende fabricar una lata de conserva cilíndrica (con tapa) de 1 litro de capacidad. ¿Cuáles deben ser sus dimensiones para que se utilice el mínimo posible de metal?
Del enunciado podemos concluir que debemos minimizar la función que define el área de la lata cilíndrica, la cual esta dada por
Ya que lata debe contener un litro entonces su volumen es igual a  , por lo cual
, por lo cual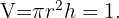
Luego despejando  , se sigue que
, se sigue que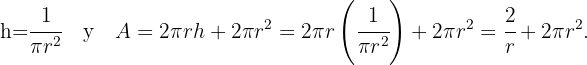 Al deriva la función
Al deriva la función  tenemos que
tenemos que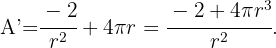
Para hallar los valores extremos igualamos la ecuación anterior a cero y despejamos el valor de 

Luego podemos obtener el valor de  usando el valor de
usando el valor de  , así
, así 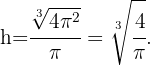
Al comprobar con el criterio de la segunda derivada tenemos que
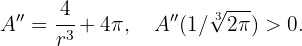
Por lo tanto con 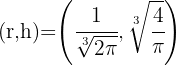 obtenemos que las dimensiones de la lata son mínimas.
obtenemos que las dimensiones de la lata son mínimas.
Se tiene un alambre de 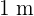 de longitud y se desea dividirlo en dos trozos para formar con uno de ellos un círculo y con el otro un cuadrado. Determinar la longitud que se ha de dar a cada uno de los trozos para que la suma de las áreas del círculo y del cuadrado sea mínima.
de longitud y se desea dividirlo en dos trozos para formar con uno de ellos un círculo y con el otro un cuadrado. Determinar la longitud que se ha de dar a cada uno de los trozos para que la suma de las áreas del círculo y del cuadrado sea mínima.
Si el cuadrado tiene lado  y el círculo tiene radio
y el círculo tiene radio  , entonces la función a optimizar es:
, entonces la función a optimizar es: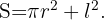
Ya que el alambre tiene una longitud de un  , entonces la suma de los perímetros del círculo y el cuadrado nos da la ecuación que relaciona las variables,
, entonces la suma de los perímetros del círculo y el cuadrado nos da la ecuación que relaciona las variables,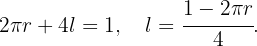
Remplazando en  se sigue,
se sigue,
El siguiente paso es derivar la función  e igualar a cero, para hallar los valor extremos,
e igualar a cero, para hallar los valor extremos,
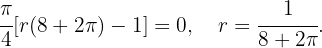
Con este valor para  podemos concluir que Trozo del círculo=
podemos concluir que Trozo del círculo= y Trozo del cuadrado=
y Trozo del cuadrado=
La parte final para este caso de minimizar, como siempre, en este tipo de problemas es encontrar la segunda derivada y checar que es positiva en los valores encontrados 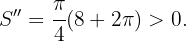
Un sector circular tiene un perímetro de 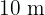 . Calcular El radio y la amplitud del sector de mayor área.
. Calcular El radio y la amplitud del sector de mayor área.
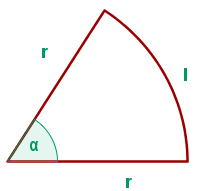
Nuestra función a optimizar es la definida por el área del sector circular, de la figura tenemos: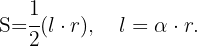
Ya que le perímetro es 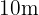 , entonces
, entonces Al remplazar en la función
Al remplazar en la función  , se sigue que
, se sigue que
El siguiente paso es derivar la función  e igualar a cero para encontrar un valor extremo,
e igualar a cero para encontrar un valor extremo,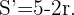
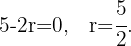
Después de obtener un valor para  podemos obtener valores para
podemos obtener valores para  y
y 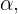

En este caso la segunda derivada de  es constante y negativa,
es constante y negativa,  $$S''=-2<0.$$[/latex] Por lo tanto podemos concluir que los valores antes encontrados nos dan un valor máximo para la función [latex]S[/latex].
$$S''=-2<0.$$[/latex] Por lo tanto podemos concluir que los valores antes encontrados nos dan un valor máximo para la función [latex]S[/latex].
Obtener el triángulo isósceles de área máxima inscrito en un círculo de radio 
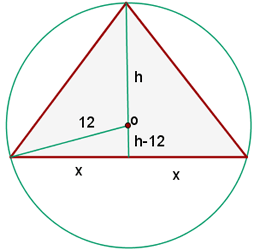
El área del triángulos esta dada por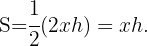
La figura nos muestra un triángulo rectángulo formado usando el radio del círculo, un lado del triángulo y su altura.
Usando el teorema de Pitagoras se sigue que
Al remplazar en  tenemos que
tenemos que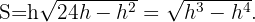
Como siempre el siguen paso es derivar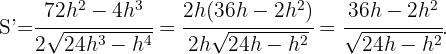
Al igualar a cero concluimos que, 
Con estos valores podemos decir lo siguiente sobre los valores del triángulo,
Base:  ,
,
Lado: 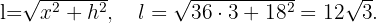
Para concluir o comprobar que estos valores nos dan un máximo para el área debemos evaluar la segunda derivada en 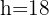 y obtener un valor negativo, en efecto,
y obtener un valor negativo, en efecto, 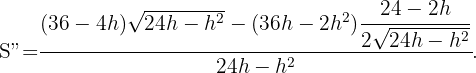
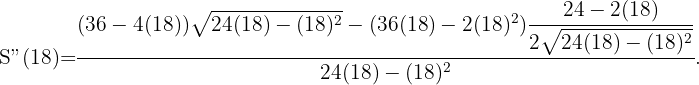
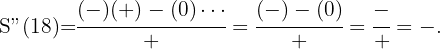
Un triángulo isósceles de perímetro  , gira alrededor de su altura engendrando un cono. ¿Qué valor debe darse a la base para que el volumen del cono sea máximo?
, gira alrededor de su altura engendrando un cono. ¿Qué valor debe darse a la base para que el volumen del cono sea máximo?
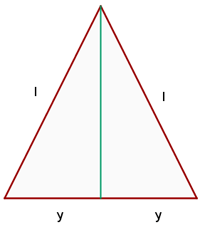
La función a optimizar es definida por el volumen del cono formado al rotar el triángulo,
Ya que el perímetro es  y el triángulo gira alrededor de su altura, de la figura obtenemos lo siguiente
y el triángulo gira alrededor de su altura, de la figura obtenemos lo siguiente
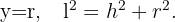
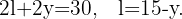
Al combinar estas ecuaciones se sigue que, 
Ya que tenemos todas las variables en términos de  , podemos remplazar en la función volumen,
, podemos remplazar en la función volumen, 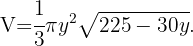
Lo siguiente es derivar, 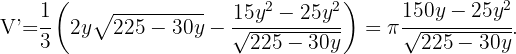
Al igualar a cero obtenemos los siguientes valores para 

y para la base del triángulo,
Base:  ,
,
Para comprobar que en  obtenemos un máximo, debemos evaluar la segunda derivada de
obtenemos un máximo, debemos evaluar la segunda derivada de  es este valor y obtener un valor negativo,
es este valor y obtener un valor negativo,
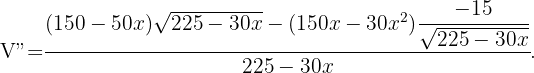
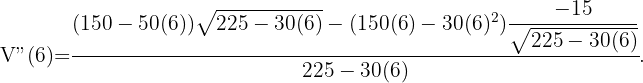














Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
cordial saludo sera que tu me puedes ayudar a resolver un ejercicio que es dada la función f(x)= X elevada a la 2/3 por entre paréntesis (xa la 2 -8) hallar los valores de X para los cuales esta crece te lo agradecería mucho
La descripcion es erronea donde da la derivada de arcocotangente, ya que dice derivada de arcotangete, se comieron el co, lo que puede llevar a confunciones, como en mi caso que pense que era la derivada de la inversa de tangente, cuando era la derivada de la inversa de cotangente.
Hola entendemos la confusión, pero como sabes en cada lugar toman la notación en forma diferente, en este caso se tomo arccot(x) donde se repite la c para diferenciar de arctan(x).
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Medio tarde me parece mi respuesta, pero simplemente tenes que derivar cada termino independientemente:
7^4=(7.4)^3
e^x-4=e^x-4 (por formula)
lnx=1/x
100=0 (Derivando una constante en terminos de x)
Excelente contenido. Creo es posible mejorar el contenido para que sea más didáctico con más ejemplos, partiendo de lo elemental a lo complejo, para que el texto pueda ser más entendible para estudiantes de secundaria en Costa Rica.
Excelente artículo y muy dinámico.
Agradecemos tu comentario, la verdad estamos trabajando mucho para lograr tener las mejores explicaciones para que sea mas entendible al publico y para ello lo que ustedes recomienden nos ayuda en gran forma, esperamos que en un futuro seamos mejores siguiendo sus sugerencias, otra vez gracias.
Hola podrías hacernos el favor de mostrarnos la función para dar una mejor explicación.