Capítulos

Derivadas de funciones trigonométricas
Veremos ejercicios de derivación de funciones trigonométricas, intentaremos escribir el procedimiento lo más detallado posible. Se considerará que ya se conocen las derivadas de las funciones trigonométricas básicas.
Deriva las siguientes funciones

Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, en nuestro ejercicio usaremos  y
y 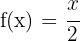 , entonces, nuestra derivada es
, entonces, nuestra derivada es
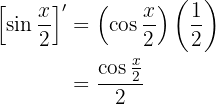

Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
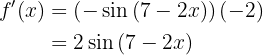
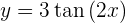
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
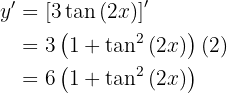

Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
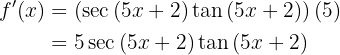

Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Notemos que
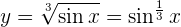
Dicho esto, resolvamos nuestra derivada
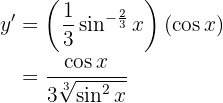
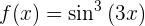
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
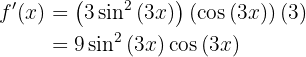
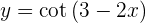
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resultamos nuestra derivada
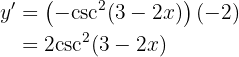
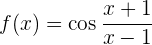
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resultamos nuestra derivada
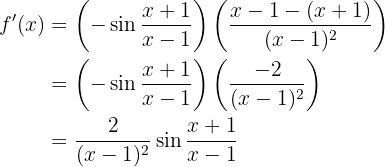
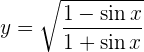
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
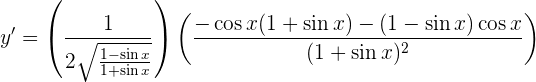
simplificando obtenemos
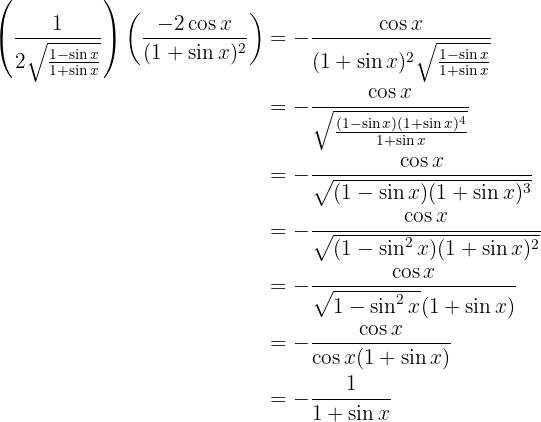
de lo cual se concluye que
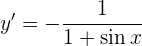
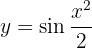
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, en nuestro ejercicio usaremos  y
y 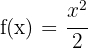 , entonces, nuestra derivada es
, entonces, nuestra derivada es
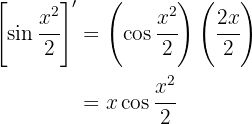
Derivadas de funciones trigonométricas inversas
Deriva las siguientes funciones
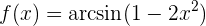
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
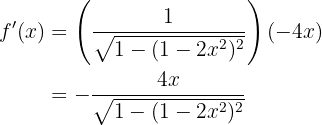
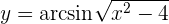
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
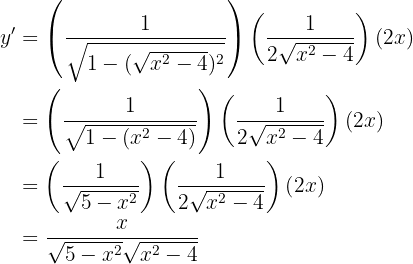
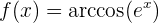
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
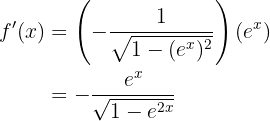
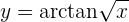
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
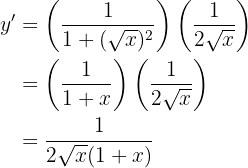
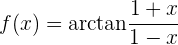
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
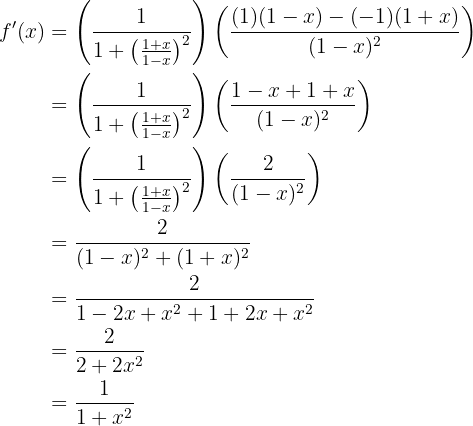
Derivas de funciones compuestas de logaritmos y trigonométricas
Deriva las siguientes funciones
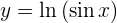
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
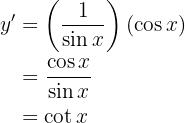

Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
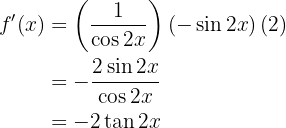
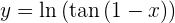
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
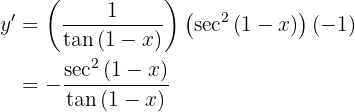
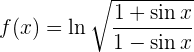
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Antes de derivar, notemos que por propiedades de logaritmo, nuesta función puede ser escrita como

Tomemos

entonces se tiene
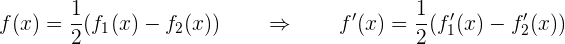
Dicho esto, resolvamos las derivadas. Empecemos con 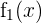
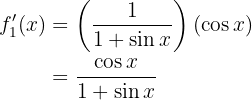
Ahora derivemos 
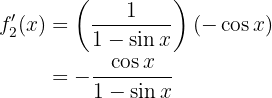
Por lo tanto
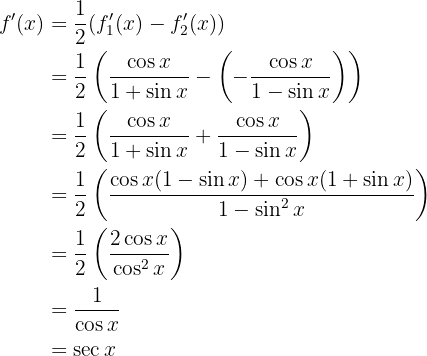

Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada. Primero resolveremos la derivada de la función dentro del argumento del seno, esto es, primero derivaremos

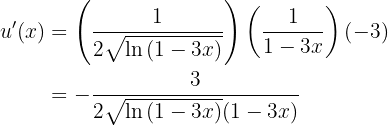
Por lo tanto
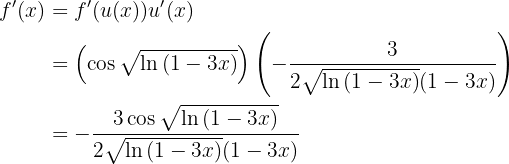
Derivadas de funciones compuestas de exponenciales y trigonométricas
Deriva las siguientes funciones
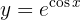
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Ademas de tener en cuenta la regla de la cadena, usaremos derivación implicita, esto para poder encontrar la derivada de  .
.
Dicho esto, resolvamos nuestra derivada
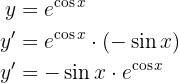
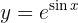
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Ademas de tener en cuenta la regla de la cadena, usaremos derivación implicita, esto para poder encontrar la derivada de  .
.
Dicho esto, resolvamos nuestra derivada
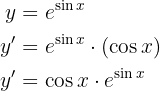
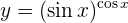
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Ademas de tener en cuenta la regla de la cadena, usaremos derivación implicita, esto para poder encontrar la derivada de  .
.
Dicho esto, resolvamos nuestra derivada
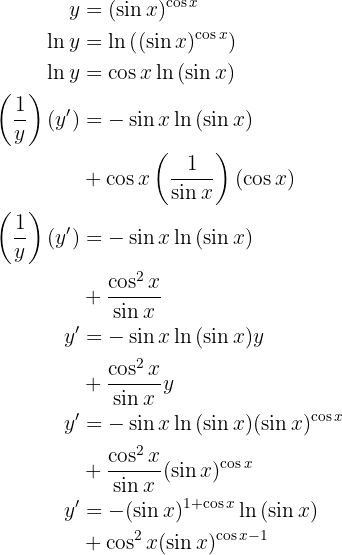
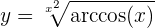
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Ademas de tener en cuenta la regla de la cadena, usaremos derivación implicita, esto para poder encontrar la derivada de  .
.
Dicho esto, resolvamos nuestra derivada
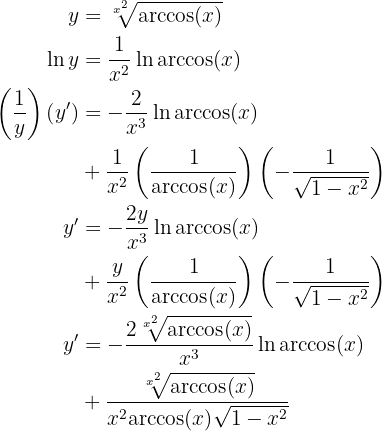
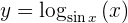
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Primero, dado a las propiedades de logaritmos, podemos hacer cambio de base a logaritmo natural, de donde se sigue que

de donde se sigue que
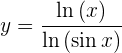
Dicho esto, resolvamos nuestra derivada, usaremos la derivada de cociente de funciones
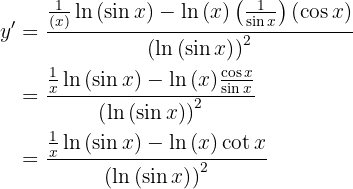
Derivadas sucesivas
Encuentra la formula general de la n-ésima derivada de las siguientes funciones.
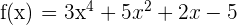
Para obtener la formula primero debemos obtener las primeras derivadas y ver si encontramos algún patrón
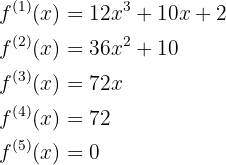
Notemos que la cuarta derivada es una constante,  , por lo tanto, de la quinta derivada en adelante las derivadas serán siempre cero, esto es
, por lo tanto, de la quinta derivada en adelante las derivadas serán siempre cero, esto es

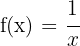
Para obtener la formula primero debemos obtener las primeras derivadas y ver si encontramos algún patrón
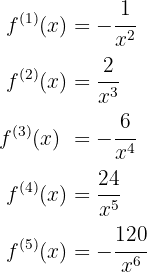
Notemos que en general, la n-ésima derivada está dada por
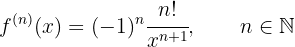

Para obtener la formula primero debemos obtener las primeras derivadas y ver si encontramos algún patrón
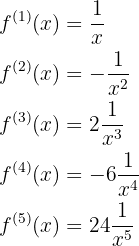
Notemos que, en general, la n-ésima derivada está dada por
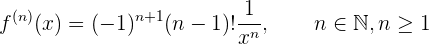
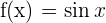
Para obtener la formula primero debemos obtener las primeras derivadas y ver si encontramos algún patrón
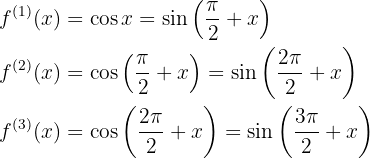
Notemos que con estas primeras derivadas se obtiene que la n-ésima derivada tiene la forma
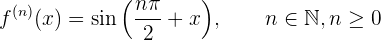

Para obtener la formula primero debemos obtener las primeras derivadas y ver si encontramos algún patrón
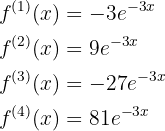
Notemos que la fórmula de la n-ésima derivada está dada por
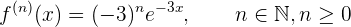
Derivación implícita
En los siguientes ejercicio derivaremos implícitamente. Esta derivación suele ocurrir cuando no podemos despejar a una variable en términos de otra, así que derivamos las variables en términos de la misma variable independiente, esto es, la derivada de  la escribiremos como
la escribiremos como  cada que deba aparecer.
cada que deba aparecer.
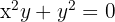
Procedamos derivando implícitamente. Nuestra función es
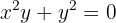
derivando obtenemos
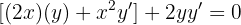
Escribamos la derivada de una forma más conveniente
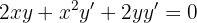
Dejemos los términos con  en el lado izquierdo de la expresión
en el lado izquierdo de la expresión
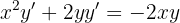
Podemos despejar  del lado izquierdo
del lado izquierdo
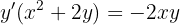
Por lo tanto, nuestra derivada es
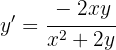
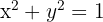
Procedamos derivando implícitamente. Nuestra función es
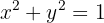
derivando obtenemos
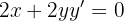
Dejemos los términos con  en el lado izquierdo de la expresión
en el lado izquierdo de la expresión
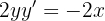
Por lo tanto, nuestra derivada es
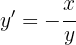
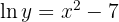
Procedamos derivando implícitamente. Nuestra función es
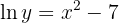
derivando obtenemos
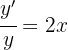
Podemos despejar  del lado izquierdo
del lado izquierdo
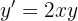
Por lo tanto, nuestra derivada es
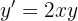

Procedamos derivando implícitamente. Nuestra función es

derivando obtenemos
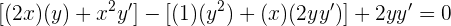
Escribamos la derivada de una forma más conveniente
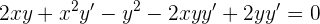
Dejemos los términos con  en el lado izquierdo de la expresión
en el lado izquierdo de la expresión
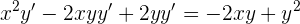
Podemos despejar  del lado izquierdo
del lado izquierdo

Por lo tanto, nuestra derivada es

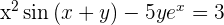
Primero escribiremos nuestra expresión de una forma un poco más conveniente, posteriormente empezaremos a derivar
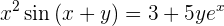
Derivemos

Simplifiquemos

Notemos que podemos factorizar  del lado derecho
del lado derecho
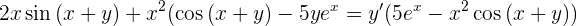
esto nos da como resultado
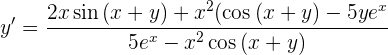
Problemas adicionales de derivación
Deriva las siguientes funciones
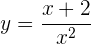
Para obtener esta derivada usaremos la fórmula de derivación de cociente de funciones
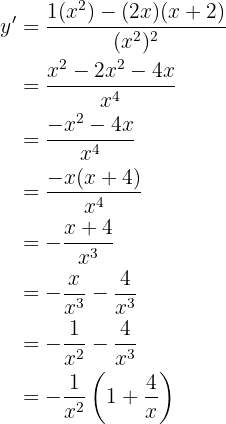
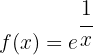
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
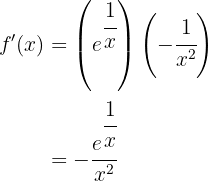
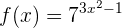
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
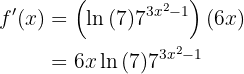

Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Antes de resolver, aplicaremos propiedades de logaritmos para simplificar la expresión a algo más amigable
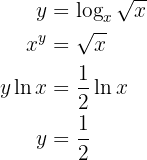
Dicho esto, la derivada de una constante es inmediata
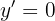
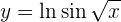
Para obtener la derivada se utiliza la regla de la cadena, en donde, dada la composición de dos funciones

su derivada es

Muchas veces se utiliza  en vez de
en vez de  , es solo notación.
, es solo notación.
Dicho esto, resolvamos nuestra derivada
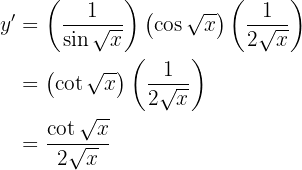













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La descripcion es erronea donde da la derivada de arcocotangente, ya que dice derivada de arcotangete, se comieron el co, lo que puede llevar a confunciones, como en mi caso que pense que era la derivada de la inversa de tangente, cuando era la derivada de la inversa de cotangente.
Hola entendemos la confusión, pero como sabes en cada lugar toman la notación en forma diferente, en este caso se tomo arccot(x) donde se repite la c para diferenciar de arctan(x).
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Medio tarde me parece mi respuesta, pero simplemente tenes que derivar cada termino independientemente:
7^4=(7.4)^3
e^x-4=e^x-4 (por formula)
lnx=1/x
100=0 (Derivando una constante en terminos de x)
Excelente contenido. Creo es posible mejorar el contenido para que sea más didáctico con más ejemplos, partiendo de lo elemental a lo complejo, para que el texto pueda ser más entendible para estudiantes de secundaria en Costa Rica.
Excelente artículo y muy dinámico.
Agradecemos tu comentario, la verdad estamos trabajando mucho para lograr tener las mejores explicaciones para que sea mas entendible al publico y para ello lo que ustedes recomienden nos ayuda en gran forma, esperamos que en un futuro seamos mejores siguiendo sus sugerencias, otra vez gracias.
Hola podrías hacernos el favor de mostrarnos la función para dar una mejor explicación.