Capítulos
Teorema de Bolzano y raíces de una función
Bernhard Placidus Johann Bolzano (1781-1848) fue un matemático checo que trabajo el concepto de continuidad. Uno de sus resultados es el teorema que lleva su nombre.
Teorema de Bolzano. Sea 
una función continua en un intervalo cerrado 
y que toma valores de signo contrario en los extremos, entonces existe al menos un valor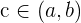 
tal que 
.
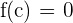En este teorema es de suma importancia que la función sea continua, esto nos permite representar su gráfica como una cuerda que consta de una sola pieza. Si la recta horizontal 
representa el eje 
y los extremos de la cuerda se encuentran en lados opuestos respecto al eje , entonces la cuerda tiene que pasar sobre dicho eje coordenado, esto es, intersecta al eje por lo que es una raíz de la función.
Hay que destacar que el Teorema de Bolzano indica la existencia de un valor 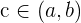, tal que 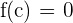, pero no decribe una forma de encontrar este valor.
El Teorema de Bolzano no solamente indica la existencia de una raíz, de hecho puede emplearse para garantizar la existencia de un valor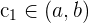 
, tal que 
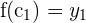, para 
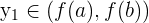. Basta considerar la cuerda antes mencionada y considerar la recta horizontal 
.
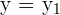Una de las aplicaciones del Teorema de Bolzano es la siguiente: Supongamos que se viaja en automóvil de una ciudad 
hasta una ciudad 
saliendo a las 
y arrivando el mismo día. Si al día siguiente se parte de regreso hacia la ciudad en el mismo horario y tiempo empleado en el viaje de ida, entonces hay un punto en el trayecto en el cual el automóvil se encuentra a la misma hora de ambos días.
Para comprender este problema, sin la necesidad de emplear el teorema de Bolzano, consideramos la trayectoría empleada y colocamos dos automóviles, uno en cada ciudad y que comienzan su recorrido a la misma hora. Entonces resulta sencillo visualizar que en algún punto de camino ambos automóviles se van a encontrar.
Empleando el Teorema de Bolzano consideramos 
la función de distancia recorrida en el viaje de ida a tiempo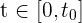 
, esto es 
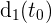es igual a la distancia recorrida de la ciudad a la ciudad . De igual forma 
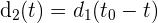es la función de distancia recorrida en el viaje de regreso a tiempo .
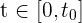Se construye la función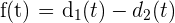 
la cual es continua ya que la función distancia lo es. Notamos que:
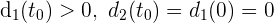
Así, al evaluar la función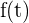 
en los extremos del intervalo 
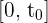se obtiene
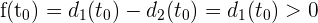
Como los signos en los extremos del intervalo son distintos podemos aplicar el Teorema de Bolzano, luego existe un valor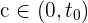 
tal que 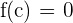, de lo cual se obtiene
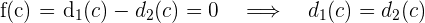
Así, el automóvil se encuentra en el mismo punto a la misma hora en ambos días.
Como podrás notar en este ejemplo no consideramos la forma explícita de la función distancia. A continuación te presentamos una serie de ejemplos donde las funciones a emplear se encuntran en forma explícita
Ejemplos de casos donde aplicamos el teorema de Bolzano
1Comprobar que la ecuación 
tiene al menos una solución real en el intervalo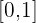 
.
Consideramos la función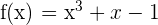 
, que es continua en 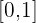por ser polinómica.
Estudiamos el signo en los extremos del intervalo:
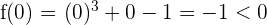
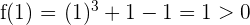
Como los signos son distintos se cumple el teorema de Bolzano, por tanto existe un valor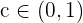 
tal que 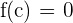. Lo que demuestra que tiene una solución en ese intervalo.
2Comprobar que la ecuación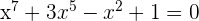 
tiene al menos una solución real en el intervalo 
.
Consideramos la función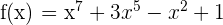 
, que es continua en por ser polinómica.
Estudiamos el signo en los extremos del intervalo:
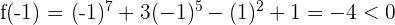
Como los signos son distintos se cumple el teorema de Bolzano, por tanto existe un valor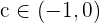 
tal que 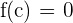. Lo que demuestra que tiene una solución en ese intervalo.
3Comprobar que la ecuación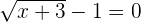 
tiene al menos una solución real en el intervalo 
.
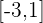Consideramos la función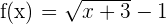 
, que es continua en 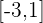ya que es una diferencia de funciones continuas. El dominio es 
.
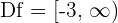Estudiamos el signo en los extremos del intervalo:
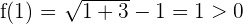
Como los signos son distintos se cumple el teorema de Bolzano, por tanto existe un valor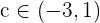 
tal que 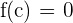. Lo que demuestra que tiene una solución en ese intervalo.
4Comprobar que la ecuación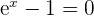 
tiene al menos una solución real en el intervalo 
.
Consideramos la función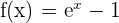 
, que es continua en ya que es una diferencia de funciones continuas en 
.
Estudiamos el signo en los extremos del intervalo:
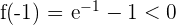
Como los signos son distintos se cumple el teorema de Bolzano, por tanto existe un valor 
tal que 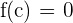. Lo que demuestra que tiene una solución en ese intervalo.
5Comprobar que la ecuación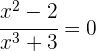 
tiene al menos una solución real en el intervalo 
.
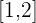Consideramos la función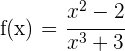 
, que es continua en 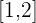ya que es un cociente de polinomios y su dominio es 
.
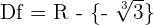Estudiamos el signo en los extremos del intervalo:
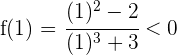
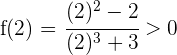
Como los signos son distintos se cumple el teorema de Bolzano, por tanto existe un valor 
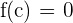tal que . Lo que demuestra que tiene una solución en ese intervalo.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La descripcion es erronea donde da la derivada de arcocotangente, ya que dice derivada de arcotangete, se comieron el co, lo que puede llevar a confunciones, como en mi caso que pense que era la derivada de la inversa de tangente, cuando era la derivada de la inversa de cotangente.
Hola entendemos la confusión, pero como sabes en cada lugar toman la notación en forma diferente, en este caso se tomo arccot(x) donde se repite la c para diferenciar de arctan(x).
me pueden ayudar encontrar la derivada de : y=7 elevado a la 4 + e elevado a la x-4 – ln X + 100
Medio tarde me parece mi respuesta, pero simplemente tenes que derivar cada termino independientemente:
7^4=(7.4)^3
e^x-4=e^x-4 (por formula)
lnx=1/x
100=0 (Derivando una constante en terminos de x)
Excelente contenido. Creo es posible mejorar el contenido para que sea más didáctico con más ejemplos, partiendo de lo elemental a lo complejo, para que el texto pueda ser más entendible para estudiantes de secundaria en Costa Rica.
Excelente artículo y muy dinámico.
Agradecemos tu comentario, la verdad estamos trabajando mucho para lograr tener las mejores explicaciones para que sea mas entendible al publico y para ello lo que ustedes recomienden nos ayuda en gran forma, esperamos que en un futuro seamos mejores siguiendo sus sugerencias, otra vez gracias.
Hola: El últipo ejercicio de aplicación me parece que es incorrecto ya que no está obteniendo la derivada del volumen del cono
Hola si te refieres al triángulo que gira, si se derivo el volumen, si estoy equivocado por favor indícamelo.