Resuelve los siguientes problemas sobre semejanza de triángulos, si tiene dudas, se puede consultar la teoría aquí:
1 Calcular los lados del triángulo semejante
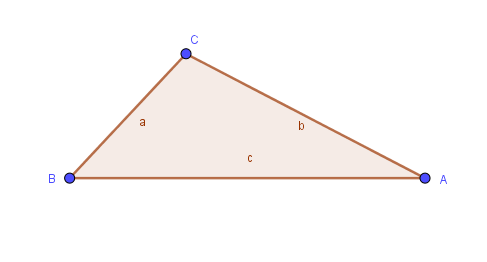
a Sea 
triángulo con lados 
, 
, 
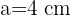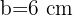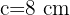y razón de proporcionalidad 
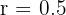, entonces los lados del triángulo semejante son:
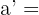
Este campo es obligatorio.
Tenemos que los triángulos son semejantes debido a que sus lados son proporcionales con razón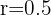 
, entonces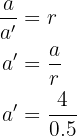
es decir,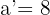 
,.
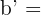
Este campo es obligatorio.
imilarmente,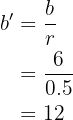
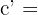
Este campo es obligatorio.
y finalmente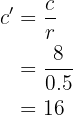
bSea triángulo con lados 
, 
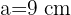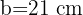y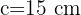 
, entonces considerando una razón 
tendríamos que los lados del triangulo semejante 
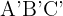son:
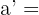
Este campo es obligatorio.
De la misma manera, tenemos que los triángulos son semejantes pero esta vez con , por tanto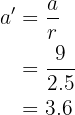
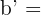
Este campo es obligatorio.
después,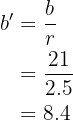
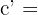
Este campo es obligatorio.
y finalmente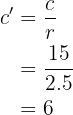
2Los catetos de un triángulo rectángulo miden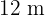 
y 
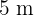. ¿Cuánto medirán los catetos de un triángulo rectángulo cuya hipotenusa mide 
?
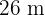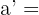
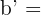
Este campo es obligatorio.
Primeramente calculamos la hipotenusa del primer triángulo rectángulo utilizando Pitágoras y luego calculamos los catetos del segundo a partir de la relación de semejanza.
Hipotenusa del triangulo 1:
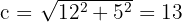de aquí tenemos que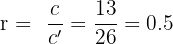 
Con esta razón r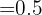
calculamos los catetos del triángulo 2:
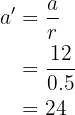y
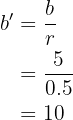
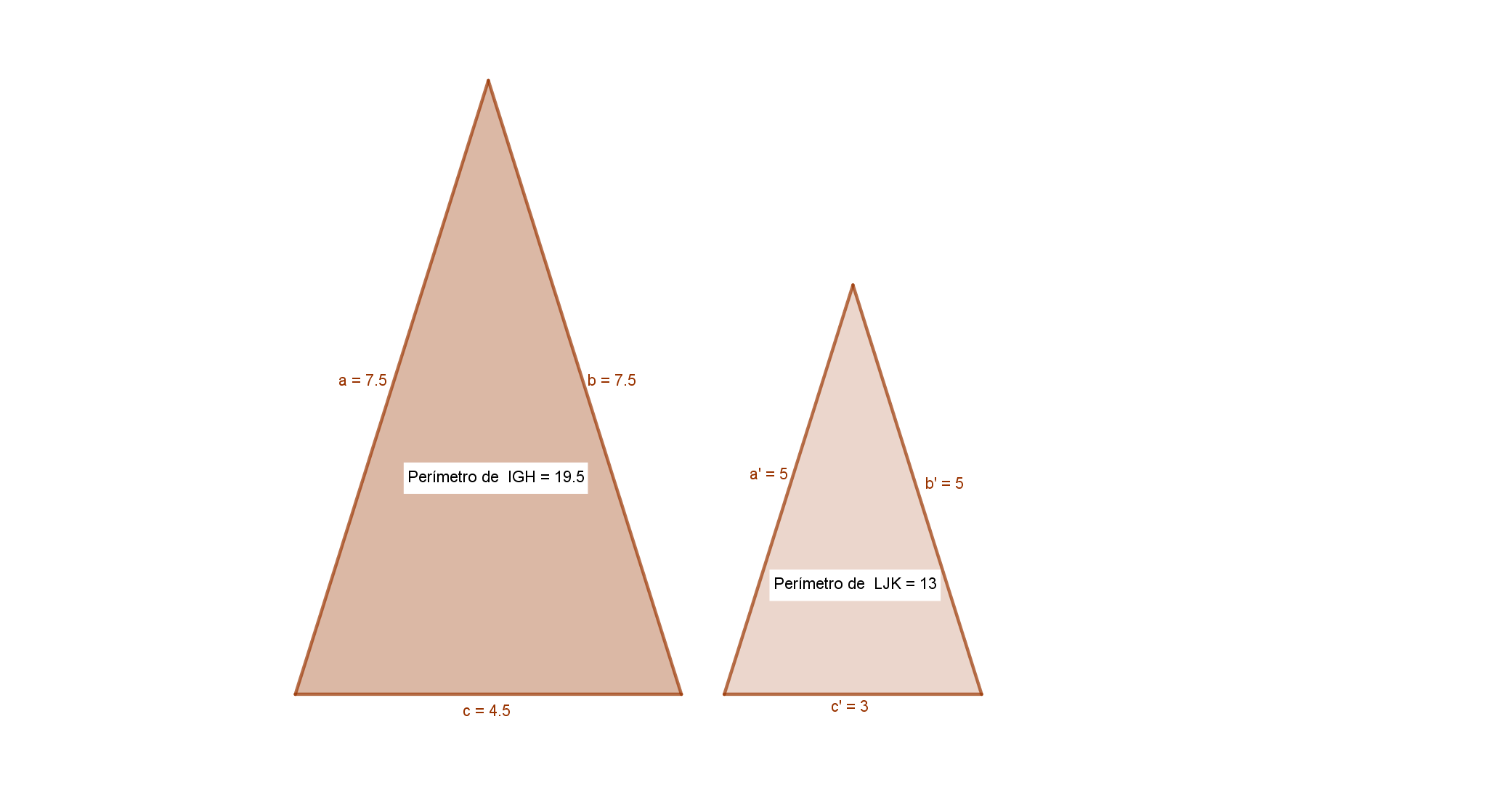
3Sabemos que los perímetros de dos triángulos isósceles semejantes valen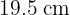 
y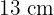 
y que el lado desigual del primero mide 
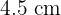. Calcular los lados de ambos triángulos y la razón de semejanza.
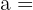
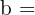
Este campo es obligatorio.
En primer lugar calculamos los lados del triángulo del que conocemos su lado desigual. Como el triángulo es isósceles tiene dos lados iguales, entonces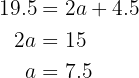
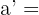
Este campo es obligatorio.
Como los triángulos son semejantes aplicamos la relación de semejanza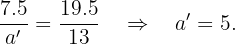
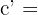
Este campo es obligatorio.
Al ser el triángulo isósceles a' y b' miden lo mismo y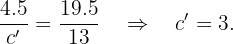
y finalmente,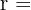 
.
Este campo es obligatorio.
Para la razón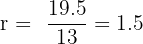
Sabiendo que el área del primer triángulo vale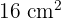 
calcular el área del segundo sin utilizar los lados del mismo
Área: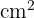 
Este campo es obligatorio.
Para calcular el área utilizamos la razón de semejanza con las áreas (la cual está al cuadrado):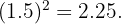
Entonces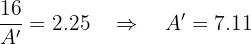 
4 Calcular la altura de un edificio que proyecta una sombra de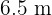 
a la misma hora que un poste de 
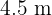de altura da una sombra de 
.
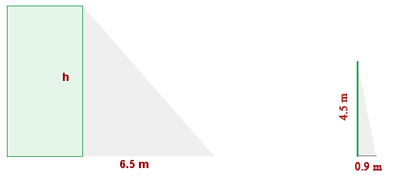
Altura del edificio:
Este campo es obligatorio.
Dado que las sombras son proyectadas a la misma hora, supondremos semejanza para poder dar una solución. Así, dada la semejanza, tenemos la siguiente igualdad
despejando 
obtenemos
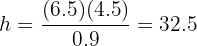
5 ¿Cuál es la razón de proporcionalidad de los siguientes triángulos? 
Razón: 
Este campo es obligatorio.
Podemos tomar cualquier par de lados homólogos, por ejemplo, los lados b y b', y calculamos su razón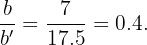
6 En la figura a continuación tendremos que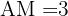 
, 
, 
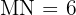y 
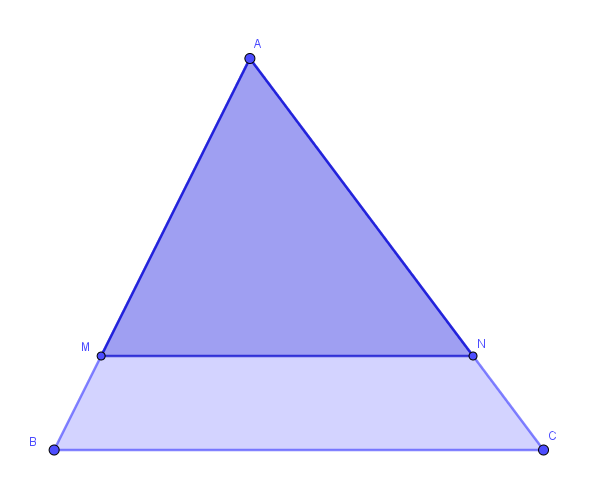
¿Cuánto mide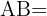 
?
Este campo es obligatorio.
Notemos que para 
tenemos que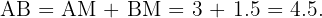
¿Cuánto mide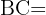 
?
Este campo es obligatorio.
hora bien, puesto que son triángulos semejantes tendremos que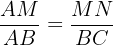
entonces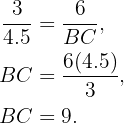
¿Cuánto mide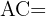 
?
Este campo es obligatorio.
Similarmente,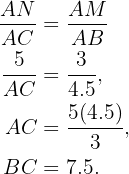
7 Sea triangulo isósceles cuyo lado desigual mide 
y sea 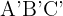triangulo isósceles semejante cuyo lado desigual mide 
y sus otros dos lados (que son iguales) miden 10 
¿Cuánto miden los lados faltantes de ?
Este campo es obligatorio.
Puesto que son triángulos semejantes tendremos que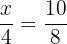
entonces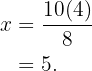
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Buenas, realizo el ejercicio entero pero no me lo corrigen, si no pongo ningún número me poner como mal y si pongo las soluciones bien, directamente es que no me sale ni el cuadrito en verde ni mi puntuación final.
Hola una disculpa, estamos realizando cambios en la plataforma para corregir este tipo de errores.
En los ejercicios debeis poner más numeros y menos letras porque hay algunos ejercicios que es todo letras y no hai ni un número,debeis corregir eso pero el resto todo genial,Gracias
Hola entendemos tu confusión con este tipo de ejercicios, pero tenemos que ser diversos en cuanto al conocimiento ya que este tipo de ejercicios los necesitan estudiantes que profundizan en los temas, es por lo cual que ponemos ejercicios con números y ejercicios teóricos (con muchas letras), te gradecemos tu aportación.
todas me quedaron bien pero me califican 9.0
Hola que bueno que practicas en nuestra pagina, en cuanto el error que mencionas estamos restaurando la pagina para evitar estas situaciones por lo que te pedimos un poco de paciencia.