Determinar el lado de un triángulo equilátero cuyo perímetro es igual al de un cuadrado de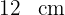 
de lado. ¿Serán iguales sus áreas?
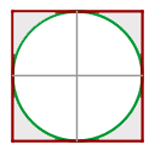
1Representamos gráficamente el cuadrado
2Su perímetro es 
. Para calcular el área empleamos
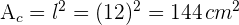
3El triángulo equilátero tiene sus tres lados iguales, por lo que si su perímetro es de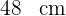 
, entonces cada uno de sus lados mide 
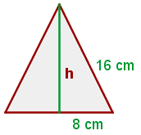
4Para encontrar el área requerimos conocer su altura, para esto dividimos el triángulo equilátero en dos triángulos rectángulos y aplicamos el teorema de Pitágoras
5Para calcular su área, empleamos
Así, ambas figuras tienen el mismo perímetro, pero distinta área.
Calcular el área de un triángulo equilátero inscrito en una circunferencia de radio 
1Representamos gráficamente el problema
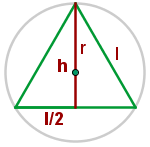
2El centro de la circunferencia es el baricentro, por tanto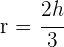 
y se obtiene
3Para encontrar el área del triángulo requerimos conocer su base, para esto dividimos el triángulo equilátero en dos triángulos rectángulos y aplicamos el teorema de Pitágoras
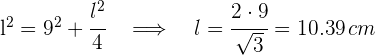
4Para calcular su área, empleamos
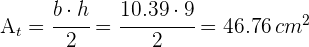
Dado un triángulo equilátero de 
de lado, hallar el área de uno de los sectores determinado por la circunferencia circunscrita y por los radios que pasan por los vértices
1Representamos gráficamente el problema
2El centro de la circunferencia es el baricentro, por tanto 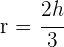y se obtiene
3Para encontrar el radio, necesitamos conocer la altura, para esto dividimos el triángulo equilátero en dos triángulos rectángulos y aplicamos el teorema de Pitágoras
4Calculamos el radio
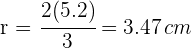
5Así, el área solicitada es
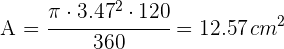
Determinar el área del cuadrado inscrito en una circunferencia de longitud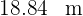 
1Representamos gráficamente el problema
2Necesitamos conocer un lado del cuadrado, para esto primero calculamos el radio a partir de conocer la circunferencia
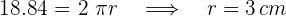
3Para encontrar el lado del cuadrado, consideramos el triángulo rectángulo isósceles cuyos lados iguales son los radios de la circunferencia
4Así, el área del cuadrado es
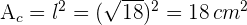
En un cuadrado de 
de lado se inscribe un círculo y en este círculo un cuadrado y en este otro círculo. Hallar el área comprendida entre el último cuadrado y el último círculo
1Representamos gráficamente el problema
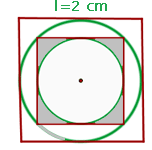
2Necesitamos conocer los radios de los círculos; para esto observamos que el lado del cuadrado de lado es igual al diámetro del círculo inscrito
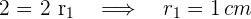
3El díámetro del primer círculo es igual a la diagonal del segundo cuadrado, aplicando e teorema de Pitágoras obtenemos el lado del segundo cuadrado
4Así, el área del segundo cuadrado es
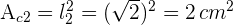
5El diámetro del segundo círculo es igual al lado del segundo cuadrado
6El área el segundo círculo es
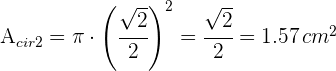
7Así, el área solicitada es
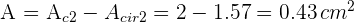
Calcular el área de la corona circular determinada por las circunferencias inscrita y circunscrita a un cuadrado de 
de diagonal
1Representamos gráficamente el problema
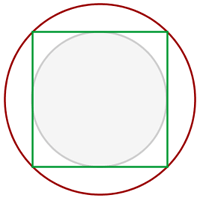
2Necesitamos conocer los radios de los círculos; para esto observamos que el diámetro de la circunferencia circunscrita es igual a la diagonal del cuadrado
3El díámetro de la circunferencia inscrita es igual al lado del cuadrado, aplicando e teorema de Pitágoras obtenemos
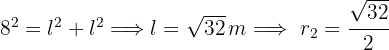
4El área de la corona circular es
En una circunferencia de radio igual a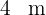 
se inscribe un cuadrado y sobre los lados de este y hacia el exterior se construyen triángulos equiláteros. Hallar el área de la estrella así formada
1Representamos gráficamente el problema
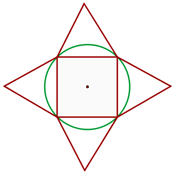
2Necesitamos conocer el lado del cuadrado; para esto observamos que el diámetro de la circunferencia es igual a la diagonal del cuadrado. aplicando el teorema de Pitágoras se obtiene
3El área del cuadrado es
4Para encontrar el área del triángulo equilátero, dividimos en dos triángulos rectángulos y aplicamos el teorema de Pitágoras para encontrar la altura
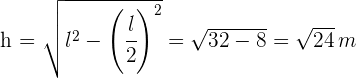
5El área del triángulo es
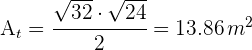
6El área de la estrella es
El perímetro de un trapecio isósceles es de 
, las bases miden 
y 
respectivamente. Calcular los lados no paralelos y el área
1Representamos gráficamente el problema
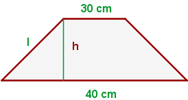
2 Como las bases suman 
, entonces los lados suman 
, luego cada lado mide 
. Para conocer la altura construimos un triángulo rectángulo como en la figura. empleando el teorema de Pitágorasse tiene
3Calculamos el área del trapecio
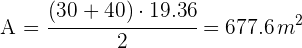
Si los lados no paralelos de un trapecio isósceles se prolongan, quedaría formado un triángulo equilátero de de lado. Sabiendo que el trapecio tiene la mitad de la altura del triángulo, calcular el área del trapecio
1Representamos gráficamente el problema
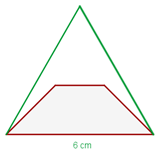
2 Para conocer la altura del triángulo, construimos un triángulo rectángulo cuya base es la mitad de su altura. Empleando el teorema de Pitágoras se tiene
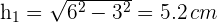
3Calculamos la altura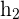 
del trapecio
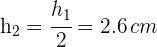
4Calculamos el área del trapecio
El área de un cuadrado es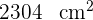 
. Calcular el área del hexágono regular que tiene su mismo perímetro
1Representamos gráficamente el problema
2 Para conocer el perímetro del cuadrado, debemos calcular el valor de uno de sus lados
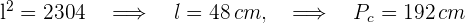
3Calculamos la apotema del hexágono, para ello requerimos el lado del hexágono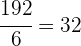 
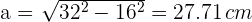
4Calculamos el área del hexágono
La superficie de una mesa está formada por una parte central cuadrada de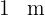 
de lado y dos semicírculos adosados en dos lados opuestos. Calcula el área
1Representamos gráficamente el problema
2 Para conocer el área de la mesa, necesitamos encontrar el área del cuadrado y del círculo
3Calculamos el área del cuadrado
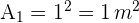
4Calculamos el área del círculo de radio 
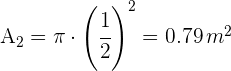
5El área de la mesa es
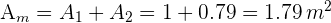
Hallar el área de un sector circular cuya cuerda es el lado del triángulo equilátero inscrito, siendo el radio de la circunferencia
1Representamos gráficamente el problema
2 Para conocer el área del sector señalado en verde, basta observar que el círculo se divide en tres sectores iguales de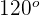 
3Calculamos el área del círculo
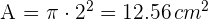
4Calculamos el área del sector círcular
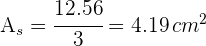
Hallar el área del sector circular cuya cuerda es el lado del cuadrado inscrito, siendo 
el radio de la circunferencia
1Representamos gráficamente el problema
2 Para conocer el área del sector señalado en verde, basta observar que el círculo se divide en cuatro sectores iguales de 
3Calculamos el área del círculo
4Calculamos el área del sector círcular
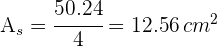
Dadas dos circunferencias concéntricas de radio 
y 
respectivamente, se trazan los radios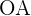 
y 
, que forman un ángulo de 
. Calcular el área del trapecio circular formado
1Representamos gráficamente el problema
2 Para conocer el área del sector señalado en verde, basta observar que el círculo se divide en seis sectores iguales de
3Calculamos el área de cada círculo
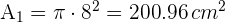
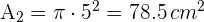
4Calculamos el área de cada sector
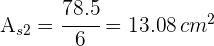
5Calculamos el área del trapecio circular
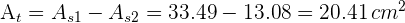
y el radio del círculo mide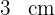 
1Calculamos el área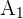 
del cuadrado
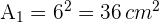
2 Calculamos el área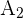 
del círculo
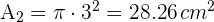
3Calculamos el área sombreada
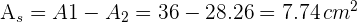
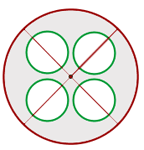
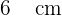y el radio de los círculos pequeños miden
1Calculamos el área 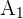del círculo mayor
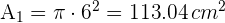
2 Calculamos el área 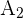del círculo pequeño
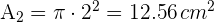
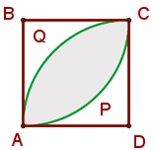
3Calculamos el área sombreada
, 
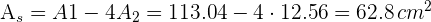
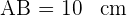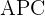un cuadrado y 
y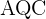 
arcos de circunferencia de centros 
y 
1La parte sombreada se compone de dos segmentos circulares:
2 Calculamos el área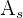 
del sector
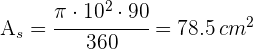
3Calculamos el área del triangulo
4Calculamos el área del segmento circular
5El área sombreada es
A un hexágono regular de lado se le inscribe una circunferencia y se le circunscribe otra. Hallar el área de la corona circular así formada
1Representamos gráficamente
2 Calculamos el radio de la circunferencia circunscrita, para esto observamos que el hexágono se divide en seis triángulos equiláteros iguales, por lo que
3Calculamos el radio de la circunferencia inscrita, este coincide con la altura del triángulo equilátero
4Calculamos el área de la corona circular, la cual se obtiene a partir de la diferencia de áreas de los círculos
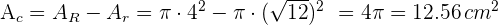
En una circunferencia una cuerda de 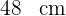y dista 
del centro. Calcular el área del círculo
1Representamos gráficamente
2 Consideramos el triángulo rectángulo como se muestra en la figura y empleando el teorema de Pitágoras, calculamos el radio
3Calculamos el área del círculo
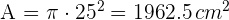
Los catetos de un triángulo rectángulo inscrito en una circunferencia miden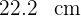 
y 
respectivamente. Calcular el área del círculo
1Representamos gráficamente
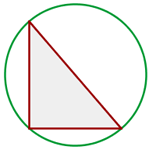
2 La hipotenusa concide con el diámetro del círculo. Empleando el teorema de Pitágoras, calculamos el radio
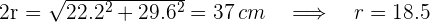
3Calculamos el área del círculo
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
8 Un rectángulo tiene un ancho de 3 unidades. El largo del rectángulo es 5 veces su ancho. ¿Cuál es el área del rectángulo?
45u²
unidades
El largo es
Ahora bien, su área es
hola
No,entiendo si estoy poniendo bien el resultado por que me dice que esta mal ? si,estoy poniendo el resultado que aparece en la solución ya lo corregi 5 veces esta mal copiado ? por favor me dicen cual es el problema
Hola tienes razón, tu resultado es correcto, pero en este momento estamos remodelando la pagina y corriendo errores así que pronto vamos a corregir este que mencionas.
Todo bien con los otros ejercicios pero no me fue posible realizar el 1 y 2
Hola estamos a tu disposición para cualquier duda, solo menciona de manera especifica donde te atoras y con gusto te ayudamos.
Hola, soy Clarisa Israel, Ingeniera en Construcciones. Entiendo que el Romboide es un cuadrilátero con caracteristicas especiales y su nombre indica que tiene un parecido con el Rombo. Ese parecido tiene que ver con que sus diagonales son perpendiculares, y se cortan en el punto medio de una de ellas pero no de la otra. De esa manera al unir los puntos, 2 de sus lados consecutivos resultan de igual longitud y los 2 restantes también tienen igual longitud pero distinta a la de los primeros. NO es un paralelogramo pues sus lados opuestos no son paralelos. Tiene la típica forma de un Barrilete.
El material del sitio me parece muy interesante!!
Espero consideren este comentario.
Atentamente
Hola muchas gracias por tu aportación, lo tomaremos en cuenta para mejorar en nuestro contenido.
Se cumple que BM = MC y AQ = QM con A – Q – M y B – M − C. Si a(ABQ) = 8 ul^2, determine el área del ∆ABC.
No me deja poner 45u²
Hola puedes hacernos el favor de decirnos el número de ejercicio para poder corregirlo.