Resuelve los siguientes problemas:
La hipotenusa de un triángulo rectángulo mide 
cm y uno de sus catetos mide 
cm. ¿Cuál es la medida del otro cateto?
cm
Este campo es obligatorio.
Aplicamos el teorema de Pitágoras:
Tenemos dos triángulos. Un triángulo 
cuyas medidas son 
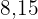y 
y otro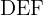 
de medidas 
y 
. Escribe sí o no para indicar si los triángulos son o no rectángulos.
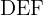
Este campo es obligatorio.
En ambos casos probaremos si se cumple o no el teorema de Pitágoras y para ello deberemos tener en cuenta que la hipotenusa, que en caso de existir, siempre es el lado mayor.
1 Realizamos el cálculo para el triángulo .
Se cumple el teorema de Pitágoras, por el que el triángulo si es rectángulo.
2 Realizamos el cálculo para el triángulo .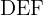
No se cumple el teorema de Pitágoras, por el que el triángulo 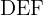no es rectángulo.
Una escalera de 
m de altura se apoya con el pie a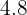 
m de la pared para arreglar un problema que hay en la azotea de una casa. ¿A qué altura se encuentra la azotea?
Este campo es obligatorio.
Aplicamos el teorema de Pitágoras para la altura 
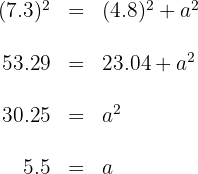
Entonces, la azotea se encuentra 
m.
Las medidas de los catetos de un triángulo rectángulo son 
y 
cm respectivamente. ¿Cuál es la medida de la hipotenusa? Redondea a dos cifras decimales.
h = cm.
Este campo es obligatorio.
Aplicamos el teorema de Pitágoras para obtener la hipotenusa 
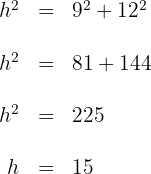
La medida de la hipotenusa es 
cm.
Calcula las proyecciones 
y 
, de los catetos sobre la hipotenusa, usando el teorema del cateto y el de la altura respectivamente.Redondea a dos cifras decimales caso de ser necesario.
n = cm.
m = cm.
Este campo es obligatorio.
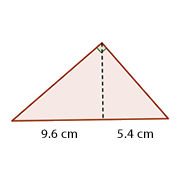
Aplicamos el teorema del cateto para obtener las medidas de las proyecciones de los mismos.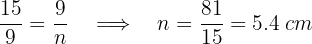 
La proyección del cateto 
mide 
cm.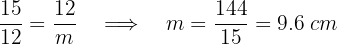 
La proyección del cateto 
mide 
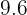cm.
Para instalar una antena parabólica se utiliza un poste sujeto por dos cables como indica la figura.
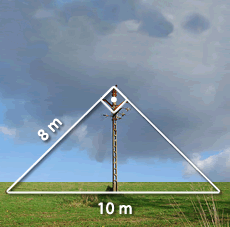
Indica la medida del cable que falta m.
¿A qué distancia del poste habrá que colocar dicho cable? m.
Este campo es obligatorio.
1 Como los dos cables forman un triángulo rectángulo calculamos la medida del cable que falta por Pitágoras.
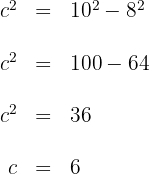
La medida del cable es 6 m.
2 Para calcular la distancia a la que debemos colocar el cable aplicamos el teorema del cateto.
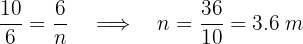
Debemos colocar el cable a 
m del poste.
¿Cuál es la altura del poste? m.
Este campo es obligatorio.
Para calcular la altura del poste aplicamos Pitágoras al triángulo rectángulo que aparece en la figura cuya hipotenusa es 
m y cuya base mide m.
La altura del poste es 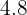m.
Si tienes dudas puedes consultar la teoría
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.