Capítulos
- Teorema de Pitágoras
- Teorema del cateto
- Teorema de la altura
- Diagonal del cuadrado
- Diagonal del rectángulo
- Lado oblicuo del trapecio rectángulo
- Altura del trapecio isósceles
- Altura del triángulo equilátero
- Apotema de un polígono regular
- Lado de un triángulo equilátero inscrito
- Lado de un cuadrado inscrito
A continuación veremos varias fórmulas relacionadas con triángulos rectángulos, muchas de estas se derivan del conocido teorema de Pitágoras por lo que este será el primero que mencionaremos.
Teorema de Pitágoras
"En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos."
Del enunciado anterior tenemos la siguiente fórmula
de la cual podemos calcular la magnitud de cada una de los lados de un triángulo rectángulo
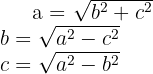
Teorema del cateto
"En un triángulo rectángulo, el cuadrado de uno de los catetos es igual al producto de su proyección sobre la hipotenusa por la propia hipotenusa."
Representamos el enunciado anterior con las siguientes ecuaciones
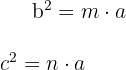
Teorema de la altura
"En un triángulo rectángulo, el cuadrado de la altura medida sobre la hipotenusa es igual al producto de las proyecciones de los dos catetos sobre la hipotenusa."
Del enunciado anterior se desprende la siguiente fórmula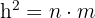
Diagonal del cuadrado
Notemos que la diagonal del cuadrado es la hipotenusa de un triángulo rectángulo con dos catetos iguales,
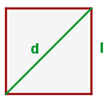
entonces la ecuación de su diagonal es
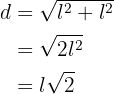
Diagonal del rectángulo
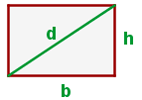
Similarmente al caso anterior, notemos que la diagonal del rectángulo es la hipotenusa de un triángulo rectángulo cuyos catetos son los lados del rectángulo
entonces la ecuación de su diagonal es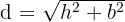
Lado oblicuo del trapecio rectángulo
Notemos que en un trapecio rectángulo, uno de los lados forma un triángulo rectángulo
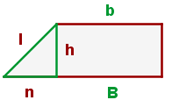
donde la hipotenusa es el lado oblicuo, un cateto es la altura y el otro, la diferencia entre las bases. Por lo tanto, su lado oblicuo se calcula utilizando el teorema de Pitágoras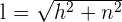
donde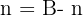
Altura del trapecio isósceles
Para obtener la altura de un trapecio isósceles, utilizamos un triángulo rectángulo donde la hipotenusa es el lado oblicuo, un cateto es la altura y el otro cateto es la diferencia entre 
y 
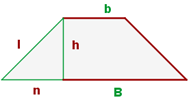
entonces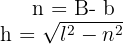 
Altura del triángulo equilátero
Observemos que la altura en un triángulo equilátero también se puede calcular a partir del teorema de Pitágoras
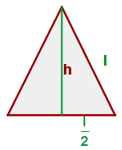
los lados 
,
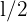son los catetos y 
la hipotenusa, por tanto
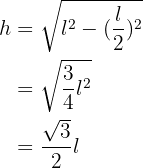
Apotema de un polígono regular
Notemos que podemos calcular el apotema de un polígono regular, conociendo su lado y su radio
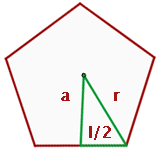
aplicando el teorema de Pitágoras tendremos que la formula del apotema es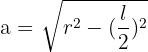
Lado de un triángulo equilátero inscrito
Para calcular el lado del triangulo inscrito, construyamos un pequeño triangulo equilátero adicional como en la figura
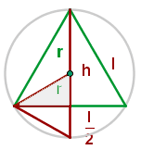
de aquí, notemos que
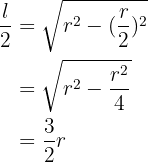
entonces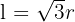
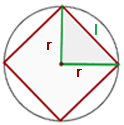
Lado de un cuadrado inscrito
Observemos que
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
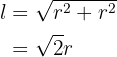
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
8 Un rectángulo tiene un ancho de 3 unidades. El largo del rectángulo es 5 veces su ancho. ¿Cuál es el área del rectángulo?
45u²
unidades
El largo es
Ahora bien, su área es
hola
No,entiendo si estoy poniendo bien el resultado por que me dice que esta mal ? si,estoy poniendo el resultado que aparece en la solución ya lo corregi 5 veces esta mal copiado ? por favor me dicen cual es el problema
Hola tienes razón, tu resultado es correcto, pero en este momento estamos remodelando la pagina y corriendo errores así que pronto vamos a corregir este que mencionas.
Todo bien con los otros ejercicios pero no me fue posible realizar el 1 y 2
Hola estamos a tu disposición para cualquier duda, solo menciona de manera especifica donde te atoras y con gusto te ayudamos.
Hola, soy Clarisa Israel, Ingeniera en Construcciones. Entiendo que el Romboide es un cuadrilátero con caracteristicas especiales y su nombre indica que tiene un parecido con el Rombo. Ese parecido tiene que ver con que sus diagonales son perpendiculares, y se cortan en el punto medio de una de ellas pero no de la otra. De esa manera al unir los puntos, 2 de sus lados consecutivos resultan de igual longitud y los 2 restantes también tienen igual longitud pero distinta a la de los primeros. NO es un paralelogramo pues sus lados opuestos no son paralelos. Tiene la típica forma de un Barrilete.
El material del sitio me parece muy interesante!!
Espero consideren este comentario.
Atentamente
Hola muchas gracias por tu aportación, lo tomaremos en cuenta para mejorar en nuestro contenido.
Se cumple que BM = MC y AQ = QM con A – Q – M y B – M − C. Si a(ABQ) = 8 ul^2, determine el área del ∆ABC.
No me deja poner 45u²
Hola puedes hacernos el favor de decirnos el número de ejercicio para poder corregirlo.