En lo siguiente presentamos dos usos del Teorema de Pitágoras. Calcularemos el valor de las diagonales de un cuadrado y un rectángulo. Recordemos que el Teorema de Pitágoras establece lo siguiente: Dado un triángulo rectángulo de lados  ,
,  e hipotenusa
e hipotenusa  , se satisface
, se satisface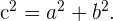
1 Diagonal del cuadrado
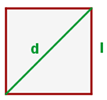
Sea  la diagonal del cuadrado y
la diagonal del cuadrado y  el valor de uno de sus lados. Notemos que al trazar la diagonal del cuadrado, esta nos divide el cuadrado en dos triángulos rectángulos de lados
el valor de uno de sus lados. Notemos que al trazar la diagonal del cuadrado, esta nos divide el cuadrado en dos triángulos rectángulos de lados  e hipotenusa
e hipotenusa  . Para calcular el valor de
. Para calcular el valor de  utilizamos el Teorema de Pitagoras,
utilizamos el Teorema de Pitagoras,
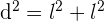

Ejemplo:
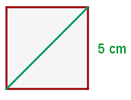
En este cuadrado tenemos que el valor del lado  es
es  , entonces por la fórmula anterior el valor de su diagonal es
, entonces por la fórmula anterior el valor de su diagonal es

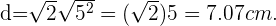
2 Diagonal del rectángulo
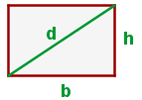
Sea  la diagonal de un rectángulo de lados
la diagonal de un rectángulo de lados  y
y  . Notemos que al trazar la diagonal del rectángulo, esta nos divide el rectángulo en dos triángulos rectángulos de lados
. Notemos que al trazar la diagonal del rectángulo, esta nos divide el rectángulo en dos triángulos rectángulos de lados  ,
,  e hipotenusa
e hipotenusa  . Para calcular el valor de
. Para calcular el valor de  utilizamos el Teorema de Pitagoras,
utilizamos el Teorema de Pitagoras,
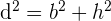
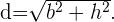
Ejemplo:
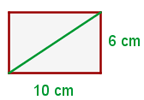
Este rectángulo tiene como lados 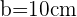 y
y  , entonces por la fórmula anterior el valor de su diagonal es
, entonces por la fórmula anterior el valor de su diagonal es
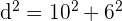
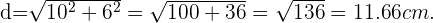
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.