Resuelve los siguientes problemas:
Indica el área de un círculo de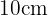 
de diámetro, redondeando a dos cifras decimales.
cm²
¿Cuál sería la longitud de la circunferencia correspondiente? Redondea también a dos cifras decimales.
cm
Este campo es obligatorio.
Como el diámetro es 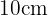el radio es igual a la mitad que es 
. Usando la fórmula para el área de un circulo tenemos que 
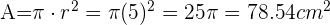Ahora la longitud de la circunferencia esta dada por la formula 
Para nuestro caso tenemos que 
El área del círculo es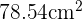 
y la longitud de la circunferencia es 
.
En una imprenta hacen pegatinas para discos de música de forma que se cubra la parte superior del CD. Sabiendo que el radio mayor mide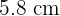 
y el menor 
aproximadamente, ¿qué área de papel utilizan para cada CD?
cm²
Este campo es obligatorio.
Cada CD tiene un circulo mayor y circulo menor. El área del CD no es mas que la resta del área del circulo mayor menos el área del circulo menor. Si el circulo mayor tiene radio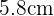 
, entonces su área es 
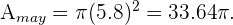Si el circulo menor tiene radio 
, entonces su área es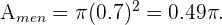 
Por lo tanto el área de cada CD es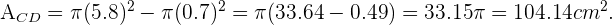 
Dado que el área del CD corresponde al área de papel utilizado podemos concluir el área de cada pegatina es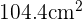 
.
Calcula el área de un sector circular de angulo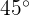 
sabiendo que la longitud de la circunferencia a la que pertenece mide 
.
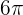cm²
Este campo es obligatorio.
Sabemos que la longitud de la circunferencia esta dada por 
; con esto podemos calcular el radio de la circunferencia de la siguiente forma,
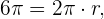
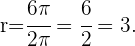
Ahora utilizando el área del sector circular,
Podemos calcular el área de sector circular de ángulo ,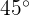
Para una fiesta de cumpleaños un grupo de 
amigos compran una tarta de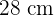 
de diámetro. Si dividimos el pastel en porciones iguales, ¿qué área de tarta se come cada uno?
cm²
Este campo es obligatorio.
El área de cada trozo corresponde al área de sector circular. Para calcular esta área debemos hallar primero el radio de la tarta. Dado que la tarta tiene diámetro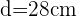 
, entonces su radio es la mitad 
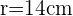. Ahora hallaremos el ángulo de cada trozo. Dado que la tarta de se divide en iguales tenemos que el ángulo es
Finalmente utilizamos el área del sector circular,
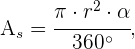
que en nuestro caso se convierte en
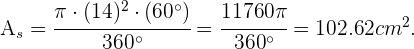
De esto concluimos que cada trozo tiene área 
.
Sobre un círculo de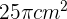 
de área trazamos un ángulo central de 
. Calcula el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente
cm²
Este campo es obligatorio.
Dado que el área del circulo es 
podemos hallar el radio del circulo de la siguiente forma,
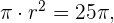
Sabemos que el ángulo central que determina el trozo es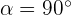 
. Con esta información podemos determinar el área del sector circular
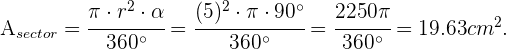
Para hallar el área deseada debemos primero hallar el área del triángulo isósceles formado por los radio del circulo, la cual es
Ahora al restar el área del segmento circular menos el área del triángulo hallamos el área buscada
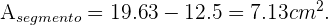
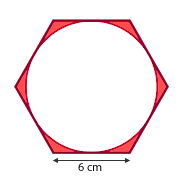
Calcular el área de la zona coloreada de las siguientes figuras siendo la altura del rectángulo la mitad que la base. Redondea a dos cifras decimales.
cm²
cm²
Este campo es obligatorio.
La primera figura es un hexágono con una circunferencia circunscrita, por tanto el área pedida será el área del hexágono menos el área de la circunferencia.
Calculamos la apotema que es el radio de la circunferencia. Dado que el hexágono tiene lado podemos forma un triángulo equilatero de lados iguales a . La altura de este triángulo es nuestro radio, asi
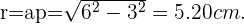
Dado que el perímetro mide 
, pues sumamos lados de tamaño . Podemos calcular el área del hexágono,
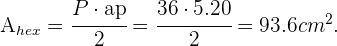
Ahora para el área del círculo tenemos que
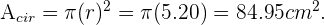
Finalmente el área de nuestra figura es la resta
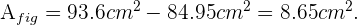
y además la necesitamos para el área del hexágono.
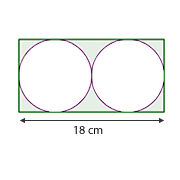
Para la segunda figura tenemos lo siguiente.
La altura del rectángulo es el diámetro de un circunferencia. De la figura podemos deducir que el diámetro mide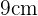 
, entonces el radio mide 
. Asi el área de una circunferencia es igual a
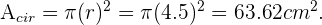
También podemos calcular el área del rectángulo, la cual es
Finalmente, notemos que el área de nuestra figura es igual al área del rectángulo menos el área de dos círculos, así
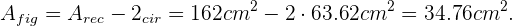
El radio mayor de un roscón de reyes es de 20 cm mientras que el radio menor mide 7 cm. Si cortamos un trozo con un ángulo de 20º, ¿qué área del roscón hemos cortado?.
cm²
Este campo es obligatorio.
Primero imaginemos el problema de la siguiente forma: Primero hallamos el área de un sector circular de radio 
con ángulo 
y luego hallamos el área de un sector circular de 
con ángulo . La resta de estas dos área nos dará el área del roscon.
Para el primer sector circular se tiene
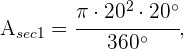
Para el segundo sector circular se tiene
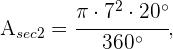
Finalmente, el área del roscón es
Calcular el área de la zona coloreada redondeando a dos cifras decimal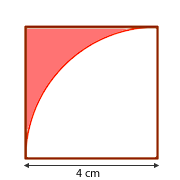
cm²
Este campo es obligatorio.
El área de nuestra región es la resta de un cuadrado de lado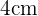 
menos el área de un cuarto de un circulo de radio .
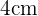Primero hallamos el área de un cuarto de circulo,
El área del cuadrado es
Finalmente, el área de nuestra figura es
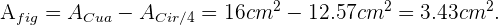
Si tienes dudas puedes consultar la teoría
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.