
Enunciado del Teorema de Pitágoras
El Teorema de Pitágoras establece lo siguiente:
En todo triángulo rectángulo el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.
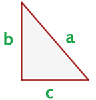
Del enunciado anterior se desprende la siguiente fórmula con la cual podemos calcular la magnitud de cada una de los lados de un triángulo rectángulo
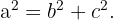
Aplicaciones del teorema de Pitágoras
Calculando la hipotenusa.
1 Conociendo los dos catetos podemos calcular la hipotenusa, solo debemos despejar la variable  de la ecuación
de la ecuación
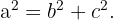
Lo hacemos simplemente sacando raíz cuadrada
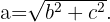
Ejemplo: Los catetos de un triángulo rectángulo miden en  y
y  respectivamente. ¿Cuánto mide la hipotenusa?
respectivamente. ¿Cuánto mide la hipotenusa?
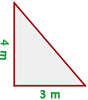
En este caso tenemos que 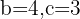 y debemos encontrar el valor de
y debemos encontrar el valor de 
Reemplazando en la fórmula anterior
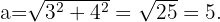
Por tanto la hipotenusa mide 
Calculando un cateto.
2 Conociendo la hipotenusa y un cateto, podemos calcular el otro cateto.
De nuestra ecuación inicial 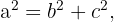 podemos despejar el valor de uno de los catetos y obtenemos lo siguiente para el cateto
podemos despejar el valor de uno de los catetos y obtenemos lo siguiente para el cateto 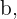
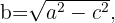
y para el cateto 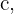

Ejemplo: La hipotenusa de un triángulo rectángulo mide 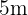 y uno de sus catetos
y uno de sus catetos  ¿Cuánto mide otro cateto?
¿Cuánto mide otro cateto?
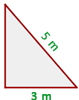
De acuerdo con la figura, tenemos que el cateto  mide
mide  , la hipotenusa
, la hipotenusa  y hace falta encontrar el cateto
y hace falta encontrar el cateto  . Así pues, utilizando la fórmula para calcular catetos,
. Así pues, utilizando la fórmula para calcular catetos,

Por lo tanto el cateto  mide
mide 
Clasificar triángulos rectángulos.
3. Conociendo los lados de un triángulo, podemos averiguar si es rectángulo o no.
Para que un triángulo sea rectángulo el cuadrado de lado mayor ha de ser igual a la suma de los cuadrados de los dos menores.
Ejemplo: Determinar si el siguiente triángulo es rectángulo.
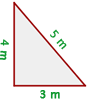
Notemos que el lado mayor de este triángulo tiene longitud  Continuando con la indicación anterior, habremos de verificar las siguientes igualdades
Continuando con la indicación anterior, habremos de verificar las siguientes igualdades
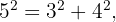
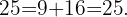
Ya que obtenemos el mismo resultado en ambos lados de la igualdad, podemos concluir que el triángulo es rectángulo.
Ejercicios
Un triángulo rectángulo isósceles tiene hipótenusa de 10 m de longitud. ¿Cuál es la longitud de sus catétos?
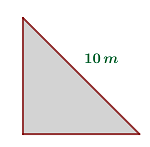
Como el triángulo es rectángulo e isósceles, entonces sus dos catétos son iguales. Aplicamos el Teorema de Pitágoras para el triángulo con hipótenusa  y lado
y lado 
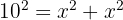
Resolviendo algebraicamente, se obtiene

Así, los catetos miden 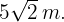
Una escalera de 10 m de longitud está apoyada sobre la pared. El pie de la escalera dista 6 m de la pared. ¿Qué altura alcanza la escalera sobre la pared?
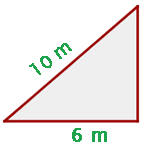
La escalera, la pared y el piso forman un triángulo rectángulo, en el cual podemos tomar como hipotenusa la longitud de la escalera y como uno de los catetos la longitud del pie de la escalera hasta la pared. Entonces  y
y 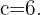
Nuestro objetivo es entonces, calcular la altura de escalera sobre la pared, es decir, calcular el cateto restante. De acuerdo con nuestras fórmulas anteriores y la figura, tenemos que

Hallar el área del triángulo equilátero:

Primero trazamos la altura del triángulo equilátero. Dicha altura divide el triángulo en dos triángulos rectángulos de catetos  la altura del triángulo equilátero,
la altura del triángulo equilátero,  la mitad de uno de los lados del triángulo y finalmente con hipotenusa
la mitad de uno de los lados del triángulo y finalmente con hipotenusa  , uno de los lados del triángulo inicial.De esta forma para hallar la altura solo debemos aplicar nuestra fórmula anterior para hallar catetos de triángulos rectángulo, lo que nos da
, uno de los lados del triángulo inicial.De esta forma para hallar la altura solo debemos aplicar nuestra fórmula anterior para hallar catetos de triángulos rectángulo, lo que nos da


Dado que el área de un triángulo se obtiene a través de la fórmula
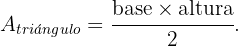
Observemos ahora, que la base del triángulo es de 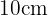 y la altura de
y la altura de 
Luego, remplazando en la fórmula del área se sigue que
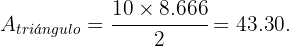
Hallar la diagonal del cuadrado:
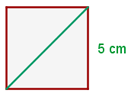
La diagonal del cuadrado cuyos lados miden 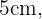 divide al dicha figura en dos triángulos rectángulos, donde la diagonal
divide al dicha figura en dos triángulos rectángulos, donde la diagonal  coincide con la hipotenusa de cualquiera de estos triángulos. Es decir, debemos hallar la hipotenusa de un triángulo rectángulo con catetos igual a
coincide con la hipotenusa de cualquiera de estos triángulos. Es decir, debemos hallar la hipotenusa de un triángulo rectángulo con catetos igual a 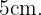
Para ello utilizaremos la fórmula para la hiptenusa:


Finalmente, la diagonal mide 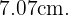
Hallar la diagonal del rectángulo:
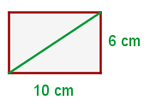
De manera similar al ejercicio anterior, la diagonal  de este rectángulo lo divide en dos triángulos rectángulos de catetos de
de este rectángulo lo divide en dos triángulos rectángulos de catetos de 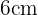 y
y 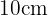 y la diagonal coincide con la hipotenusa de estos triángulos. Así que de nuevo debemos usar la fórmula para calcular la hipotenusa:
y la diagonal coincide con la hipotenusa de estos triángulos. Así que de nuevo debemos usar la fórmula para calcular la hipotenusa:
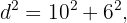
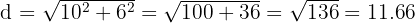
Por lo tanto, la diagonal tiene longitud 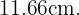
Hallar el perímetro y el área del trapecio rectángulo:

El perímetro del trapecio es la suma de la longitud de sus lados. De la figura se sigue que el lado superior del trapecio mide  el lado inferior mide
el lado inferior mide 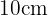 y la altura del trapecio mide
y la altura del trapecio mide  Para hallar el lado diagonal del trapecio, que llamaremos
Para hallar el lado diagonal del trapecio, que llamaremos 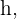 debemos considerar el triángulo rectángulo de lado vertical
debemos considerar el triángulo rectángulo de lado vertical  lado horizontal
lado horizontal 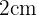 e hipotenusa
e hipotenusa 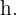 Dado que necesitamos calcular el valor de
Dado que necesitamos calcular el valor de 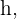 utilizaremos la fórmula para calcular la hipotenusa, asi pues tenemos:
utilizaremos la fórmula para calcular la hipotenusa, asi pues tenemos:
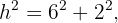
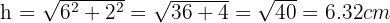
Finalmente podemos calcular el perímetro, el cual sabemos que es igual a la suma
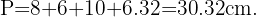
Para obtener el área hay que observar que el trapecio está conformado por un triángulos rectángulos y un rectángulo, entonces su área será igual a la suma de las áreas del triángulo y el rectángulo. Es decir,
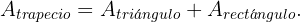
El área del rectángulo es sencillamente el producto de su base por su altura, entonces  Para el área del triángulo tenemos que
Para el área del triángulo tenemos que
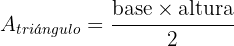

Por lo tanto

El perímetro de un trapecio isósceles es de 110 m, las bases miden 40 y 30 m respectivamente. Calcular los lados no paralelos y el área.
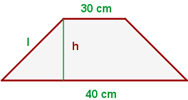
El perímetro del trapecio es igual a la suma de la longitud de sus lados. Entonces tenemos la siguiente igualdad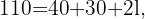 donde
donde  es el valor del lado no paralelo.Despejando
es el valor del lado no paralelo.Despejando  de la anterior ecuación, tenemos que
de la anterior ecuación, tenemos que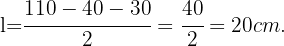 De esta forma hemos resuelto la primera parte del problema.
De esta forma hemos resuelto la primera parte del problema.
Recordemos que el área del trapecio es igual a la suma de las bases, multiplicadas por la altura y luego esto se divide entre dos. Así que debemos calcular la altura del trapecio, que llamaremos 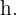
De la figura podemos considerar el triángulo rectángulo de catetos 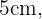
 e hipotenusa
e hipotenusa 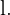 Luego, para hallar el valor de
Luego, para hallar el valor de  , utilizaremos la fórmula para calcular los catetos,
, utilizaremos la fórmula para calcular los catetos,
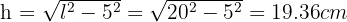
Ahora podemos concluir calculando el área del trapecio,
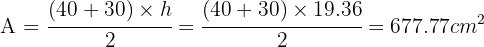
Hallar el área del pentágono regular:

Tenemos que los lados del pentágono regular miden  Ya que el área del pentágono es igual a un medio del perímetro por el valor del apotema, entonces debemos encontrar el valor del apotema. Llamaremos al apotema
Ya que el área del pentágono es igual a un medio del perímetro por el valor del apotema, entonces debemos encontrar el valor del apotema. Llamaremos al apotema 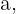 tal como se ilustra en la figura. Para calcular
tal como se ilustra en la figura. Para calcular 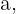 consideremos el triángulo de catetos
consideremos el triángulo de catetos 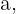
 e hipotenusa
e hipotenusa 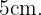 Y utilizamos la fórmula para calcular catetos, entonces:
Y utilizamos la fórmula para calcular catetos, entonces:
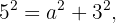
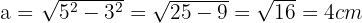
El valor del perímetro del pentágono es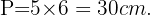
Finalmente, podemos calcular el área del pentágono
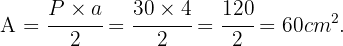
Calcular el área del cuadrado inscrito en una circunferencia de longitud 18.84 m.
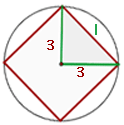
Ya que el cuadrado esta inscrito una circunferencia, entonces podemos dividirlo en  triángulos rectángulos de catetos igual al radio del a circunferencia,
triángulos rectángulos de catetos igual al radio del a circunferencia,  , e hiputenusa
, e hiputenusa  .De esta forma podemos calcular el lado del triángulo utilizando la fórmula para calcular hipotenusas,
.De esta forma podemos calcular el lado del triángulo utilizando la fórmula para calcular hipotenusas,
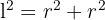
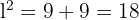 .
.
Por lo tanto, como el área del cuadrado es 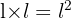 se sigue que es igual a
se sigue que es igual a 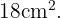
En una circunferencia una cuerda mide 48 cm y dista 7 cm del centro. Calcular el área del círculo.
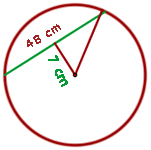
Para calcular el área del circulo debemos primero encontrar su radio. Ya que la cuerda del circulo dista  del centro, podemos formar un triángulo rectángulo de catetos
del centro, podemos formar un triángulo rectángulo de catetos  , la mitad de la cuerda,
, la mitad de la cuerda, 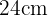 e hipotenusa igual al radio del circulo,
e hipotenusa igual al radio del circulo,  . De esta forma, para hallar el radio debemos utilizar la fórmula para calcular hipitenusas.
. De esta forma, para hallar el radio debemos utilizar la fórmula para calcular hipitenusas.
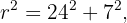
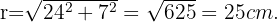
Así, el area del círculo es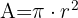

Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.