Resuelve los siguientes problemas:
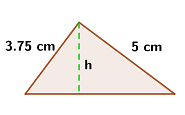
Calcula la altura de un triángulo rectángulo con los datos que se muestran en la figura: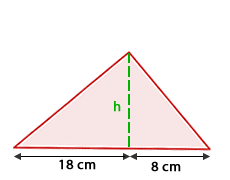 
Este campo es obligatorio.
1 Aplicando el teorema de la altura: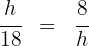 
2 Despejamos 
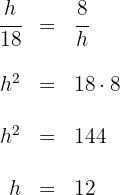
La altura buscada es
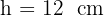
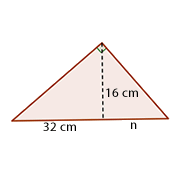
Calcula la altura de un triángulo rectángulo con los datos que se muestran en la figura:
Este campo es obligatorio.
1 Aplicando el teorema de la altura: 
2 Despejamos 
La altura buscada es
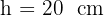
En un triángulo rectángulo, la altura correspondiente a la hipotenusa mide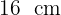 
y la proyección ortogonal de uno de sus catetos mide 
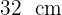. ¿Cuánto mide la hipotenusa de dicho triángulo?
.
Este campo es obligatorio.
1Representamos el problema de forma gráfica
2Aplicando el teorema de la altura se tiene que: 
Luego, la otra proyección mide 
.
3Por tanto, la hipotenusa mide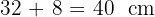 
.
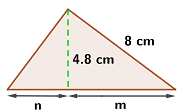
En un triángulo rectángulo, la altura correspondiente a la hipotenusa mide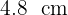 
y su cateto mayor mide . ¿Cuánto mide la hipotenusa de dicho triángulo?
.
Este campo es obligatorio.
1Representamos el problema de forma gráfica
2Aplicando el teorema de Pitágoras se obtiene: 
Luego, la otra proyección del cateto conocido mide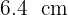 
.
3Aplicando el teorema de la altura se tiene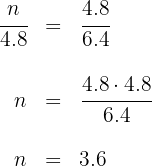 
4Por tanto, la hipotenusa mide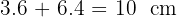 
.
En un triángulo rectángulo, sus cateto miden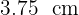 
y 
. ¿Cuánto mide la altura correspondiente a la hipotenusa de dicho triángulo?
.
Este campo es obligatorio.
1Representamos el problema de forma gráfica
2Aplicando el teorema de Pitágoras se obtiene: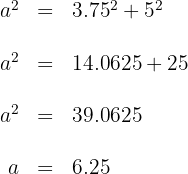 
Luego, la hipotenusa mide 
. 
3Aplicando el teorema del cateto se tiene 
Luego, la otra proyección mide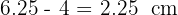 
.
4Aplicamos el teorema de la altura 
Luego, la altura mide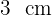 
.
6 Se inscribe un triángulo rectángulo en una circunferencia de radio cuyo lado 
mide 
, quedando como muestra la figura.
Calcula la longitud de la hipotenusa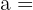 
.
Este campo es obligatorio.
En una circunferencia, para cualquier triángulo rectángulo inscrito su hipotenusa es igual al diámetro de la circunferencia, entonces la hipotenusa mide 
¿Cuál debe ser la longitud del lado faltante?
.
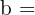
Este campo es obligatorio.
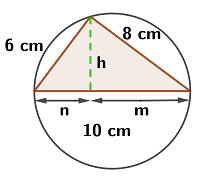
Aplicando el teorema de Pitágoras se obtiene: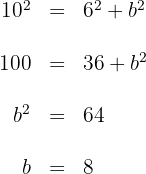 
¿Sabrías decir cuál es la altura respecto a la hipotenusa?
.
Este campo es obligatorio.
Aplicando el teorema del cateto se tiene
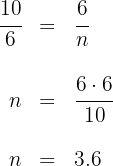
Luego la otra proyección mide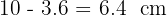 
Aplicando el teorema de la altura se tiene
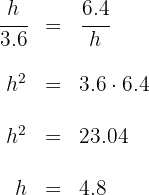
7Una maqueta de barco usa dos cablecitos para tensar el mástil mayor, debiendo quedar como muestra la figura.
Calcula la distancia a la que debemos colocar el cable . .
Este campo es obligatorio.
En primer lugar observemos que se trata de un triángulo rectángulo, por lo que podemos aplicar el teorema del cateto y de la altura.
Aplicamos el teorema del cateto para calcular la distancia a la que se debe encontrar el segundo cable:
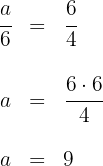
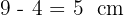
Debemos colocar el segundo cable a de distancia de la base de mástil.
¿Cuál debe ser la longitud de dicho cable?
.
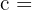
Este campo es obligatorio.
Aplicamos el teorema del cateto para calcular la medida del lado :
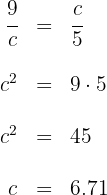
La medida del lado es de 
¿Sabrías decir cuál es la altura del mástil?
.
Este campo es obligatorio.
Aplicamos el teorema de la altura para calcular la altura del mástil:
El mástil tiene una altura de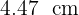 
8Observa el tobogán en el que juegan Lucía y Marcos. Calcula la medida del lado 
.
.
Este campo es obligatorio.
En primer lugar observemos que se trata de un triángulo rectángulo, por lo que podemos aplicar el teorema del cateto y de la altura.
Aplicamos el teorema del cateto para calcular la medida de . 
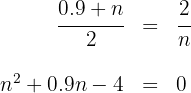
Resolvemos la ecuación cuadrática 
Se obtienen las raíces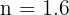 
y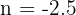 
De las dos soluciones obtenidas sólo es válida la solución positiva, pues el dato que buscamos es una medida, que no puede ser negativa. Por tanto, la distancia pedida es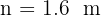 
¿Cuál es la altura del tobogán? .
Este campo es obligatorio.
Usamos el teorema de la altura para calcular la altura del tobogán.
Luego, la altura del tobogán es de 
.
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.