Capítulos
Elementos de un polígono
Un polígono es la región del plano limitada por tres o más segmentos, y los elementos de un polígono son:
1 Lados: los segmentos que lo limitan.
2 Vértices: puntos donde concurren dos lados.
3 Ángulos interiores: son aquellos que quedan determinados por dos lados consecutivos.
Una propiedad interesante que cumplen los ángulos interiores de un polígono de 
lados es que, si formamos triángulos al interior del polígono, la suma de todos los ángulos interiores de dichos triángulos se puede obtener a través de la siguiente fórmula
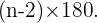
En esta fórmula,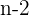 
representa la cantidad de triángulos que podemos formar y, agregamos el factor 
sabiendo que es la suma de los los ángulos internos de un triángulo.
4Diagonal: cualquier segmento determinado por dos vértices no consecutivos.
Para un polígono de lados, se puede calcular el número de diagonales con la fórmula
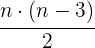
Hay varias maneras de clasificar a los polígonos y la primera que estudiaremos es la clasificación que surge al tener en cuenta el número de lados.
Clasificación de los polígonos por número de lados
Triángulos
Tienen 3 lados.
Cuadriláteros
Tienen 4 lados.
Pentágonos
Tienen 5 lados.
Hexágonos
Tienen 6 lados.
Heptágonos
Tienen 7 lados.
Octágonos
Tienen 8 lados.
Eneágono
Tienen 9 lados.
Decágono
Tienen 10 lados.
Endecágono
Tienen 11 lados.
Dodecágono
Tienen 12 lados.
Tridecágono
Tienen 13 lados.
Tetradecágono
Tienen 14 lados.
Pentadecágono
Tienen 15 lados.
Hexadecágono
Tienen 16 lados.
Heptadecágono
Tienen 17 lados.
Octadecágono
Tienen 18 lados.
Eneadecágono
Tienen 19 lados.
Icoságono
Tienen 20 lados.
Clasificación de los polígonos por sus ángulos
La clasificación de los polígonos a través de sus ángulos hace referencia a la medida que alcanzan los ángulos interiores.
Convexos
Los polígonos convexos serán aquellos cuya medida de cualquier ángulo interior esté por debajo de 180° y todas sus diagonales serán interiores.
Cóncavos
Denominaremos como convexo a un polígono si la medida de algún ángulo interno es mayor a 180° o si una de sus diagonales es exterior.
Polígonos regulares
Un polígono regular es aquel que tiene sus ángulos internos iguales y sus lados son de igual longitud.
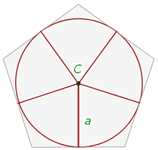
Elementos de un polígono regular
1 Centro: es el punto interior que equidista de cada vértice.
2 Radio: segmento que va del centro a cada vértice.
3 Apotema: distancia del centro al punto medio de un lado.
4Ángulo central: ángulo formado por dos radios consecutivos.
lados, las siguientes fórmulas son válidas. 
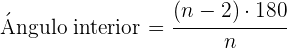
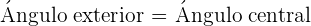
Polígonos inscritos
Diremos que un polígono está inscrito en una circunferencia si todos sus vértices están contenidos en ella.
Circunferencia circunscrita
Llamaremos circunferencia circunscrita a la única circunferencia que toca a todos los vértices del polígono, su centro equidista de todos los vértices y su radio coincide con el radio del polígono.
Circunferencia inscrita
Llamaremos circunferencia inscrita a la única circunferencia que toca en el punto medio de cada lado del polígono, su centro equidista de todos los lados y su radio coincide con el apotema del polígono.
Tipos de triángulos
Como mencionamos al inicio del artículo, un triángulo es un polígono con tres lados. Para este tipo de polígonos, tenemos que se cumplen las siguientes afirmaciones.
1 Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.
2 La suma de los ángulos interiores de un triángulo es igual a 180°.
3 El valor de un ángulo exterior es igual a la suma de los dos interiores no adyacentes.
Podemos clasificar los triángulos de acuerdo a la relación que guardan sus lados.
Triángulo equilátero
Llamaremos triángulo equilátero a un triángulo con sus tres lados con igual magnitud.
Triángulo isósceles
Llamaremos triángulo equilátero a un triángulo con solo dos de sus lados de igual magnitud.
Triángulo escaleno
El triángulo escaleno será aquel que tenga todos sus lados de distintas magnitudes.
La siguiente clasificación estará definida por sus ángulos.
Triángulo acutángulo
Triángulo con tres ángulos agudos.
Triángulo rectángulo
Triángulo con ángulo recto. En este tipo de triángulo es válido el Teorema de Pitágoras y bajo este contexto, la hipotenusa será el lado de mayor longitud, mientras que los lados menores serán los catetos.
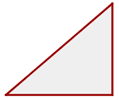
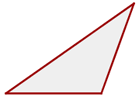
Triángulo obtusángulo
Llamaremos obtusángulo a un triángulo con al menos un ángulo obtuso.
Lugares geométricos importantes en un triángulo
Alturas de un triángulo
Se llama altura a cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o su prolongación).
Ortocentro
Es el punto de intersección de las tres alturas.
Medianas de un triángulo
Mediana es cada una de las rectas que une el punto medio de un lado con el vértice opuesto.
Baricentro
Se llama baricentro al punto de intersección de las tres medianas. Dicho punto divide a cada mediana en dos segmentos con la siguiente propiedad: el segmento que une el baricentro con el vértice mide el doble que el segmento que une baricentro con el punto medio del lado opuesto. En el contexto de la imagen siguiente esto se traduce como
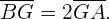
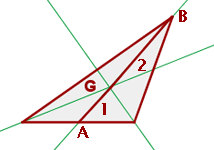
Mediatrices de un triángulo
Mediatriz es cada una de las rectas perpendiculares trazadas a un lado por su punto medio.
Circuncentro
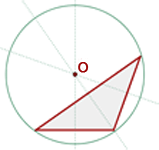
Bisectrices de un triángulo
Bisectriz es cada una de las rectas que divide a un ángulo interno en dos ángulos iguales.
Incentro
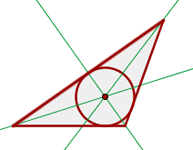
Es el punto de intersección de las tres bisetrices y el centro de una circunferencia inscrita en el triángulo.
Recta de Euler
Para un triángulo no equilátero, el ortocentro, el baricentro y el circuncentro son colineales; es decir, existe una recta a la cual pertenecen los tres, dicha recta es conocida como la recta de Euler.
Clasificación de cuadriláteros
Llamamos cuadriláteros a aquellos polígonos que tienen cuatro lados. Para estos polígonos tenemos que la suma de sus ángulos interiores es igual a 360°.
Paralelogramos
Estos polígonos son aquellos cuadriláteros que tienen los lados paralelos dos a dos y se clasifican en:
Cuadrado
Con 4 lados iguales y los 4 ángulos interiores rectos.
Rectángulo
Tiene lados iguales dos a dos y los 4 ángulos iternos son rectos.
Rombo
Tiene los cuatro lados iguales.
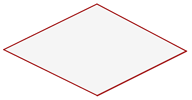
Romboide
Tiene lados iguales dos a dos.
Trapecios
Cuadriláteros que tienen solo dos lados paralelos, los cuales son llamados base mayor y base menor. Estos se clasifican en:
Trapecio rectángulo
Trapecio con un ángulo interior recto.
Trapecio isósceles
Trapecio con dos lados no paralelos iguales.
Trapecio escaleno
No tiene ningún lado igual ni ángulo recto.
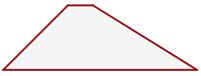
Trapezoides
Cuadriláteros que no tiene ningún lado igual ni paralelo.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
8 Un rectángulo tiene un ancho de 3 unidades. El largo del rectángulo es 5 veces su ancho. ¿Cuál es el área del rectángulo?
45u²
unidades
El largo es
Ahora bien, su área es
hola
No,entiendo si estoy poniendo bien el resultado por que me dice que esta mal ? si,estoy poniendo el resultado que aparece en la solución ya lo corregi 5 veces esta mal copiado ? por favor me dicen cual es el problema
Hola tienes razón, tu resultado es correcto, pero en este momento estamos remodelando la pagina y corriendo errores así que pronto vamos a corregir este que mencionas.
Todo bien con los otros ejercicios pero no me fue posible realizar el 1 y 2
Hola estamos a tu disposición para cualquier duda, solo menciona de manera especifica donde te atoras y con gusto te ayudamos.
Hola, soy Clarisa Israel, Ingeniera en Construcciones. Entiendo que el Romboide es un cuadrilátero con caracteristicas especiales y su nombre indica que tiene un parecido con el Rombo. Ese parecido tiene que ver con que sus diagonales son perpendiculares, y se cortan en el punto medio de una de ellas pero no de la otra. De esa manera al unir los puntos, 2 de sus lados consecutivos resultan de igual longitud y los 2 restantes también tienen igual longitud pero distinta a la de los primeros. NO es un paralelogramo pues sus lados opuestos no son paralelos. Tiene la típica forma de un Barrilete.
El material del sitio me parece muy interesante!!
Espero consideren este comentario.
Atentamente
Hola muchas gracias por tu aportación, lo tomaremos en cuenta para mejorar en nuestro contenido.
Se cumple que BM = MC y AQ = QM con A – Q – M y B – M − C. Si a(ABQ) = 8 ul^2, determine el área del ∆ABC.
No me deja poner 45u²
Hola puedes hacernos el favor de decirnos el número de ejercicio para poder corregirlo.