Ejercicios propuestos. Resuelve los siguientes ejercicios sobre la circunferencia y el circulo :
m del centro de una plataforma que gira y su amiga Laura se ha montado en el león que estaba a 
m del centro. Calcular el camino recorrido por cada una cuando la plataforma ha dado 
vueltas.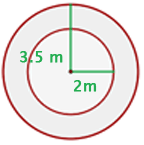
Queremos la cantidad recorrida por cada una cuando se dan las 50 vueltas. Para esto necesitamos el perímetro del circulo, pues la cantidad recorrida en una vuelta seria el perímetro del circulo.
Recordemos que el perímetro de un circulo es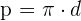 
donde 
perímetro, y 
diámetro.
Camino recorrido por Ana:
entonces en 50 vueltas 
Camino recorrido por Laura: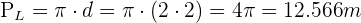 
entonces en 50 vueltas
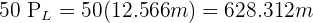
Los brazos de un columpio miden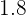 
m de largo y pueden describir como máximo un ángulo de 
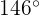. Calcula el espacio recorrido por el asiento del columpio cuando el ángulo descrito en su balanceo es el máximo.
En este caso no calculamos el perímetro completo puesto que no se recorre la circunferencia completa, solo se recorren 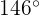de los 
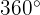, por lo tanto la distancia recorrida seria :
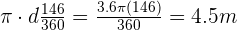
cm el radio de la circunferencia.
Notemos en la figura que el segmento circular es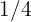 
de el circulo completo, por lo tanto, calculamos un cuarto del área completa
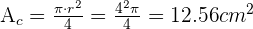
Calcula el área sombreada, sabiendo que el lado de cuadrado es 
cm y el radio del círculo mide 
cm.
Para resolver el ejercicio debemos calcular el área
Área circulo del cuadrado y después proceder restando el área del circulo para encontrar el área sombreada:
Área cuadrado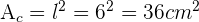 
Por lo tanto el area sombreada es :
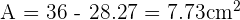
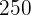m se van a poner 
farolas cuyas bases son círculos de 
m de radio, el resto de la plaza lo van a utilizar para sembrar césped. Calcula el área del césped.
Para encontrar el área sombreada de la figura debemos calcular el área del circulo y restarle el área ocupada por los 7 faros. Área de los 7 faros:
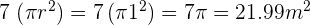Área del circulo: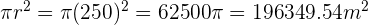 
Área sombreada:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
8 Un rectángulo tiene un ancho de 3 unidades. El largo del rectángulo es 5 veces su ancho. ¿Cuál es el área del rectángulo?
45u²
unidades
El largo es
Ahora bien, su área es
hola
No,entiendo si estoy poniendo bien el resultado por que me dice que esta mal ? si,estoy poniendo el resultado que aparece en la solución ya lo corregi 5 veces esta mal copiado ? por favor me dicen cual es el problema
Hola tienes razón, tu resultado es correcto, pero en este momento estamos remodelando la pagina y corriendo errores así que pronto vamos a corregir este que mencionas.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.