La circunferencia y el círculo son conceptos fundamentales en geometría, esenciales tanto en el estudio teórico de las matemáticas como en aplicaciones prácticas. La circunferencia se define como el conjunto de puntos que están a una distancia fija, llamada radio, desde un punto central. Por su parte, el círculo es la región delimitada por la circunferencia y contiene todos los puntos que se encuentran a una distancia menor o igual al radio.
Tanto el círculo como la circunferencia se encuentran en la naturaleza y en la vida cotidiana, desde la forma de los planetas y órbitas hasta estructuras arquitectónicas, ruedas y muchos mecanismos de precisión. Por esta razón, comprender sus propiedades y aprender a calcular medidas como la longitud, área, diámetros, y arcos resulta muy valioso para desarrollar una comprensión sólida de la geometría
Encuentra el perímetro de una circunferencia cuyo radio mide 5.3 cm
1Recordemos que la fórmula para el perímetro (o longitud) de una circunferencia es:
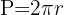
2Sustituimos los datos conocidos y obtenemos
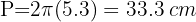
Calcula el área de un círculo con radio de 11 cm
1Recordemos que la fórmula para el área de un círculo es:

2Sustituimos los datos conocidos y obtenemos
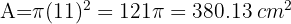
Halla la longitud de un arco de 100° en una circunferencia de radio 9 cm
1Recordemos que la fórmula para la longitud de arco de una circunferencia es:
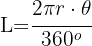
2Sustituimos los datos conocidos y obtenemos
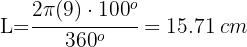
En una circunferencia de radio 10 cm, un arco mide 15 cm. ¿Cuál es el ángulo central subtendido por el arco?
1Recordemos que la fórmula para la longitud de arco de una circunferencia es:
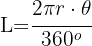
2Sustituimos los datos conocidos, despejamos el ángulo y obtenemos
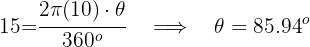
Encuentra el área de un sector circular con ángulo central de 60° y radio 7 cm
1Recordemos que la fórmula para el área de un sector es:
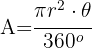
2Sustituimos los datos conocidos y obtenemos
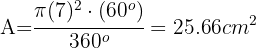
Si el perímetro de una circunferencia es 70 cm, encuentra su diámetro
1Recordemos que la fórmula para el perímetro de una circunferencia es:
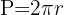
2Sustituimos los datos conocidos, despejamos el radio y obtenemos
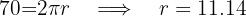
Así, el diámetro es 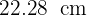
Si el área de un círculo es 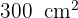 , encuentra su diámetro
, encuentra su diámetro
1Recordemos que la fórmula para el área de un círculo es:

2Sustituimos los datos conocidos, despejamos el radio y obtenemos
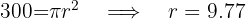
Así, el diámetro es 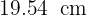
En una circunferencia de radio 17 cm, dos puntos A y B están separados por un ángulo de 80° respecto al centro. ¿Cuál es la distancia entre A y B medidos sobre la circunferencia?
1Recordemos que la fórmula para la longitud angular es:
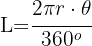
2Sustituimos los datos conocidos y obtenemos
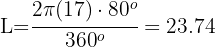
Así, la distancia de A a B sobre la circunferencia es 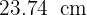
Encuentra la distancia desde el punto (7,2) a la circunferencia con centro en (0,0) y radio 3
1Calculamos la distancia entre el punto y el centro de la circunferencia
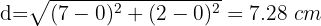
2Luego la distancia entre el punto y la circunferencia es
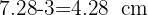
Los brazos de un columpio miden 1.8 m de largo y pueden describir como máximo un ángulo de 146°. Calcula el espacio recorrido por el asiento del columpio cuando el ángulo descrito en su balanceo es el máximo
1Calculamos el recorrido para 
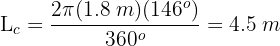
La rueda de un camión tiene 90 cm de radio. ¿Cuánto ha recorrido el camión cuando la rueda ha dado 100 vueltas?
1Convertimos el radio a metros

2Calculamos el recorrido de una vuelta
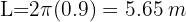
3Calculamos el recorrido para 100 vueltas

Un faro barre con su luz un ángulo plano de 128°. Si el alcance máximo del faro es de 7 millas, ¿cuál es la longitud máxima en metros del arco correspondiente?
1Convertimos el radio a metros, sabiendo que una milla equivale a 1609.34 metros
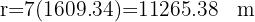
2Calculamos el recorrido para 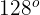
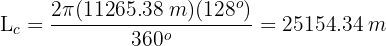
La longitud de una circunferencia es 43.96 cm. ¿Cuál es el área del círculo?
1Calculamos el radio de la circunferncia

2Calculamos el área del círculo
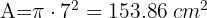
El área de un sector circular de 90° es 4π cm cuadrados. Calcular el radio del círculo al que pertenece y la longitud de la circunferencia
1Calculamos el radio del sector
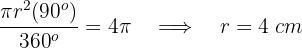
2Calculamos la longitud de la circunferencia
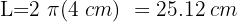
Ana se ha montado en el caballo que está a 3.5 m del centro de una plataforma que gira y su amiga Laura se ha montado en el león que estaba a 2 m del centro. Calcular el camino recorrido por cada una cuando la plataforma ha dado 50 vueltas
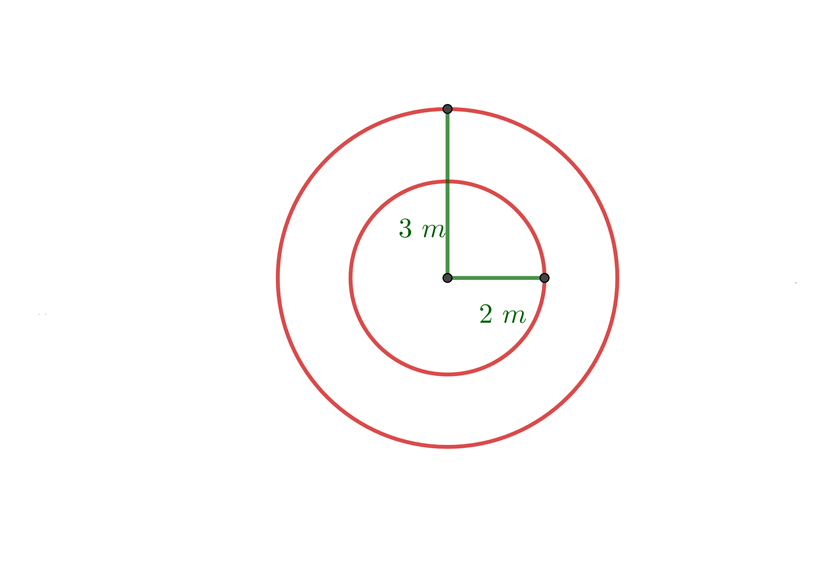
1Calculamos el recorrido de una vuelta con 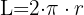


2El recorrido total se obtiene multiplicando una vuelta por 50
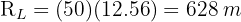

Hallar el área de un sector circular cuya cuerda es el lado del triángulo equilátero inscrito, siendo 2 cm el radio de la circunferencia

1El sector solicitado corresponde a una tercera parte del área total del círculo, esto es, un sector de 
2Calculamos el área para 

Dadas dos circunferencias concéntricas de radio 8 y 5 cm respectivamente, se trazan los radios OA y OB, que forman un ángulo de 60°. Calcular el área del trapecio circular formado

1Calculamos el área de los dos sectores y luego la diferencia de estos.

En un parque de forma circular de 700 m de radio hay situada en el centro una fuente, también de forma circular, de 5 m de radio. Calcula el área de la zona de paseo

1Calculamos el área de los dos sectores y luego la diferencia de estos.
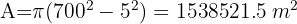
La superficie de una mesa está formada por una parte central cuadrada de 1 m de lado y dos semicírculos adosados en dos lados opuestos. Calcula el área

1Calculamos el área del cuadrado y del círculo formado por los dos semicirculos y luego la suma de estos.
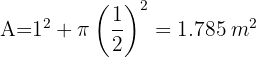
Hallar el área del sector circular cuya cuerda es el lado del cuadrado inscrito, siendo 4 cm el radio de la circunferencia
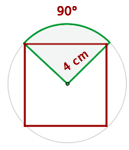
1Calculamos el área para el sector de 
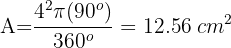
Calcula el área sombreada, sabiendo que el lado de cuadrado es 6 cm y el radio del círculo mide 3 cm

1Calculamos el área del cuadrado y del círculo y luego la diferencia de estos

En una plaza de forma circular de radio 250 m se van a poner 7 farolas cuyas bases son círculos de un 1 m de radio, el resto de la plaza lo van a utilizar para sembrar césped. Calcula el área del césped

1Calculamos el área del círculo mayor, de las farolas y luego la diferencia de estos.

Calcula el área de la parte sombreada, si el radio del círculo mayor mide 6 cm y el radio de los círculos pequeños miden 2 cm 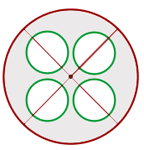
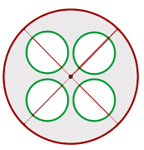
1Calculamos el área del círculo mayor, de los círculos menores y luego la diferencia de estos
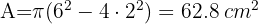
Calcula el área de la parte sombreada, siendo AB = 10 cm, ABCD un cuadrado y APC Y AQC arcos de circunferencia de centros B y D 
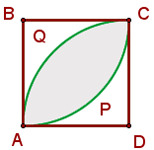
1La parte sombreada se compone de dos segmentos circulares:
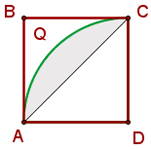
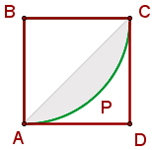
2Calculamos el área del segmento circular y lo multiplicamos por 2
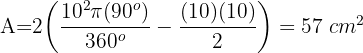
A un hexágono regular 4 cm de lado se le inscribe una circunferencia y se le circunscribe otra. Hallar el área de la corona circular así formada
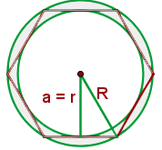
1Calculamos el radio del círculo interior el cual coincide con la apotema del hexágono

2Calculamos el área de cada círculo y luego la diferencia de estos
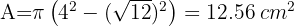
En una circunferencia una cuerda de 48 cm y dista 7 cm del centro. Calcular el área del círculo
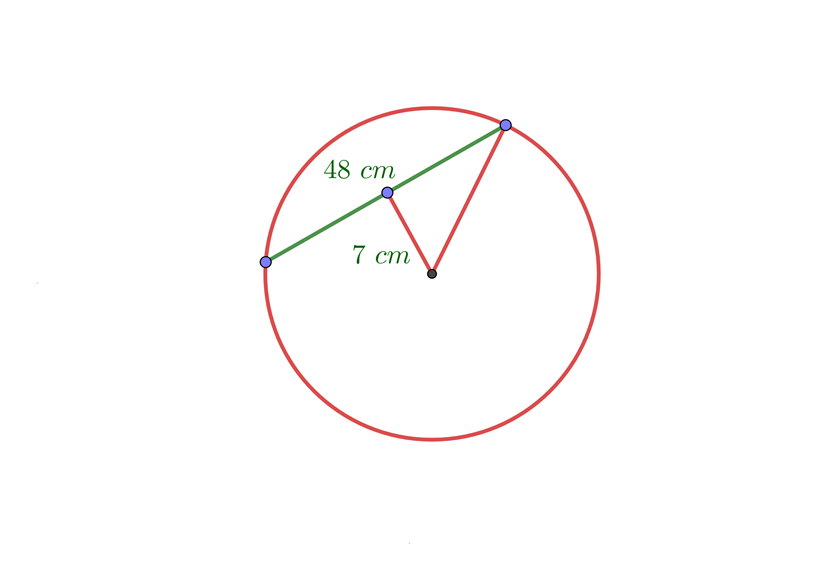
1Calculamos el radio del círculo aplicando el teorema de Pitágoras
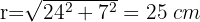
2Calculamos el área del círculo
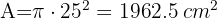
Los catetos de un triángulo inscrito en una circunferencia miden 22.2 cm y 29.6 cm respectivamente. Calcular el área del círculo
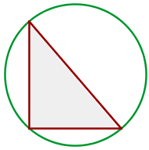
1Calculamos la hipotenusa, la cual es el diámetro de la circunferencia
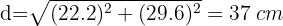
2Calculamos el área de cada círculo
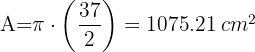
Sobre un círculo de 4 cm de radio se traza un ángulo central de 60°. Hallar el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente
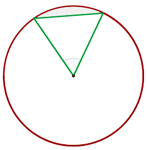
1Calculamos el área del sector
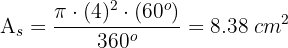
2Calculamos la altura del triángulo y el área del mismo


3Calculamos la diferencia de áreas
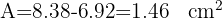
Dado un triángulo equilátero de 6 m de lado, hallar el área de uno de los sectores determinado por la circunferencia circunscrita y por los radios que pasan por los vértices
1El centro de la circunferencia es el baricentro. Por tanto 

2Calculamos la altura del triángulo y el radio
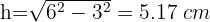

3Calculamos el área del sector
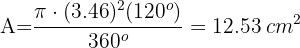
Calcular el área de la corona circular determinada por las circunferencias inscrita y circunscrita a un cuadrado de 8 m de diagonal

1Calculamos el radio del círculo exterior, cuyo diámetro es la diagonal del cuadrado y el radio del círculo interior mediante el Teorema de Pitágoras
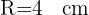

2Calculamos las diferencias de áreas
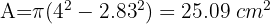
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.