Definición de circunferencia
Una circunferencia es una línea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo llamado centro, como se muestra en la siguiente figura.
Elementos de la circunferencia
Centro de la circunferencia
Punto del que equidistan todos los puntos de la circunferencia.
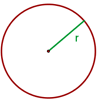
Radio de la circunferencia
Segmento que une el centro de la circunferencia con un punto cualquiera de la misma.
Cuerda
Segmento que une dos puntos de la circunferencia.
Diámetro
Cuerda que pasa por el centro de la circunferencia.
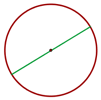
Arco
Un arco de circunferencia es cada una de las partes en que una cuerda divide a la circunferencia.
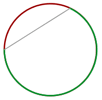
Semicircunferencia
Cada uno de los arcos iguales que abarca un diámetro.
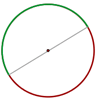
Longitud de una circunferencia
Esta dada por la fórmula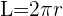 
Longitud de un arco de circunferencia
Se suele vincular a cada cuerda el menor arco que delimita.
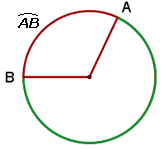
Un arco de circunferencia se denota con el símbolo
Las letras se escriben en sentido antihorario, es decir, en contra de las agujas del reloj.
Longitud de un arco de circunferencia
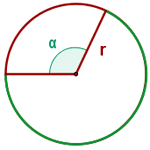
Esta dada por la fórmula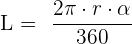 
Ejercicios de circunferencia
La longitud de una circunferencia es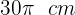 
. encuentra el radio.
Aplicamos la fórmula de la longitud de la circunferencia
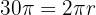
Despejando el radio se obtiene
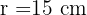
Calcular la longitud de una rueda de 90 cm de diámetro.
La circunferencia que tenemos es la siguiente
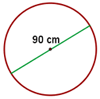
Para poder aplicar la formula necesitamos conocer el radio, es decir,
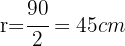
Ahora aplicando la fórmula de la longitud de la circunferencia
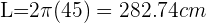
Calcular el área del cuadrado inscrito en una circunferencia de longitud 18.84 cm.
Dada la siguiente figura
y sustituyendo los datos en la fórmula de la longitud de la circunferencia
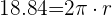
Podemos despejar el radio para así calcular el valor de los lados del cuadrado
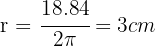
Aplicando el teorema de pitágoras
Por lo tanto, el área del cuadrado inscrito en la circunferencia es
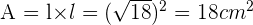
Los brazos de un columpio miden 1.8 m de largo y pueden describir como máximo un ángulo de 146°. Calcula el espacio recorrido por el asiento del columpio cuando el ángulo descrito en su balanceo es el máximo.
Sustituimos los valores en la fórmula directamente
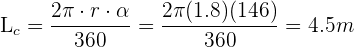
Un faro barre con su luz un ángulo plano de 128°. Si el alcance máximo del faro es de 7 millas, ¿cuál es la longitud máxima en metros del arco correspondiente?
Considerando que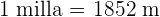 
y sustituyendo en la fórmula
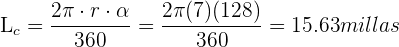
Por último, convertimos las millas a metros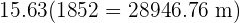
Ángulos en la circunferencia
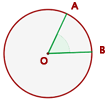
Ángulo central
El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.
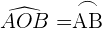
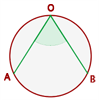
Ángulo inscrito
El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.
Mide la mitad del arco que abarca.
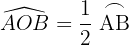
Ángulo semiinscrito
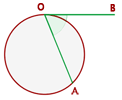
El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella.
Mide la mitad del arco que abarca.
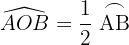
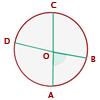
Ángulo interior
Su vértice es interior a la circunferencia y sus lados secantes a ella.
Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.
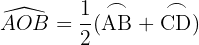
Ángulo exterior
Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:
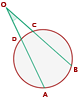
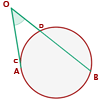
Mide la mitad de la diferencia entre las medidas de los arcos que abarcan sus lados sobre la circunferencia.
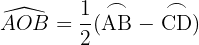
¿Quieres encontrar el profesor de matematicas ideal? Superprof es tu sitio.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
8 Un rectángulo tiene un ancho de 3 unidades. El largo del rectángulo es 5 veces su ancho. ¿Cuál es el área del rectángulo?
45u²
unidades
El largo es
Ahora bien, su área es
hola
No,entiendo si estoy poniendo bien el resultado por que me dice que esta mal ? si,estoy poniendo el resultado que aparece en la solución ya lo corregi 5 veces esta mal copiado ? por favor me dicen cual es el problema
Hola tienes razón, tu resultado es correcto, pero en este momento estamos remodelando la pagina y corriendo errores así que pronto vamos a corregir este que mencionas.
Todo bien con los otros ejercicios pero no me fue posible realizar el 1 y 2
Hola estamos a tu disposición para cualquier duda, solo menciona de manera especifica donde te atoras y con gusto te ayudamos.
Hola, soy Clarisa Israel, Ingeniera en Construcciones. Entiendo que el Romboide es un cuadrilátero con caracteristicas especiales y su nombre indica que tiene un parecido con el Rombo. Ese parecido tiene que ver con que sus diagonales son perpendiculares, y se cortan en el punto medio de una de ellas pero no de la otra. De esa manera al unir los puntos, 2 de sus lados consecutivos resultan de igual longitud y los 2 restantes también tienen igual longitud pero distinta a la de los primeros. NO es un paralelogramo pues sus lados opuestos no son paralelos. Tiene la típica forma de un Barrilete.
El material del sitio me parece muy interesante!!
Espero consideren este comentario.
Atentamente
Hola muchas gracias por tu aportación, lo tomaremos en cuenta para mejorar en nuestro contenido.
Se cumple que BM = MC y AQ = QM con A – Q – M y B – M − C. Si a(ABQ) = 8 ul^2, determine el área del ∆ABC.
No me deja poner 45u²
Hola puedes hacernos el favor de decirnos el número de ejercicio para poder corregirlo.