Resuelve los siguientes problemas:
Hallar el área de la siguiente figura:
El área pedida es de cm².
Este campo es obligatorio.
En primer lugar calculamos las medidas que faltan, para poder triangular la figura:
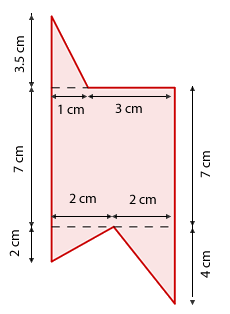
Ahora distinguimos los tres triángulos que podemos apreciar y el rectángulo central y hallamos el área de cada uno de ellos. El área total será igual a la suma de todas ellas.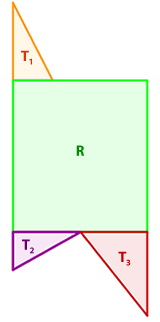 
Recordemos que el área de un triángulo es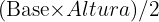 
y el área de una rectángulo es 
.
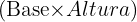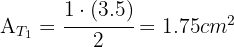
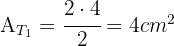
Hallar el área de la siguiente figura.
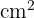
Este campo es obligatorio.
Podemos dividir la figura en un triángulo de base 
y altura , más un romboide de base y altura 
. Así calculamos las áreas del triángulo y del romboide para luego sumarlas y obtener el área total.
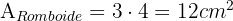. El área de un romboide es .
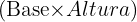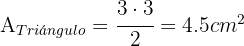. El área de un triángulo es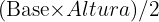
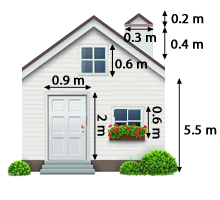
Queremos pintar la parte de la fachada y chimenea de la casa que se observa en la imagen. Sabemos que el área de la fachada incluyendo la puerta y las ventanas es de 55m², y que la chimenea se compone de un rectángulo de 0.4m por 0.3m más un triángulo. Un bote de 1 Kg de pintura cuesta 3 €.
Sabiendo que con 1 Kg de pintura se pintan aproximadamente 8 m² y el bote más pequeño que venden de pintura es el de 1 Kg, ¿cuánto nos costará la pintura necesaria?
Este campo es obligatorio.
En primer lugar calculamos el área de la zona que vamos a pintar.
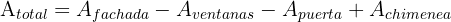
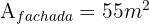
Ya que tenemos dos ventanas cuadradas, entonces
Como la puerta es rectangular, entonces
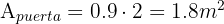
La chimenea se compone de un rectángulo y un triángulo, entonces
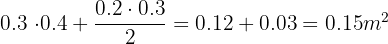
Al realizar la suma y resta de áreas correspondientes tenemos que
Como con 1 Kg de pintura se pintan 8 m², entonces necesitaremos
Como lo mínimo que podemos comprar es 1 Kg nos hacen falta 7 Kg.
Nos costará 
€
Halla el área de un pentágono regular de 8 cm de lado y 5 cm de radio.
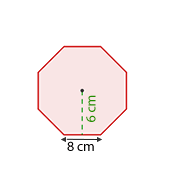
Y el área de un octógono regular de 8 cm de lado y 6 cm de apotema.
Este campo es obligatorio.
Recordemos que el área de un polígono regular es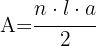 
, donde 
es el número de lados, 
la longitud de un lado y 
es el apotema, el cual se define como el segmento que une el centro del polígono con el punto medio de un lado. En nuestro caso un pentágono es un polígono regular de 
lados y un octógono es un polígono regular de 
lados. Así que utilizaremos la fórmula anterior para calcular sus áreas.
Área del pentágono
Primero debemos hallar la medida del apotema. Esto lo hacemos hayan la altura de un triángulo isosceles de dos lados de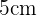 
y uno de 
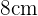. Para hallar la altura utilizamos el teorema de Pitagoras.
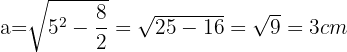
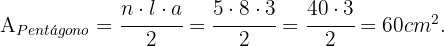
Área del octógono
En el caso del octógono ya nos estan dando el valor del apotema, el cual es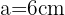 
. Ya que el octógono tiene lados que miden 
, entonces
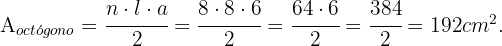
¿Cuál es el área de un dodecágono regular de 5 cm de lado y apotema 9.3 cm?
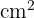
Este campo es obligatorio.
Ya que un dodecágono es un polígono regular de 
lados, hallaremos su área utilizando la siguiente fórmula 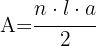, donde es el número de lados, la longitud de un lado y es el apotema, el cual se define como el segmento que une el centro del polígono con el punto medio de un lado. Ya que el apotema vale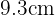 
y un lado mide 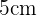, entonces
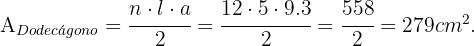
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.