
Elementos notables de un triángulo
Alturas de un triángulo
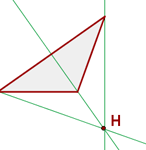
Altura es cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o su prolongación).
Ortocentro
Es el punto de corte de las tres alturas.
Medianas de un triángulo
Mediana es cada una de las rectas que une el punto medio de un lado con el vértice opuesto.
Baricentro
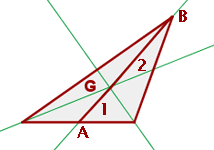
Es el punto de corte de las tres medianas.
El baricentro divide a cada mediana en dos segmentos, el segmento que une el baricentro con el vértice mide el doble que el segmento que une baricentro con el punto medio del lado opuesto.
¿Y si pruebas con un profesor de mates de Superprof?
Mediatrices de un triángulo
Mediatriz es cada una de las rectas perpendiculares trazadas a un lado por su punto medio.
Circuncentro
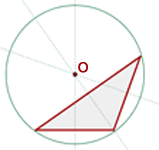
Es el punto de corte de las tres mediatrices.
Es el centro de una circunferencia circunscrita al triángulo.
Bisectrices de un triángulo
Bisectriz es cada una de las rectas que divide a un ángulo en dos ángulos iguales.
Incentro
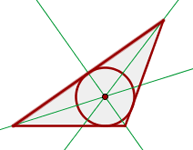
Es el punto de corte de las tres bisetrices.
Es el centro de una circunferencia inscrita en el triángulo.
Recta de Euler
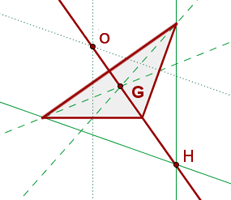
El ortocentro, el baricentro y el circuncentro de un triángulo no equilátero están alineados; es decir, pertenecen a la misma recta, llamada recta de Euler.
Ejercicios propuestos
Para el triángulo con vértices 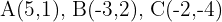 encontrar:
encontrar:
las alturas
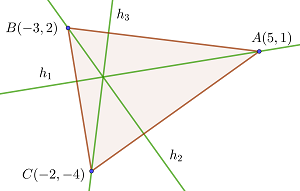
1 Buscamos la ecuación de la altura 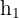 que pasa por el vértice
que pasa por el vértice  y el lado opuesto a este.
y el lado opuesto a este.
Como la altura es perpendicular al lado opuesto, calculamos la pendiente  del lado
del lado 
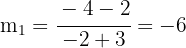
La pendiente 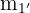 de la altura es
de la altura es
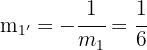
La altura 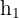 tiene pendiente
tiene pendiente 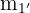 y pasa por el punto
y pasa por el punto  . Calculamos su ecuación
. Calculamos su ecuación
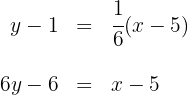
Así, la ecuación de la altura 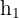 es
es 
2 Buscamos la ecuación de la altura 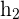 que pasa por el vértice
que pasa por el vértice  y el lado opuesto a este.
y el lado opuesto a este.
Como la altura es perpendicular al lado opuesto, calculamos la pendiente  del lado
del lado 

La pendiente 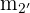 de la altura es
de la altura es
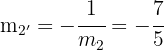
La altura 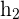 tiene pendiente
tiene pendiente 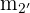 y pasa por el punto
y pasa por el punto  . Calculamos su ecuación
. Calculamos su ecuación
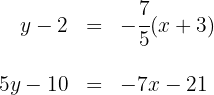
Así, la ecuación de la altura 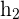 es
es 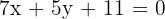
3 Buscamos la ecuación de la altura 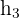 que pasa por el vértice
que pasa por el vértice  y el lado opuesto a este.
y el lado opuesto a este.
Como la altura es perpendicular al lado opuesto, calculamos la pendiente 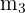 del lado
del lado 

La pendiente 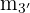 de la altura es
de la altura es
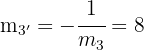
La altura 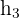 tiene pendiente
tiene pendiente 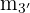 y pasa por el punto
y pasa por el punto  . Calculamos su ecuación
. Calculamos su ecuación
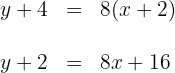
Así, la ecuación de la altura 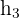 es
es 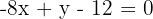
el ortocentro
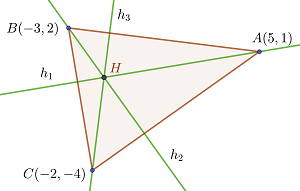
1 Buscamos la intersección de las alturas  para lo cual multiplicamos por 7 la primera altura y sumamos la segunda altura para obtener la segunda coordenada del ortocentro
para lo cual multiplicamos por 7 la primera altura y sumamos la segunda altura para obtener la segunda coordenada del ortocentro

2 Sustituimos el valor de la segunda coordenada del ortocentro en la ecuación de la primera altura y despejamos para obtener la primera coordenada del ortocentro
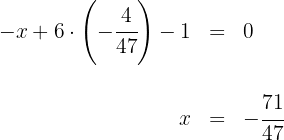
3 Verificamos que el ortocentro pertenece a la altura 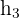

la igualdad se satisface por lo que el ortocentro 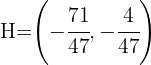 es la intersección de las tres alturas
es la intersección de las tres alturas
las medianas
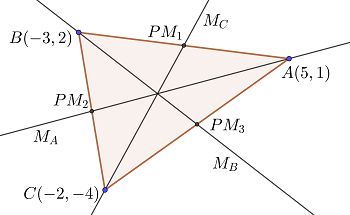
1 Buscamos los puntos medios de los lados del triángulo
El punto medio 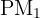 del lado
del lado  es
es
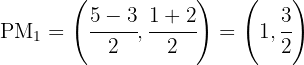
El punto medio  del lado
del lado  es
es

El punto medio 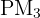 del lado
del lado  es
es

2 Buscamos la ecuación de la mediana 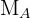 que pasa por el vértice
que pasa por el vértice  y el punto medio del lado opuesto a este
y el punto medio del lado opuesto a este
Calculamos la pendiente que pasa por  y
y 

La mediana 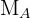 tiene pendiente
tiene pendiente  y pasa por el punto
y pasa por el punto  . Calculamos su ecuación
. Calculamos su ecuación
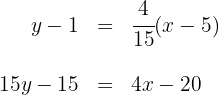
Así, la ecuación de la mediana 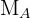 es
es 
3 Buscamos la ecuación de la mediana  que pasa por el vértice
que pasa por el vértice  y el punto medio del lado opuesto a este
y el punto medio del lado opuesto a este
Calculamos la pendiente que pasa por  y
y 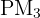
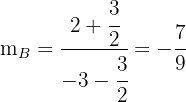
La mediana  tiene pendiente
tiene pendiente 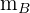 y pasa por el punto
y pasa por el punto  . Calculamos su ecuación
. Calculamos su ecuación
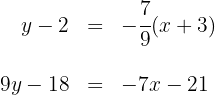
Así, la ecuación de la mediana  es
es 
4 Buscamos la ecuación de la mediana  que pasa por el vértice
que pasa por el vértice  y el punto medio del lado opuesto a este
y el punto medio del lado opuesto a este
Calculamos la pendiente que pasa por  y
y 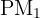

La mediana  tiene pendiente
tiene pendiente 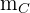 y pasa por el punto
y pasa por el punto  . Calculamos su ecuación
. Calculamos su ecuación
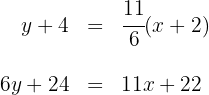
Así, la ecuación de la mediana  es
es 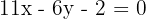
el baricentro
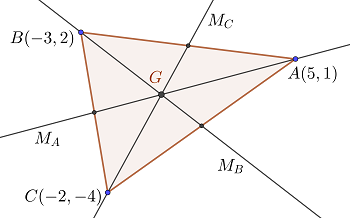
1 Buscamos la intersección de las medianas 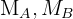 para lo cual multiplicamos por
para lo cual multiplicamos por  la primera mediana, por
la primera mediana, por  la segunda mediana y sumamos ambas medianas para obtener la segunda coordenada del baricentro
la segunda mediana y sumamos ambas medianas para obtener la segunda coordenada del baricentro

2 Sustituimos el valor de la segunda coordenada del baricentro en la ecuación de la segunda mediana y despejamos para obtener la primera coordenada del baricentro
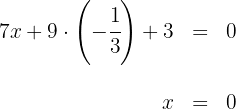
3 Verificamos que el baricentro pertenece a la mediana 
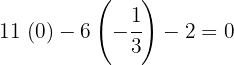
la igualdad se satisface por lo que el baricentro 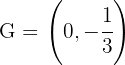 es la intersección de las tres medianas
es la intersección de las tres medianas
las mediatrices
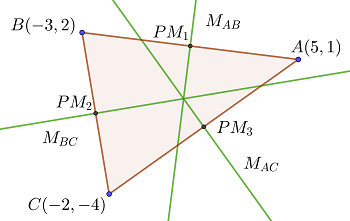
1 Buscamos los puntos medios de los lados del triángulo
El punto medio 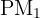 del lado
del lado  es
es
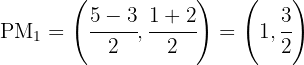
El punto medio  del lado
del lado  es
es

El punto medio 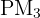 del lado
del lado  es
es

2 Buscamos la ecuación de la mediatriz  que pasa por el punto medio de
que pasa por el punto medio de  y es perpendicular a este.
y es perpendicular a este.
Calculamos la pendiente  del lado
del lado 
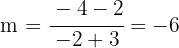
La pendiente 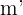 de la mediatriz es
de la mediatriz es

La mediatriz  tiene pendiente
tiene pendiente  y pasa por el punto
y pasa por el punto  . Calculamos su ecuación
. Calculamos su ecuación
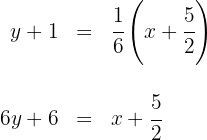
Así, la ecuación de la mediatriz  es
es 
3 Buscamos la ecuación de la mediatriz  que pasa por el punto medio de
que pasa por el punto medio de  y es perpendicular a este.
y es perpendicular a este.
Calculamos la pendiente  del lado
del lado 

La pendiente 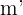 de la mediatriz es
de la mediatriz es
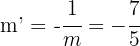
La mediatriz  tiene pendiente
tiene pendiente 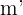 y pasa por el punto
y pasa por el punto 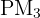 . Calculamos su ecuación
. Calculamos su ecuación
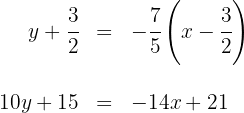
Así, la ecuación de la mediatriz  es
es 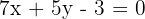
4 Buscamos la ecuación de la mediatriz  que pasa por el punto medio de
que pasa por el punto medio de  y es perpendicular a este.
y es perpendicular a este.
Calculamos la pendiente  del lado
del lado 

La pendiente 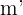 de la mediatriz es
de la mediatriz es

La mediatriz  tiene pendiente
tiene pendiente 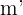 y pasa por el punto
y pasa por el punto 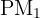 . Calculamos su ecuación
. Calculamos su ecuación

Así, la ecuación de la altura  es
es 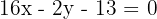
el circuncentro

1 Buscamos la intersección de las mediatrices 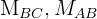 para lo cual multiplicamos por
para lo cual multiplicamos por  la primera mediatriz y sumamos ambas mediatrices para obtener la segunda coordenada del circuncentro
la primera mediatriz y sumamos ambas mediatrices para obtener la segunda coordenada del circuncentro
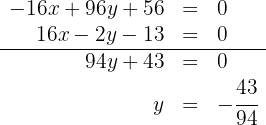
2 Sustituimos el valor de la segunda coordenada del circuncentro en la ecuación de la segunda mediatriz y despejamos para obtener la primera coordenada del circuncentro
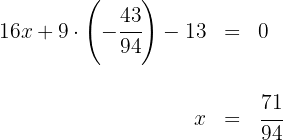
3 Verificamos que el circuncentro pertenece a la mediatriz 
7x + 5y - 3
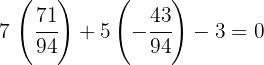
la igualdad se satisface por lo que el circuncentro  es la intersección de las tres mediatrices
es la intersección de las tres mediatrices
las bisectrices
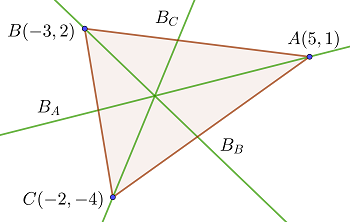
1 Para encontrar la ecuación de una bisectriz, basta igualar la distancia de los puntos de la bisectriz con los lados del ángulo en cuestión, esto es, si los lados que forman el ángulos son
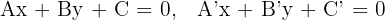
entonces la bisectriz se obtiene de

2 Buscamos la ecuación de la bisectriz de  para esto necesitamos encontrar las ecuaciones de los lados
para esto necesitamos encontrar las ecuaciones de los lados  y
y  . Empleando la ecuación de la recta que pasa por dos puntos obtenemos:
. Empleando la ecuación de la recta que pasa por dos puntos obtenemos:
la recta 

la ecuación es
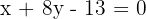
la recta 
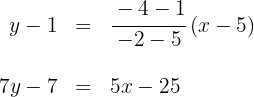
la ecuación es

Aplicamos la fórmula para obtener la bisectriz

Así, la ecuación de la bisectriz 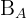 es
es
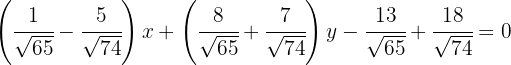
3 Buscamos la ecuación de la bisectriz de  para esto necesitamos encontrar las ecuaciones de los lados
para esto necesitamos encontrar las ecuaciones de los lados  y
y  . Empleando la ecuación de la recta que pasa por dos puntos obtenemos:
. Empleando la ecuación de la recta que pasa por dos puntos obtenemos:
la recta 

la ecuación es
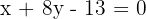
la recta 

la ecuación es
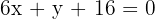
Aplicamos la fórmula para obtener la bisectriz

Así, la ecuación de la bisectriz 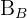 es
es

4 Buscamos la ecuación de la bisectriz de  para esto necesitamos encontrar las ecuaciones de los lados
para esto necesitamos encontrar las ecuaciones de los lados  y
y  . Empleando la ecuación de la recta que pasa por dos puntos obtenemos:
. Empleando la ecuación de la recta que pasa por dos puntos obtenemos:
la recta 
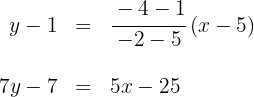
la ecuación es

la recta 

la ecuación es
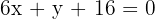
Aplicamos la fórmula para obtener la bisectriz
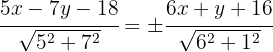
Así, la ecuación de la bisectriz 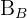 es
es
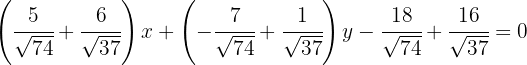
el incentro
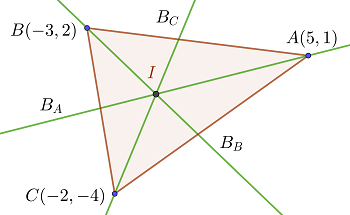
1 Buscamos la intersección de las bisectrices 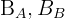 para lo cual multiplicamos por
para lo cual multiplicamos por 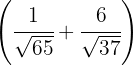 la primera bisectriz, por
la primera bisectriz, por 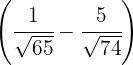 y sumamos ambas bisectrices para obtener la segunda coordenada del incentro
y sumamos ambas bisectrices para obtener la segunda coordenada del incentro

2 Sustituimos el valor de la segunda coordenada del incentro en la ecuación de la primera bisectriz y despejamos para obtener la primera coordenada del incentro

la recta de Euler
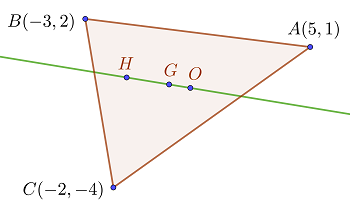
1 Buscamos la recta que pasa por el ortocentro 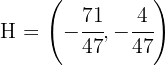 , el baricentro
, el baricentro 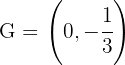 y el circuncentro
y el circuncentro 
2Calculamos la pendiente  para el ortocentro y el baricentro
para el ortocentro y el baricentro
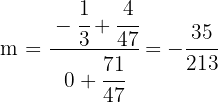
La recta de Euler tiene pendiente  y pasa por el punto
y pasa por el punto 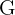 . Calculamos su ecuación
. Calculamos su ecuación

Así, la ecuación de la recta de Euler es 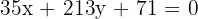
Verifica que el incentro no pertenece a la recta de Euler

1 Basta sustituir el incentro 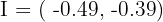 en la ecuación de la recta de Euler y verificar que no la satisface]
en la ecuación de la recta de Euler y verificar que no la satisface]
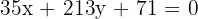
Sustituimos

Como el incentro no satisface la ecuación de la recta de Euler, entonces concluimos que el incentro no se encuentra sobre la recta de Euler.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.