El Teorema de Thales es un concepto fundamental en la geometría que nos ayuda a comprender las propiedades de las figuras geométricas y las relaciones entre sus elementos. Este teorema establece una poderosa conexión entre las líneas paralelas y los triángulos semejantes, y su aplicación se extiende a una amplia variedad de problemas geométricos.
En los siguientes ejercicios, exploraremos cómo aplicar el Teorema de Thales para resolver problemas prácticos y demostrar sus propiedades en situaciones del mundo real. A través de estos ejercicios, desarrollaremos una comprensión más profunda de este importante teorema y su relevancia en la resolución de problemas geométricos cotidianos.
¡Vamos a comenzar a explorar el fascinante mundo de Thales!
Resuelve los siguientes ejercicios del teorema de Thales eligiendo la respuesta correcta:
Para poder aplicar el teorema de Thales necesitamos...
Selecciona una respuesta.
Una de las aplicaciones del teorema de Thales es...
Selecciona una respuesta.
Podemos aplicar el teorema de Thales en triángulos cuando...
Selecciona una respuesta.
El teorema de Thales dice que si varias rectas paralelas son cortadas por dos secantes, los segmentos correspondientes determinados por las secantes son...
Selecciona una respuesta.
Dos triángulos satisfacen Thales cuando...
Selecciona una respuesta.
Si dos triángulos tienen sus lados paralelos, entonces por el teorema de Thales los dos triángulos son...
Selecciona una respuesta.
Por el teorema de Thales, dos triángulos rectángulos son semejantes cuando...
Selecciona una respuesta.
Sabiendo que las rectas  ,
, 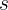 y
y  son paralelas, la longitud de
son paralelas, la longitud de  es
es

Selecciona una respuesta.
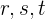 son paralelas, estamos en las condiciones del teorema de Thales, por lo que podemos aplicarlo:
son paralelas, estamos en las condiciones del teorema de Thales, por lo que podemos aplicarlo: 
Sabiendo que las rectas  ,
, 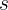 y
y  son paralelas, las longitudes que faltan son:
son paralelas, las longitudes que faltan son:

Selecciona una respuesta.
Como 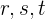 son paralelas, estamos en las condiciones del teorema de Thales, por lo que podemos aplicarlo:
son paralelas, estamos en las condiciones del teorema de Thales, por lo que podemos aplicarlo: 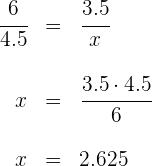
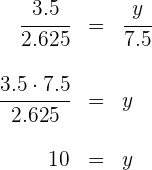
Sean  y
y 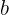 dos rectas cualesquiera y
dos rectas cualesquiera y  y
y 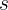 dos rectas que las cortan. Si los segmentos que determinan
dos rectas que las cortan. Si los segmentos que determinan  y
y 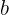 son
son  ,
, 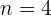 ,
,  y
y 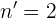 entonces...
entonces...
Selecciona una respuesta.
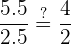
 No se verifica el teorema de Thales, por lo que las rectas
No se verifica el teorema de Thales, por lo que las rectas  y
y 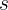 no son paralelas.
no son paralelas.Sean  y
y 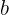 dos rectas cualesquiera y
dos rectas cualesquiera y  y
y 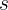 dos rectas que las cortan. Si los segmentos que determinan
dos rectas que las cortan. Si los segmentos que determinan  y
y 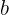 son
son 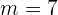 ,
,  ,
, 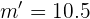 y
y  entonces...
entonces...
Selecciona una respuesta.
Comprobamos si se cumple el teorema de Thales: 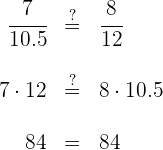 Se verifica el teorema de Thales, por lo que las rectas
Se verifica el teorema de Thales, por lo que las rectas  y
y 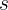 son paralelas.
son paralelas.
Sabiendo que el segmento 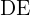 es paralelo a la base del triángulo, las medidas de los segmentos
es paralelo a la base del triángulo, las medidas de los segmentos  y
y 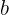 son...
son...
Selecciona una respuesta.
En primer lugar,  , basta hacer
, basta hacer 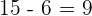 .
.
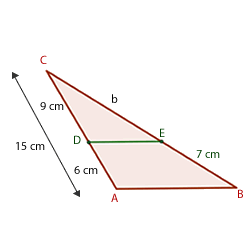
A continuación aplicamos el teorema de Thales:

Sabiendo que los segmentos que miden 3 cm y 4 cm son paralelos, calcular  y
y 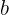 .
.
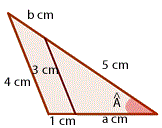
Selecciona una respuesta.
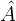 y los lados que miden 3 y 4 cm son paralelos. Aplicamos el teorema de Thales:
y los lados que miden 3 y 4 cm son paralelos. Aplicamos el teorema de Thales: 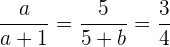 Desarrollamos la ecuación conformada por la primera y última parte, y despejamos
Desarrollamos la ecuación conformada por la primera y última parte, y despejamos 
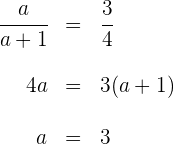 De la última igualdad despejamos
De la última igualdad despejamos 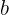
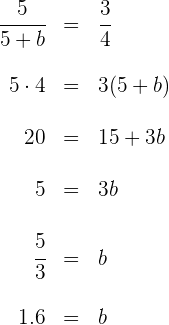
Si llamamos  a la altura de los libros aplicando el teorema de Thales,
a la altura de los libros aplicando el teorema de Thales,

cm
Este campo es obligatorio.
 a la altura de los libros y aplicamos Thales
a la altura de los libros y aplicamos Thales 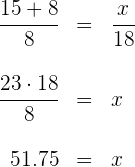
Observando la escalera que aparece en el dibujo calcula la longitud de la cuerda que une los peldaños de la escalera con su parte posterior.
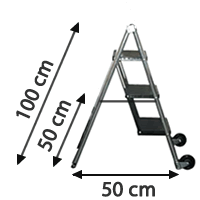
cm
Este campo es obligatorio.
 a la longitud de la cuerda y aplicamos Thales
a la longitud de la cuerda y aplicamos Thales 
Si tienes dudas puedes consultar la teoría
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.