Capítulos
¿Conoces nuestras clases de matematicas en A Coruña?

Elementos de un polígono
1 Lados: son los segmentos que lo limitan.
2 Vértices: son los puntos donde concurren dos lados.
3 Ángulos interiores de un polígono: son los determinados por dos lados consecutivos.
4Diagonal: son los segmentos que determinan dos vértices no consecutivos
Número de diagonales de un polígono
Si  es el número de lados de un polígono:
es el número de lados de un polígono:
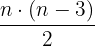
Polígonos regulares
Un polígono regular es el que tiene sus ángulos iguales y sus lados iguales.
Elementos de un polígono regular
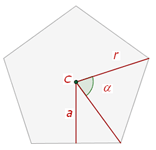
1 Centro: punto interior que equidista de cada vértice.
2 Radio: es el segmento que va del centro a cada vértice.
3 Apotema: distancia del centro al punto medio de un lado.
4 Ángulos: formados por dos radios consecutivos
Ejemplo:
Si  es el número de lados de un polígono:
es el número de lados de un polígono:
Ángulo central 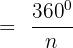
Ángulo interior 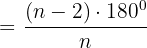
Polígono inscrito
Un polígono está inscrito en una circunferencia si todos sus vértices están contenidos en ella.
1 Circunferencia circunscrita
Es la que toca a cada vértice del polígono.
Su centro equidista de todos los vértices.
Su radio es el radio del polígono.
2 Circunferencia inscrita
Es la que toca al polígono en el punto medio de cada lado.
Su centro equidista de todos los lados.
Su radio es la apotema del polígono.
Triángulos
Un triángulo es un polígono con tres lados.
Propiedades de los triángulos
1 Un lado de un triángulo es menor que la suma de los otros dos y mayor que su diferencia.
2 La suma de los ángulos interiores de un triángulo es igual a 180°.
3 El valor de un ángulo exterior es igual a la suma de los dos interiores no adyacentes.
Clasificación de los triángulos según sus lados
1 Triángulo equilátero - Tres lados iguales.

2 Triángulo isósceles - Dos lados iguales.

3 Triángulo escaleno - Tres lados desiguales.

¿Y si pruebas nuestras clases de matematicas en Madrid?
Clasificación de los triángulos según sus ángulos
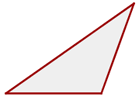
1 Triángulo acutángulo - Tres ángulos agudos
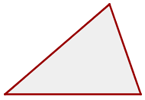
2 Triángulo rectángulo - Un ángulo recto. El lado mayor es la hipotenusa. Los lados menores son los catetos.
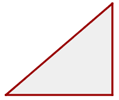
3 Triángulo obtusángulo - Un ángulo obtuso.
Elementos de un triángulo
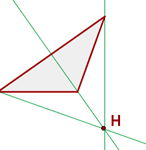
1 La altura es cada una de las rectas perpendiculares trazadas desde un vértice al lado opuesto (o su prolongación).
2 El ortocentro es el punto de corte de las tres alturas.
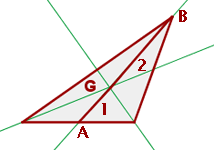
3 La mediana es cada una de las rectas que une el punto medio de un lado con el vértice opuesto.
4 El baricentro es el punto de corte de las tres medianas. El baricentro divide a cada mediana en dos segmentos.
El segmento que une el baricentro con el vértice mide el doble que el segmento que une baricentro con el punto medio del lado opuesto.
5 La mediatriz es cada una de las rectas perpendiculares trazadas a un lado por su punto medio.
6 El circuncentro es el punto de corte de las tres mediatrices. Es el centro de una circunferencia circunscrita al triángulo.
7 La bisectriz es cada una de las rectas que divide a un ángulo en dos ángulos iguales.
8 El incentro es el punto de corte de las tres bisectrices. Es el centro de una circunferencia inscrita en el triángulo.
Recta de Euler
El ortocentro, el baricentro y el circuncentro de un triángulo no equilátero están alineados; es decir, pertenecen a la misma recta, llamada recta de Euler.
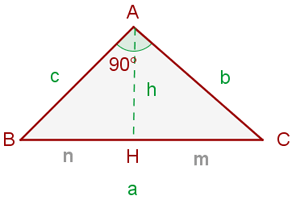
Teorema del cateto
En todo triángulo rectángulo un cateto es media proporcional entre la hipotenusa y su proyección sobre ella.
Teorema de la altura
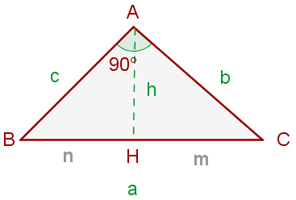
En un triángulo rectángulo, la altura relativa a la hipotenusa es media proporcional entre los 2 segmentos que dividen a ésta.
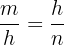
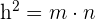
Teorema de Pitágoras
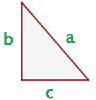
En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

Para conocer el valor de los catetos o el de la hipotenusa despejamos y las formulas quedan así:
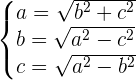
El círculo
El círculo es la figura plana comprendida en el interior de una circunferencia.

Elementos de un círculo
Segmento circular - Porción de círculo limitada por una cuerda y el arco correspondiente.

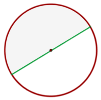
Semicírculo - Porción del círculo limitada por un diámetro y el arco correspondiente. Equivale a la mitad del círculo.
Zona circular - Porción de círculo limitada por dos cuerdas.

Sector circular - Porción de círculo limitada por dos radios.
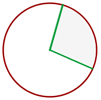
Corona circular - Porción de círculo limitada por dos círculos concéntricos.

Trapecio circular - Porción de círculo limitada por dos radios y una corona circular.

Fórmulas de áreas y segmentos del círculo
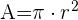
Ejemplo:
La longitud de una circunferencia es 43.96 cm. ¿Cuál es el área del círculo?
Tenemos que 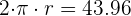 y despejamos
y despejamos 
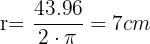
Ahora sustituimos en la fórmula del área del circulo
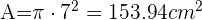
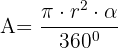
Ejemplo
Hallar el área del sector circular cuya cuerda es el lado del cuadrado inscrito, siendo 4 cm el radio de la circunferencia.
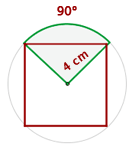
Tenemos  y
y  , entonces aplicamos la fórmula
, entonces aplicamos la fórmula
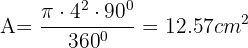
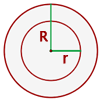
Es igual al área del círculo mayor menos el área del círculo menor.
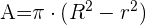
Ejemplo:
En un parque de forma circular de 700 m de radio hay situada en el centro una fuente, también de forma circular, de 5 m de radio. Calcula el área de la zona de paseo.

Tenemos  y
y 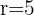 , aplicamos la fórmula
, aplicamos la fórmula

Área de un trapecio circular
Es igual al área del sector circular mayor menos el área del sector circular menor.

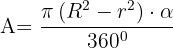
Ejemplo:
Dadas dos circunferencias concéntricas de radio 8 y 5 cm, respectivamente, se trazan los radios OA y OB, que forman un ángulo de 60°. Calcular el área del trapecio circular formado.

Tenemos 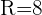 ,
, 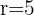 y
y 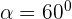 , ahora aplicamos la fórmula
, ahora aplicamos la fórmula
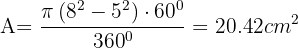
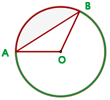
Área del segmento circular AB = Área del sector circular AOB − Área del triángulo AOB
Ejemplo:
Sobre un círculo de 4 cm se traza un ángulo central de 60°. Calcular el área del segmento circular comprendido entre la cuerda que une los extremos de los dos radios y su arco correspondiente
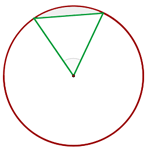
Primero calculamos el área del sector circular con la fórmula
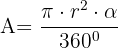
donde  y
y 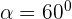 , sustituimos
, sustituimos
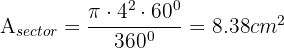
Ahora calculamos el área del triángulo el cual es equilátero, por lo tanto primero calculamos la altura, si trazamos una altura obtenemos dos triángulos rectángulos y podemos aplicar teorema de Pitágoras quedando
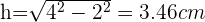
Entonces el área del triangulo es
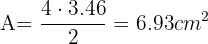
Finalmente el área del segmento circular es
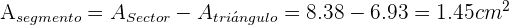
La circunferencia
La circunferencia es una línea curva cerrada cuyos puntos están todos a la misma distancia de un punto fijo llamado centro.

El centro de la circunferencia es el punto del que equidistan todos los puntos de la circunferencia.
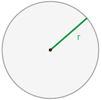
El radio de la circunferencia es el segmento que une el centro de la circunferencia con un punto cualquiera de la misma.
Elementos de la circunferencia
Cuerda - Segmento que une dos puntos de la circunferencia.

Diámetro - Cuerda que pasa por el centro.

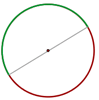
Arco - Cada una de las partes en que una cuerda divide a la circunferencia. Se suele asociar a cada cuerda el menor arco que delimita.

Semicircunferencia - Cada uno de los arcos iguales que abarca un diámetro.
Ángulos en la circunferencia
1 Ángulo central
El ángulo central tiene su vértice en el centro de la circunferencia y sus lados son dos radios.
La medida de un arco es la de su ángulo central correspondiente.


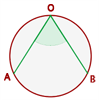
El ángulo inscrito tiene su vértice está en la circunferencia y sus lados son secantes a ella.
Mide la mitad del arco que abarca.
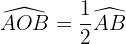
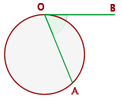
3 Ángulo semi-inscrito
El vértice de ángulo semiinscrito está en la circunferencia, un lado secante y el otro tangente a ella.
Mide la mitad del arco que abarca.
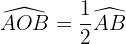
4 Ángulo interior
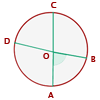
Su vértice es interior a la circunferencia y sus lados secantes a ella.
Mide la mitad de la suma de las medidas de los arcos que abarcan sus lados y las prolongaciones de sus lados.
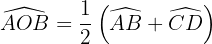
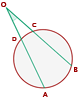
5 Ángulo exterior
Su vértice es un punto exterior a la circunferencia y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella:
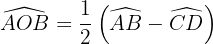


Área y longitud de la circunferencia
Longitud de una circunferencia

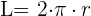
Ejemplo:
Calcular la longitud de una rueda de 180 cm de diámetro.
L = 2 · π · r
r= 1/2 · D = 180:2=90
L= 2 · π · 90 = 565.47 cm
Tenemos la fórmula
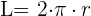
También tenemos 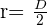 donde
donde  es el diámetro, por lo tanto
es el diámetro, por lo tanto

Ahora con el valor del radio aplicamos la fórmula
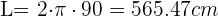

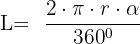
Ejemplo:
Los brazos de un columpio miden 1.8 m de largo y pueden describir como máximo un ángulo de 146°. Calcula el espacio recorrido por el asiento del columpio cuando el ángulo descrito en su balanceo es el máximo.
Tenemos 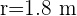 y
y  y aplicamos la fórmula de Longitud de un arco de circunferencia
y aplicamos la fórmula de Longitud de un arco de circunferencia
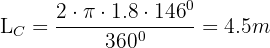
Polígonos estrellados
Un polígono regular estrellado se construye uniendo los vértices no consecutivos, de un polígono regular convexo, de forma continua.
Se denotan por N/M, siendo N el número de vértices del polígono regular convexo y M el salto entre vértices.
N/M ha de ser fracción irreducible.
El polígono N/M es el mismo que el N/(N-M), ya que el polígono estrellado que se obtiene uniendo vértices en un sentido y en el contrario es el mismo.
Perímetro de un polígono: Es la suma de las longitudes de los lados de un polígono.
Área: Es la medida de la región o superficie encerrada por una figura plana
1 Área de un cuadrado:

Diagonal

Perímetro
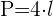
Área
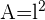
2 Área de un rectángulo:



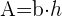
3 Área de un rombo:
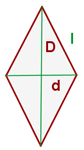
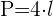
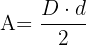
4 Área de un romboide:
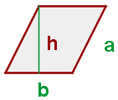
Perímetro
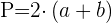
Área
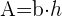
5 Área de un trapecio:

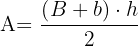
6 Área de un triángulo:
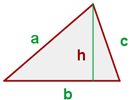
Perímetro

Área
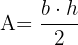
7 Área de un polígono:

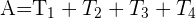
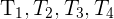 son las áreas de los triángulos.
son las áreas de los triángulos.El área se obtiene triangulando el polígono y sumando el área de dichos triángulos.
Ejemplo:
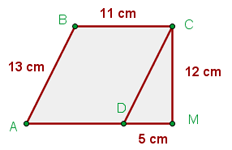
Calcular el área del siguiente polígono:
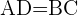 ;
; 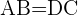 entonces es un romboide y para calcular el área usaremos la expresión:
entonces es un romboide y para calcular el área usaremos la expresión: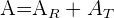
Donde
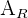 es el área del rectángulo y
es el área del rectángulo y 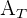 es el área del triángulo.
es el área del triángulo.Entonces si la altura es
 , la base del rectángulo es
, la base del rectángulo es  y la base del triángulo es
y la base del triángulo es  aplicamos las formulas
aplicamos las formulas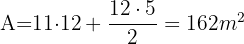
8 Área de un polígono regular:
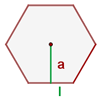

Área
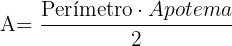
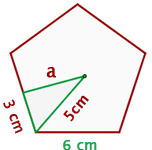
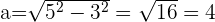
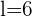 y como es un pentágono entonces el perímetro es
y como es un pentágono entonces el perímetro es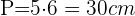
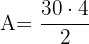


Según podemos ver de la figura, tenemos que encontrar el apotema usando teorema de Pitágoras

Ya que
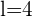 y como es un hexágono entonces el perímetro es
y como es un hexágono entonces el perímetro es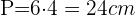
Por lo tanto el área seria
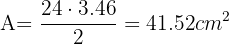
¿Y si pruebas nuestras clases de matematicas en Granada?
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.