Capítulos
¡Bienvenidos a nuestra sección de Ejercicios sobre la Circunferencia y el Círculo!
En esta serie de ejercicios, exploraremos las propiedades y conceptos fundamentales relacionados con la circunferencia y el círculo, dos elementos clave en la geometría. Estas figuras geométricas no solo son esenciales en sí mismas, sino que también tienen aplicaciones prácticas en diversos campos, desde la física hasta la ingeniería y más allá.
A través de estos ejercicios, te sumergirás en la comprensión de temas como el cálculo del perímetro y área de un círculo, la relación entre la circunferencia y el diámetro, el uso de fórmulas fundamentales y la resolución de problemas prácticos que involucran circunferencias y círculos.

Cálculo de distancia
1La rueda de un camión tiene  cm de radio. ¿Cuánto ha recorrido el camión cuando la rueda ha dado
cm de radio. ¿Cuánto ha recorrido el camión cuando la rueda ha dado  vueltas?
vueltas?
 entonces su diámetro es
entonces su diámetro es 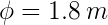 .Por otro lado, recordemos que el perímetro representa la longitud de la circunferencia, y esto equivale a lo que el camión recorre al dar una vuelta. Considerando esto tenemos que el perímetro de la rueda es
.Por otro lado, recordemos que el perímetro representa la longitud de la circunferencia, y esto equivale a lo que el camión recorre al dar una vuelta. Considerando esto tenemos que el perímetro de la rueda es 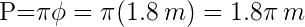 .Finalmente, dado que nos interesa saber la distancia recorrida del camión durante 100 vueltas, entonces:
.Finalmente, dado que nos interesa saber la distancia recorrida del camión durante 100 vueltas, entonces: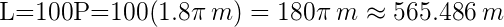 .
.2Un faro barre con su luz un ángulo plano de 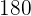 . Si el alcance máximo del faro es de
. Si el alcance máximo del faro es de  millas, ¿cuál es la longitud máxima en metros del arco correspondiente?
millas, ¿cuál es la longitud máxima en metros del arco correspondiente?
 de una circunferencia de radio
de una circunferencia de radio  subtiende un ángulo central de
subtiende un ángulo central de  radianes, entonces
radianes, entonces 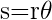 . Esta fórmula es la que se utilizará para resolver el problema planteado, sin embargo necesitamos el ángulo en radianes, es decir
. Esta fórmula es la que se utilizará para resolver el problema planteado, sin embargo necesitamos el ángulo en radianes, es decir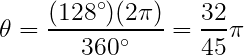 Luego, la longitud de arco es
Luego, la longitud de arco es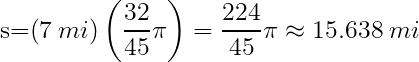 En este problema consideremos que
En este problema consideremos que 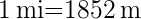 ya que esta es la unidad de longitud utilizada en navegación marítima y aérea. Por lo tanto la longitud en metros del arco es:
ya que esta es la unidad de longitud utilizada en navegación marítima y aérea. Por lo tanto la longitud en metros del arco es:
Cálculo de área
3La longitud de una circunferencia es  cm. ¿Cuál es el área del círculo?
cm. ¿Cuál es el área del círculo?
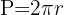 ,donde
,donde  representa el radio del círculo. Podemos reescribir la expresiónde la manera siguiente:
representa el radio del círculo. Podemos reescribir la expresiónde la manera siguiente: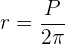
El área del círculo se calcula con la fórmula:

Si sustituyimos el valor de  obtenido previamente obtenemos:
obtenido previamente obtenemos:
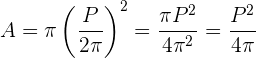
Finalmente considerando el valor numérico de  , el área del círculo es:
, el área del círculo es:

4El área de un sector circular de  es
es 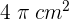 . Calcular el radio del círculo al que pertenece y la longitud de la circunferencia.
. Calcular el radio del círculo al que pertenece y la longitud de la circunferencia.
 donde
donde  representa el número de grados
representa el número de grados es el radio asociado del sector circular.
es el radio asociado del sector circular. De esta expresión tenemos:
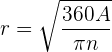
Luego, sustituyendo los valores numéricos del problema, tenemos que el radio del círculo al que pertenece el sector circular es

Finalmente, la longitud de la circunferencia (perímetro) es
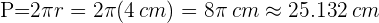
5Hallar el área de un sector circular cuya cuerda es el lado del triángulo equilátero inscrito, siendo  cm el radio de la circunferencia.
cm el radio de la circunferencia.
 ,donde
,donde  es el número de grados
es el número de grados es el radio asociado del sector circular.
es el radio asociado del sector circular. Dado que los ángulos internos de un triángulo equilátero miden todos  , y considerando que el vértice del ángulo central del arco coincide con el centro de la circunferencia (ver figura), este ángulo mide
, y considerando que el vértice del ángulo central del arco coincide con el centro de la circunferencia (ver figura), este ángulo mide

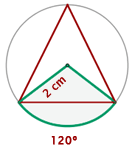
El área del sector circular es:
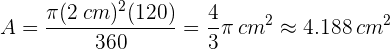
6Dadas dos circunferencias concéntricas de radio  y
y 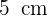 respectivamente, se trazan los radios
respectivamente, se trazan los radios 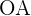 y
y  , que forman un ángulo de
, que forman un ángulo de 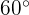 . Calcular el área del trapecio circular formado.
. Calcular el área del trapecio circular formado.
 donde
donde 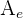 representa el área del sector circular de la circunferencia externa (cuyo radio es
representa el área del sector circular de la circunferencia externa (cuyo radio es 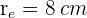 ), mientras que
), mientras que representa el área del sector circular de la circunferencia interna (cuyo radio es
representa el área del sector circular de la circunferencia interna (cuyo radio es  ). Por lo tanto
). Por lo tanto 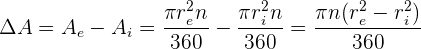
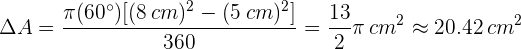
7En un parque de forma circular de 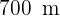 de radio hay situada en el centro una fuente, también de forma circular, de
de radio hay situada en el centro una fuente, también de forma circular, de 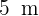 de radio. Calcula el área de la zona de paseo.
de radio. Calcula el área de la zona de paseo.

donde 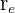 es el radio mayor (radio externo)
es el radio mayor (radio externo)
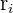 es el radio menor (radio interno).
es el radio menor (radio interno).
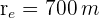
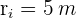
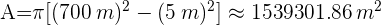
8La superficie de una mesa está formada por una parte central cuadrada de 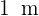 de lado y dos semicírculos adosados en dos lados opuestos. Calcula el área.
de lado y dos semicírculos adosados en dos lados opuestos. Calcula el área.
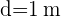 (ver figura).
(ver figura).

 es la longitud de la mesa
es la longitud de la mesa es el diámetro del círculo.
es el diámetro del círculo.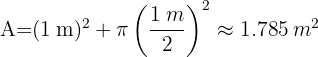
9Calcula el área de la parte sombreada, si el radio del círculo mayor mide 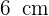 y el radio de los círculos pequeños miden
y el radio de los círculos pequeños miden 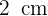 .
.
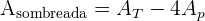
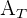 es el área del círculo mayor de radio
es el área del círculo mayor de radio 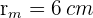
 es el área de cada uno de los círculos pequeños de radio
es el área de cada uno de los círculos pequeños de radio 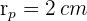
Por lo tanto, tenemos que
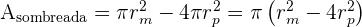 .
.
Finalmente sustituyendo los valores numéricos, se tiene que el área de la parte sombreada es:
10Calcula el área de la parte sombreada, siendo  ,
,  un cuadrado y
un cuadrado y 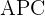 y
y 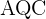 arcos de circunferencia de centros
arcos de circunferencia de centros  y
y  .
.


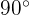 . Por lo tanto,
. Por lo tanto, 
Finalmente sustituyendo datos numéricos en la expresión anterior, el área de 1 segmento circular es
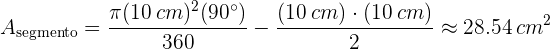
y el área sombreada buscada entonces es
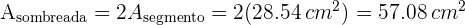
11Un satélite de comunicaciones orbita la Tierra en un ángulo de 45° respecto al ecuador. Si la altura del satélite es de 10,000 kilómetros, ¿cuál es la longitud máxima en kilómetros de la trayectoria que cubre en su órbita?
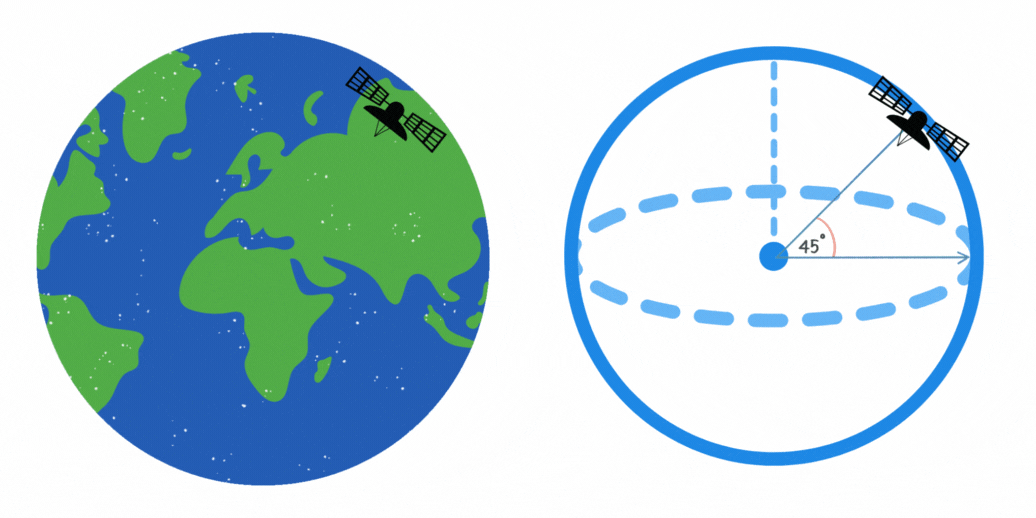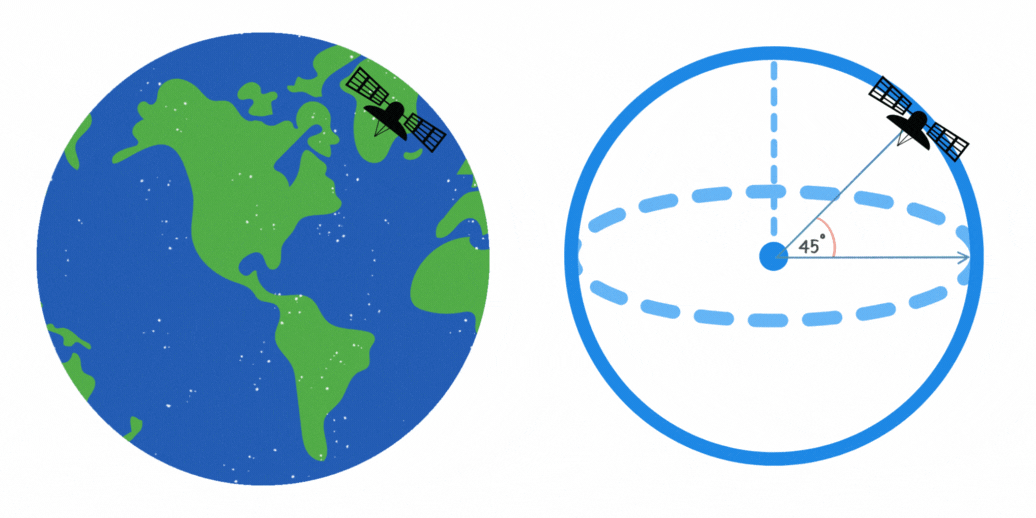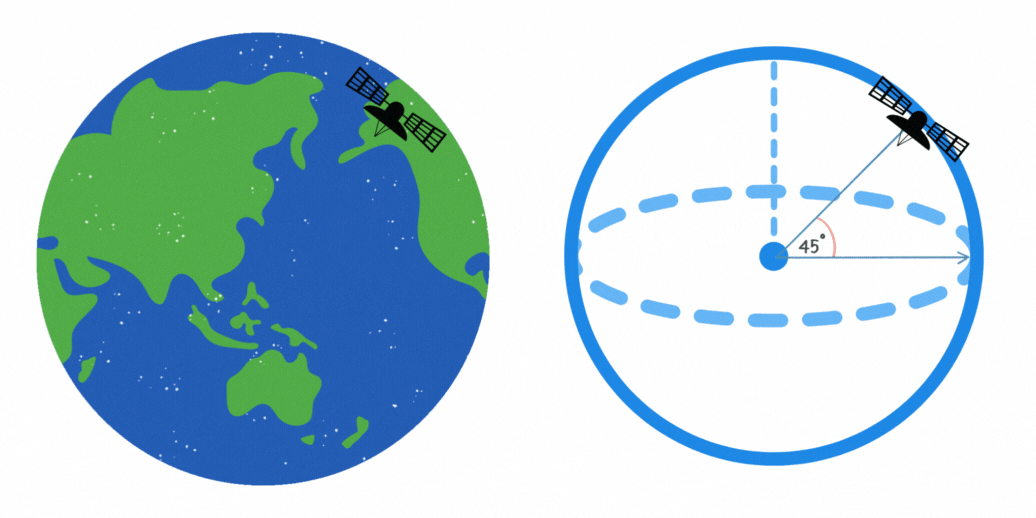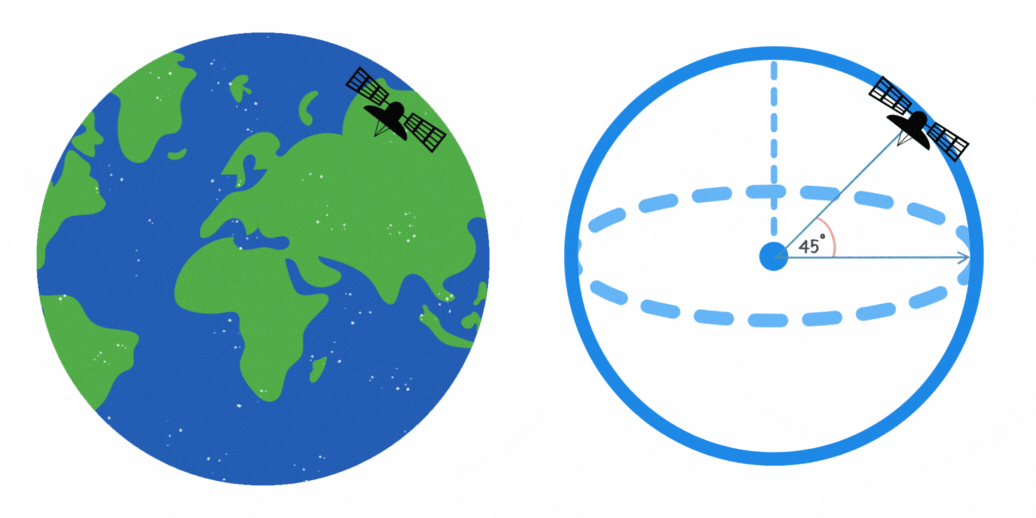
La longitud de la trayectoria del satélite en su órbita se puede calcular con la fórmula del arco de un círculo. Esto se puede apreciar en la figura, ya que el satélite recorre un camino circular de radio constante. La fórmula es
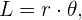
donde 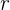 es la distancia del centro de la tierra hasta el satélite,
es la distancia del centro de la tierra hasta el satélite,  es el ángulo en radianes. Recordemos que 45° es equivalente a
es el ángulo en radianes. Recordemos que 45° es equivalente a 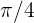 radianes. Por lo tanto, el satélite recorre
radianes. Por lo tanto, el satélite recorre
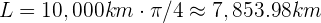
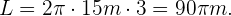
13Una bicicleta con ruedas de 26 cm de diámetro recorre 5 km. ¿Cuántas vueltas completas ha dado cada rueda durante este recorrido?
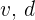 son las vueltas recorridas y el diámetro, respectivamente, la distancia total recorrida se puede calcular mediante
son las vueltas recorridas y el diámetro, respectivamente, la distancia total recorrida se puede calcular mediante 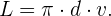
Como concemos la distancia total recorrida, debemos despejar para 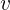 :
:

14 Un pastel circular se corta en 8 porciones iguales. Si el pastel tiene un radio de 20 centímetros, ¿cuánto mide el arco de cada porción? ¿Cuánta área tiene la parte superior del pastel?
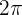 en 8 partes. Por lo que cada rebanada es
en 8 partes. Por lo que cada rebanada es 
del sector completo. Como tiene un radio de 20 cm, tenemos que el área de este sector es de
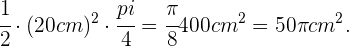
15 ¿Qué radio debe tener una rueda para darle una vuelta completa por el ecuador a la Tierra en 3 revolución?

en 3 revoluciones. Es decir, queremos que el radio 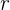 de nuestra rueda sea tal que
de nuestra rueda sea tal que  . Entonces,
. Entonces,
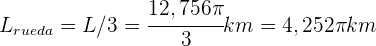
debe ser lo que mide la circunferencia. Por lo que el radio debe ser
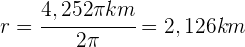
¿Necesitas apoyo adicional? En Superprof te ayudamos a encontrar un curso de matematicas adaptado a tus necesidades.
Cálculo de distancia
La rueda de un camión tiene  cm de radio. ¿Cuánto ha recorrido el camión cuando la rueda ha dado
cm de radio. ¿Cuánto ha recorrido el camión cuando la rueda ha dado  vueltas?
vueltas?
Dado que el radio de la rueda es  entonces su diámetro es
entonces su diámetro es 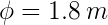 .Por otro lado, recordemos que el perímetro representa la longitud de la circunferencia, y esto equivale a lo que el camión recorre al dar una vuelta. Considerando esto tenemos que el perímetro de la rueda es
.Por otro lado, recordemos que el perímetro representa la longitud de la circunferencia, y esto equivale a lo que el camión recorre al dar una vuelta. Considerando esto tenemos que el perímetro de la rueda es 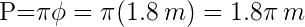 .Finalmente, dado que nos interesa saber la distancia recorrida del camión durante 100 vueltas, entonces:
.Finalmente, dado que nos interesa saber la distancia recorrida del camión durante 100 vueltas, entonces: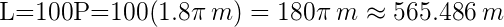 .
.
Un faro barre con su luz un ángulo plano de 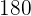 . Si el alcance máximo del faro es de
. Si el alcance máximo del faro es de  millas, ¿cuál es la longitud máxima en metros del arco correspondiente?
millas, ¿cuál es la longitud máxima en metros del arco correspondiente?
Recordemos que si un arco de longitud  de una circunferencia de radio
de una circunferencia de radio  subtiende un ángulo central de
subtiende un ángulo central de  radianes, entonces
radianes, entonces 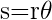 . Esta fórmula es la que se utilizará para resolver el problema planteado, sin embargo necesitamos el ángulo en radianes, es decir
. Esta fórmula es la que se utilizará para resolver el problema planteado, sin embargo necesitamos el ángulo en radianes, es decir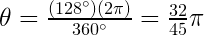 Luego, la longitud de arco es
Luego, la longitud de arco es En este problema consideremos que
En este problema consideremos que 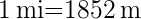 ya que esta es la unidad de longitud utilizada en navegación marítima y aérea. Por lo tanto la longitud en metros del arco es:
ya que esta es la unidad de longitud utilizada en navegación marítima y aérea. Por lo tanto la longitud en metros del arco es:
Cálculo de área
La longitud de una circunferencia es  cm. ¿Cuál es el área del círculo?
cm. ¿Cuál es el área del círculo?
La longitud de la circunferencia representa el perímetro de la misma, el cual se calcula con la fórmula siguiente: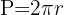 ,donde
,donde  representa el radio del círculo. Podemos reescribir la expresiónde la manera siguiente:
representa el radio del círculo. Podemos reescribir la expresiónde la manera siguiente: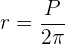 El área del círculo se calcula con la fórmula:
El área del círculo se calcula con la fórmula:

Si sustituyimos el valor de  obtenido previamente obtenemos:
obtenido previamente obtenemos:
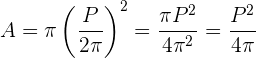
Finalmente considerando el valor numérico de  , el área del círculo es:
, el área del círculo es:

El área de un sector circular de  es
es 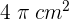 . Calcular el radio del círculo al que pertenece y la longitud de la circunferencia.
. Calcular el radio del círculo al que pertenece y la longitud de la circunferencia.
La fórmula para calcular el área de un sector circular es donde
donde  representa el número de grados
representa el número de grados es el radio asociado del sector circular.De esta expresión tenemos:
es el radio asociado del sector circular.De esta expresión tenemos:
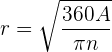
Luego, sustituyendo los valores numéricos del problema, tenemos que el radio del círculo al que pertenece el sector circular es

Finalmente, la longitud de la circunferencia (perímetro) es
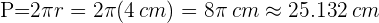
Hallar el área de un sector circular cuya cuerda es el lado del triángulo equilátero inscrito, siendo  cm el radio de la circunferencia.
cm el radio de la circunferencia.
La fórmula para calcular el área de un sector circular es: ,donde
,donde  es el número de grados
es el número de grados es el radio asociado del sector circular.Dado que los ángulos internos de un triángulo equilátero miden todos
es el radio asociado del sector circular.Dado que los ángulos internos de un triángulo equilátero miden todos  , y considerando que el vértice del ángulo central del arco coincide con el centro de la circunferencia (ver figura), este ángulo mide
, y considerando que el vértice del ángulo central del arco coincide con el centro de la circunferencia (ver figura), este ángulo mide


El área del sector circular es:
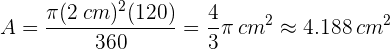
Dadas dos circunferencias concéntricas de radio  y
y 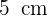 respectivamente, se trazan los radios
respectivamente, se trazan los radios 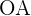 y
y  , que forman un ángulo de
, que forman un ángulo de 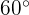 . Calcular el área del trapecio circular formado.
. Calcular el área del trapecio circular formado.
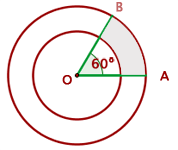
El área del trapecio circular formado (ver figura) se puede calcular así: donde
donde 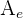 representa el área del sector circular de la circunferencia externa (cuyo radio es
representa el área del sector circular de la circunferencia externa (cuyo radio es 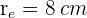 ), mientras que
), mientras que representa el área del sector circular de la circunferencia interna (cuyo radio es
representa el área del sector circular de la circunferencia interna (cuyo radio es  ). Por lo tanto
). Por lo tanto
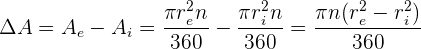
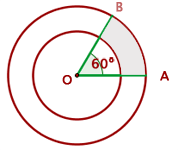
Luego, sustituymos los valores numéricos en la fórmula y obtenemos el área: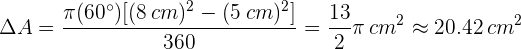
En un parque de forma circular de 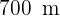 de radio hay situada en el centro una fuente, también de forma circular, de
de radio hay situada en el centro una fuente, también de forma circular, de 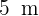 de radio. Calcula el área de la zona de paseo.
de radio. Calcula el área de la zona de paseo.
La Figura muestra en color gris el área correspondiente a la zona de paseo. Esta zona corresponde al área delimitada por dos circunferencias concéntricas, es decir, una corona circular.El área de una corona circular se calcula como sigue: donde
donde 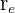 es el radio mayor (radio externo)
es el radio mayor (radio externo)
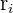 es el radio menor (radio interno).
es el radio menor (radio interno).

Ahora bien, de los datos del problema tenemos: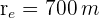
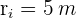
Por lo tanto, el área de la zona de paseo en el parque es: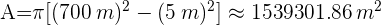
La superficie de una mesa está formada por una parte central cuadrada de 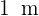 de lado y dos semicírculos adosados en dos lados opuestos. Calcula el área.
de lado y dos semicírculos adosados en dos lados opuestos. Calcula el área.
Dado que la parte central de la mesa es un cuadrado, entonces los dos semicírculos laterales son iguales y forman un solo círculo con diámetro 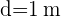 (ver figura).
(ver figura).

El área de la mesa es
 es la longitud de la mesa
es la longitud de la mesa es el diámetro del círculo.
es el diámetro del círculo.
Sustituyendo valores numéricos, obtenemos el área de la mesa: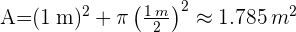
Calcula el área de la parte sombreada, si el radio del círculo mayor mide 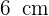 y el radio de los círculos pequeños miden
y el radio de los círculos pequeños miden 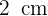 .
.
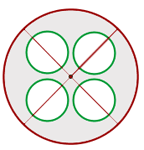
De acuerdo a la figura geométrica dada, el área sombreada se calcula como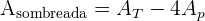
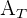 es el área del círculo mayor de radio
es el área del círculo mayor de radio 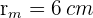
 es el área de cada uno de los círculos pequeños de radio
es el área de cada uno de los círculos pequeños de radio 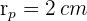
Por lo tanto, tenemos que
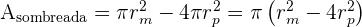 .
.
Finalmente sustituyendo los valores numéricos, se tiene que el área de la parte sombreada es:
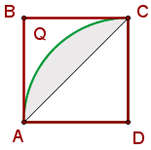
Calcula el área de la parte sombreada, siendo  ,
,  un cuadrado y
un cuadrado y 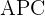 y
y 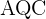 arcos de circunferencia de centros
arcos de circunferencia de centros  y
y  .
.
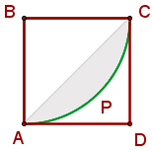
Dado que ambos segmentos circulares son iguales, sin perdida de generalidad podemos analizar cualquiera de estos. Note que cada segmento circular consta de un triángulo isósceles y un sector circular cuya apertura es 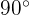 . Por lo tanto,
. Por lo tanto,

Finalmente sustituyendo datos numéricos en la expresión anterior, el área de 1 segmento circular es
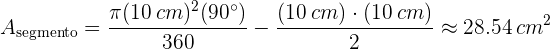
y el área sombreada buscada entonces es
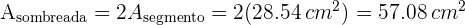
Un satélite de comunicaciones orbita la Tierra en un ángulo de 45° respecto al ecuador. Si la altura del satélite es de 10,000 kilómetros, ¿cuál es la longitud máxima en kilómetros de la trayectoria que cubre en su órbita?
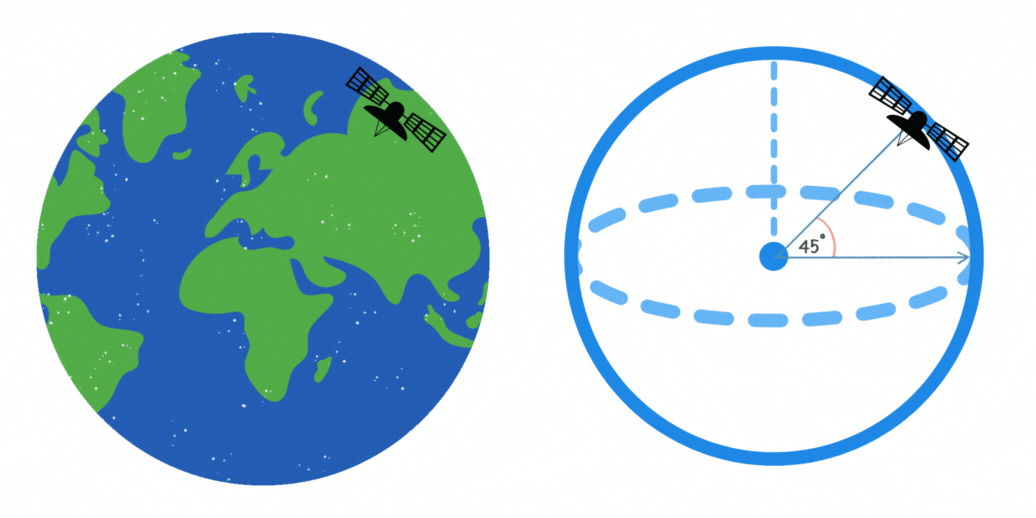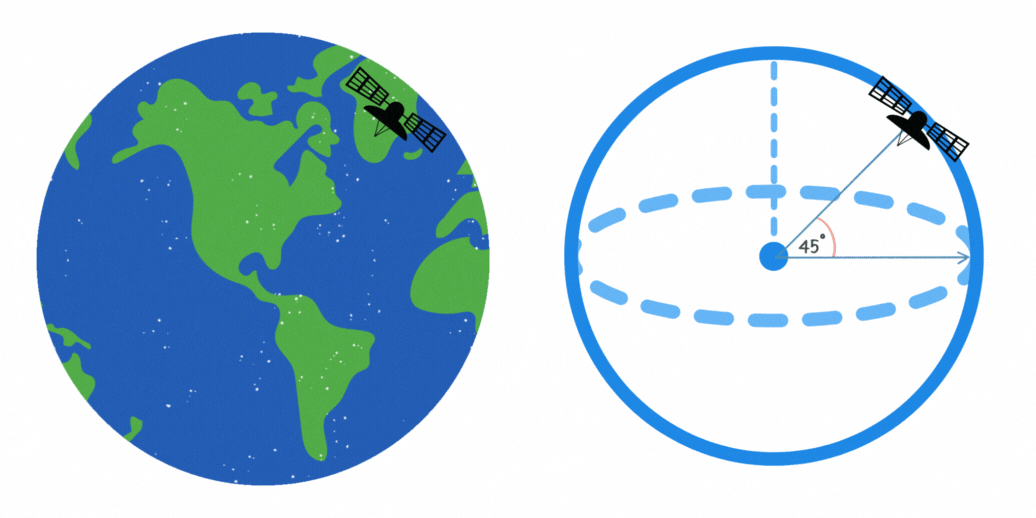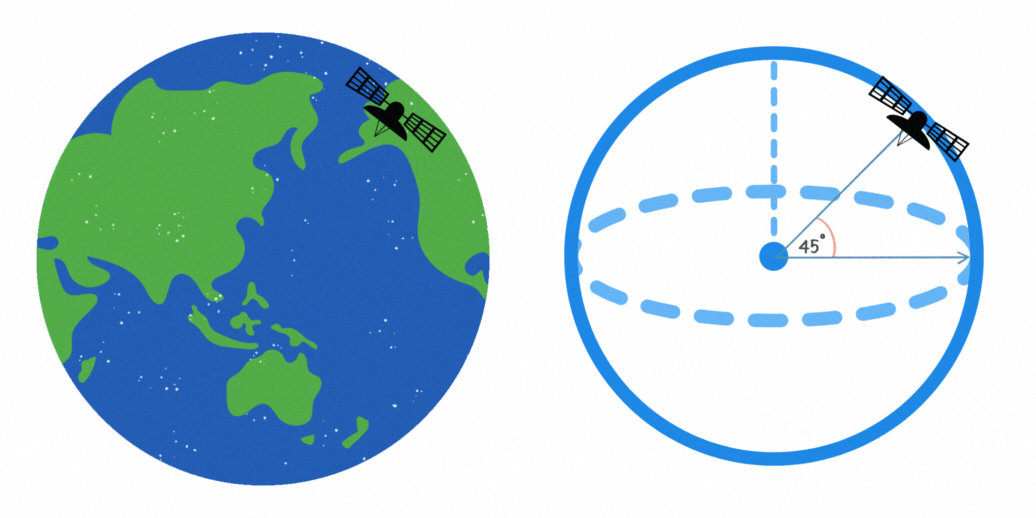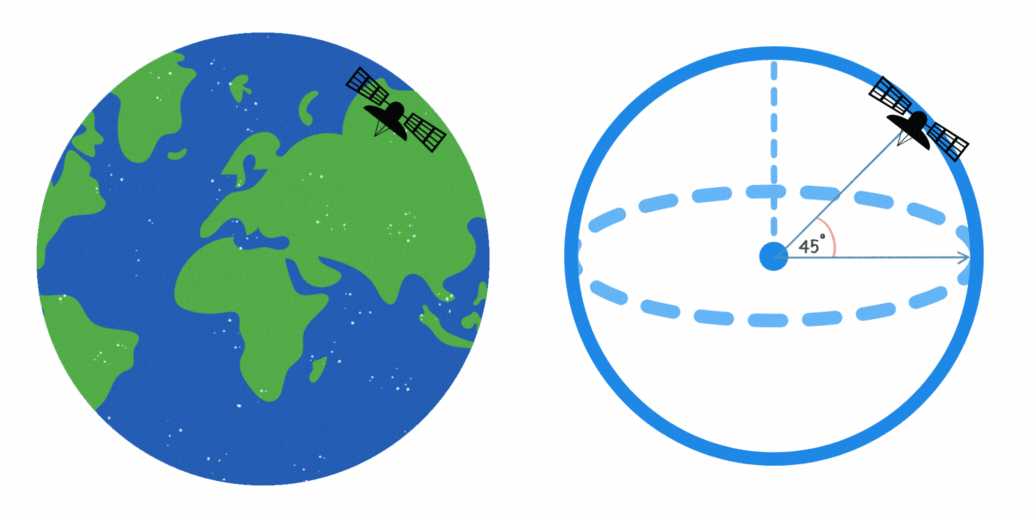
La longitud de la trayectoria del satélite en su órbita se puede calcular con la fórmula del arco de un círculo. Esto se puede apreciar en la figura, ya que el satélite recorre un camino circular de radio constante. La fórmula es
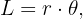
donde 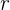 es la distancia del centro de la tierra hasta el satélite,
es la distancia del centro de la tierra hasta el satélite,  es el ángulo en radianes. Recordemos que 45° es equivalente a
es el ángulo en radianes. Recordemos que 45° es equivalente a 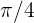 radianes. Por lo tanto, el satélite recorre
radianes. Por lo tanto, el satélite recorre
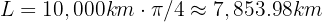
Una noria tiene un radio de 15 metros. Si la noria da 3 vueltas completas, ¿cuánto ha recorrido un pasajero a lo largo de la circunferencia?
La distancia recorrida por el pasajero en la noria se puede calcular usando la circunferencia de la rueda y el número de vueltas. Es decir,
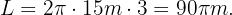
Una bicicleta con ruedas de 26 cm de diámetro recorre 5 km. ¿Cuántas vueltas completas ha dado cada rueda durante este recorrido?
Recordemos que si 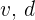 son las vueltas recorridas y el diámetro, respectivamente, la distancia total recorrida se puede calcular mediante
son las vueltas recorridas y el diámetro, respectivamente, la distancia total recorrida se puede calcular mediante
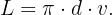
Como conocemos la distancia total recorrida, debemos despejar para 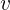 :
:

Un pastel circular se corta en 8 porciones iguales. Si el pastel tiene un radio de 20 centímetros, ¿cuánto mide el arco de cada porción? ¿Cuánta área tiene la parte superior del pastel?
Para calcular el ángulo, simplemente debemos partir 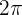 en 8 partes. Por lo que cada rebanada es
en 8 partes. Por lo que cada rebanada es
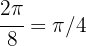
del sector completo. Como tiene un radio de 20 cm, tenemos que el área de este sector es de
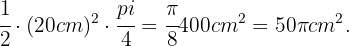
¿Qué radio debe tener una rueda para darle una vuelta completa por el ecuador a la Tierra en 3 revolución?
Primero calculamos la distancia que tiene el ecuador de la Tierra: sabemos que tiene un radio de 6378 km hasta el ecuador. Esto nos dice que debemos recorrer
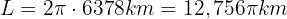
en 3 revoluciones. Es decir, queremos que el radio 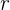 de nuestra rueda sea tal que
de nuestra rueda sea tal que  . Entonces,
. Entonces,
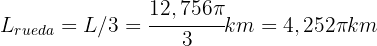
debe ser lo que mide la circunferencia. Por lo que el radio debe ser
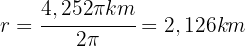
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.