El cálculo del área de polígonos es una habilidad fundamental en la geometría, con aplicaciones en diversas áreas como la arquitectura, el diseño, la agrimensura y muchas otras disciplinas prácticas. Comprender cómo determinar estas áreas no solo refuerza conceptos geométricos básicos, sino que también desarrolla habilidades analíticas y de razonamiento lógico.
En este material encontrarás una serie de ejercicios resueltos que abarcan diferentes tipos de polígonos, como triángulos, cuadriláteros, pentágonos y figuras más complejas. Cada ejercicio está diseñado para ayudarte a aplicar fórmulas específicas, interpretar datos y resolver problemas paso a paso.
Un campo rectangular tiene  m de base y
m de base y  m de altura. Calcular:
m de altura. Calcular:
A Las hectáreas que tiene.
B El precio del campo si el metro cuadrado cuesta  €.
€.
A Calculamos el área del rectángulo, para esto multiplicamos la base por la altura
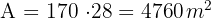
Sabemos que una hectárea es igual a 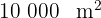 , por lo que el número de hectáreas del rectángulo es
, por lo que el número de hectáreas del rectángulo es
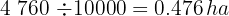
BPara calcular el precio del campo si el metro cuadrado cuesta  €, realizamos
€, realizamos
 €
€
Un campo de baseball tiene un diamante de 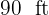 de lado. Encuentra el área del diamante.
de lado. Encuentra el área del diamante.
El diamante de un estadio de baseball es en realidad un cuadrado, por los que al área solicitada es
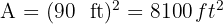
Una cancha de baloncesto tiene 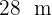 de largo por
de largo por 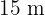 de ancho. Si el mantenimiento por metro cuadrado tiene un costo de 12 €, encuentra el costo del mantenimiento de la cancha.
de ancho. Si el mantenimiento por metro cuadrado tiene un costo de 12 €, encuentra el costo del mantenimiento de la cancha.
El área total de la cancha de baloncesto es
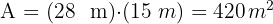
El costo total del mantenimiento es
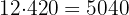 €
€
Un campo de futbol de 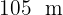 de largo por
de largo por 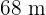 de ancho, emplea 55 000 litros de agua al día para su riego. Una nueva tecnología en aspersores permite regar un metro cuadrado con cinco litro de agua. ¿Cuántos litros de agua al día se ahorrará con esta nueva tecnología?
de ancho, emplea 55 000 litros de agua al día para su riego. Una nueva tecnología en aspersores permite regar un metro cuadrado con cinco litro de agua. ¿Cuántos litros de agua al día se ahorrará con esta nueva tecnología?
El área total del campo de futbol es
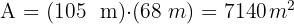
El ahorro total de litros es
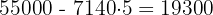 litros
litros
Un litro de pintura rinde cinco metros cuadrados de superficie para pintar. ¿Cuántos litros de pintura se requieren para pintar una pared de diez metros de largo por cuatro de alto?
El área total de la pared es
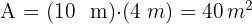
La cantidad de litros requeridos es
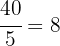 litros
litros
Calcula el número de baldosas cuadradas, de  cm, de lado que se necesitan para enlosar una superficie rectangular de
cm, de lado que se necesitan para enlosar una superficie rectangular de  m de base y
m de base y  m de altura.
m de altura.
1 Calculamos el área del rectángulo, para esto multiplicamos la base por la altura
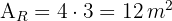
2Sabemos que 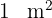 es igual a
es igual a  , por lo que el área del rectángulo en centímetros cuadrados es
, por lo que el área del rectángulo en centímetros cuadrados es
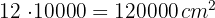
3Calculamos el área de una baldosa
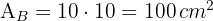
4Para calcular el número de baldosas requeridas, dividimos el área del rectángulo entre el área de una baldosa
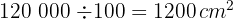
así, se requieren 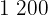 baldosas
baldosas
Hallar el área de un triángulo rectángulo isósceles cuyos lados miden  cm cada uno.
cm cada uno.
1 Dibujamos el triángulo rectángulo isósceles

2Observamos que los lados iguales corresponden a la base y la altura del triángulo
3Calculamos el área del triángulo, el cual es igual al producto de su base por su altura entre dos
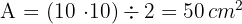
El perímetro de un triángulo equilátero mide  dm y la altura mide
dm y la altura mide  cm. Calcula el área del triángulo.
cm. Calcula el área del triángulo.
1 Dibujamos el triángulo equilátero

2Observamos que el perímetro está dado en  y la altura en
y la altura en  . Convertimos el perímetro a centímetros
. Convertimos el perímetro a centímetros
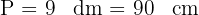
Para calcular el área del triángulo, necesitamos conocer su base y su altura. Como el triángulo es equilátero, sus tres lados son iguales, luego un lado se obtiene dividiendo el perímetro entre tres
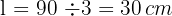
Calculamos el área del triángulo, el cual es igual al producto de su base por su altura entre dos

Calcula el número de árboles que pueden plantarse en un terreno rectangular de  de largo y
de largo y  de ancho si cada planta necesita para desarrollarse
de ancho si cada planta necesita para desarrollarse 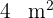 .
.
1 Calculamos el área del terreno rectangular, el cual es igual al producto de su largo por su ancho
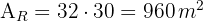
Observamos que cada planta necesita 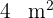 , por lo que para calcular el número de árboles dividimos el área del terreno entre cuatro
, por lo que para calcular el número de árboles dividimos el área del terreno entre cuatro
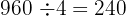
Así, el número de árboles que se puede plantar es 
El área de un trapecio es 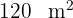 , la altura
, la altura  , y la base menor mide
, y la base menor mide  . ¿Cuánto mide la otra base?.
. ¿Cuánto mide la otra base?.
1 Escribimos la fórmula del área de un trapecio la cual es igual a la mitad del producto de la altura por la suma de las bases

2Sustituimos los datos conocidos
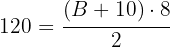
3Simplificamos el lado derecho, dividiendo ocho entre dos

4Queremos despejar  , por lo que dividimos ambos lados entre cuatro y obtenemos
, por lo que dividimos ambos lados entre cuatro y obtenemos

5Restamos diez a ambos lados y obtenemos
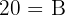
Así, la otra base mide 
Calcular el área de un paralelogramo cuya altura mide  cm y su base mide
cm y su base mide  veces su altura.
veces su altura.
1 Para calcular el área necesitamos conocer la base y la altura. La altura mide  y la base mide tres veces su altura, luego el valor de la base es
y la base mide tres veces su altura, luego el valor de la base es
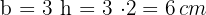
2Calculamos el área, el cual es igual al producto de la base y la altura
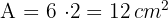
Calcula el área de un rombo cuya diagonal mayor mide  cm y cuya diagonal menor es la mitad de la mayor.
cm y cuya diagonal menor es la mitad de la mayor.
1 Para calcular el área necesitamos conocer la diagonal mayor y la diagonal menor del rombo. La diagonal mayor mide 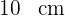 y la menor mide la mitad de la mayor, luego el valor de la diagonal menor es
y la menor mide la mitad de la mayor, luego el valor de la diagonal menor es

2Calculamos el área, el cual es igual a la mitad de producto de las diagonales

En el centro de un jardín cuadrado de  m de lado hay una piscina también cuadrada, de
m de lado hay una piscina también cuadrada, de  m de largo. Calcula el área del jardín.
m de largo. Calcula el área del jardín.
1 Representamos gráficamente el problema y notamos que el área total es igual a área del jardín más el área de la piscina
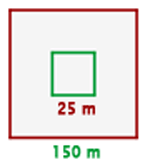
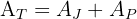
2Calculamos el área total, el cual es igual al producto de los lados del cuadrado

3Calculamos el área de la piscina, el cual es igual al producto de los lados del cuadrado
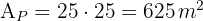
4Así, el área del jardín es igual el área total menos el área de la piscina
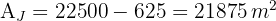
Calcula el área del cuadrilátero que resulta de unir los puntos medios de los lados de un rectángulo cuya base y altura miden  y
y  cm.
cm.
1 Representamos gráficamente el problema y notamos que el área total es igual a cuatro triángulos rectángulos de base  y altura
y altura 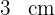
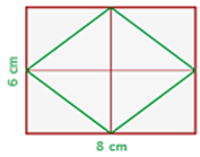
2Calculamos el área del triángulo
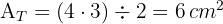
3Calculamos el área del cuadrilátero

Cuánto vale el área de la parte subrayada de la figura, si el área del hexágono es de 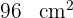 .
.

1 Observamos que el hexágono esta compuesto por seis triángulos iguales
2 Calculamos el área de un triángulo

3Calculamos el área subrayada
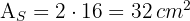
Una zona boscosa tiene forma de trapecio, cuyas bases miden  m y
m y  m. La anchura de la zona mide
m. La anchura de la zona mide  m. Se construye un paseo de
m. Se construye un paseo de  m de ancho perpendicular a las dos bases. Calcula el área de la zona arbolada que queda.
m de ancho perpendicular a las dos bases. Calcula el área de la zona arbolada que queda.
1 Representamos gráficamente el problema y notamos que el área del trapecio es igual a la suma del área de la zona arbolada y el área del paseo
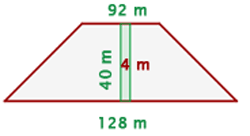
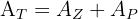
2Calculamos el área del trapecio
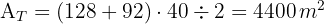
3Calculamos el área del paseo,

4Calculamos el área de la zona arbolada

Un jardín rectangular tiene por dimensiones  m y
m y  m. El jardín está atravesado por dos caminos perpendiculares que forman una cruz. Uno tiene un ancho de
m. El jardín está atravesado por dos caminos perpendiculares que forman una cruz. Uno tiene un ancho de  dm y el otro
dm y el otro  dm. Calcula el área del jardín.
dm. Calcula el área del jardín.
1 Representamos gráficamente el problema y notamos que el área del jardín es igual a el área del rectángulo menos el área de los caminos más el área de la intersección de los caminos
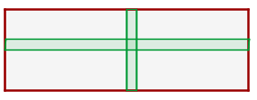

2Calculamos el área del rectángulo

3Calculamos el área del primer camino
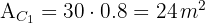
4Calculamos el área del segundo camino
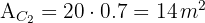
5Calculamos el área de la intersección de los caminos

6Calculamos el área del jardín
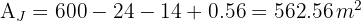
Dado el cuadrado  , de
, de  m de lado, se une
m de lado, se une  , punto medio del segmento
, punto medio del segmento  , con el vértice
, con el vértice  . Calcular el área del trapecio formado.
. Calcular el área del trapecio formado.
1 Representamos gráficamente el problema y notamos que el área del trapecio es igual a el área del cuadrado menos el área de un triángulo rectángulo


2Calculamos el área del cuadrado

3Calculamos el área del triángulo
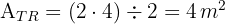
4Calculamos el área del trapecio
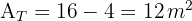
Calcula la cantidad de pintura necesaria para pintar la fachada de este edificio sabiendo que se gastan  kg de pintura por
kg de pintura por  .
.

1 Notamos que el área del edificio está formado un triángulo de base  y altura
y altura 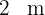 ; dos rectángulos de base
; dos rectángulos de base  y altura
y altura 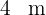 ; y dos triángulos rectángulos de base
; y dos triángulos rectángulos de base 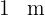 y altura
y altura 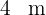

2Calculamos el área del triángulo
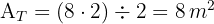
3Calculamos el área del rectángulo

4Calculamos el área del triángulo rectángulo

5Calculamos el área del edificio

6Calculamos los kilogramos de pintura requeridos para pintar el edificio
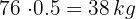
Hallar el perímetro y el área de la figura:
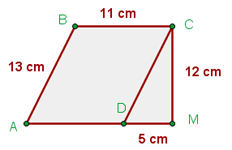
1 Notamos que la figura está formando un paralelogramo de base  y altura
y altura 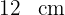 ; un triángulo rectángulo de base
; un triángulo rectángulo de base  y altura
y altura 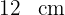 , por lo que su área es
, por lo que su área es

2Calculamos el área del triángulo

3Calculamos el área del paralelogramo
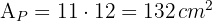
4Calculamos el área de la figura
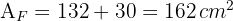
5Calculamos el perímetro
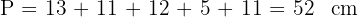
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
pueden dejar los puntos mas claros
Hola con todo gusto te apoyamos si tienes alguna duda, solo menciona el número de ejercicio y te lo explicamos mas detalladamente.
La respuesta de la pregunta de la número 8 es 45 unidades cuadradas y coloco 45 y sale en rojo no entiendo
Hola tu respuesta esta bien, disculpa por la respuesta estamos trabajando en ello.
8 un rectangulo tiene ancho 3 unidades.el largo del rectangulo es 5 vaces su ancho.
Cual es el area del rectangulo.
45 u2
Si, así es esa es la respuesta, estamos trabajando en ello.
Hola gracias por el aporte, estamos trabajando en ello, una disculpa.