
Una pequeña noción sobre funciones
Hay muchas cosas en la vida diaria que se relacionan entre sí, por ejemplo, el tamaño de una casa con su precio, la edad de una persona con su condición física, el tráfico en una ciudad y el número de coches que hay en ella, incluso el precio de un servicio de taxi ejecutivo y la demanda que existe en ese momentos (Uber). Estos son ejemplos de "funciones" que se presentan día a día y podríamos no darnos cuenta.
De forma informal, podríamos ver una función como una máquina a la cual le damos un objeto y ésta nos arroja otro objeto, como si fuera una máquina dispensadora de golosinas, le arrojamos el dinero, seleccionamos el producto y está nos despacha.

Esto nos da una noción sobre qué sería una función, un tipo de máquina que relaciona objetos, ¿qué objetos? Los que le damos con los que nos regresa. Sin embargo, de manera formal, el concepto de función debe cumplir ciertas restricciones (propiedades), una de ellas es, por ejemplo, que cada que le demos un objeto, la función solo debe devolvernos un único objeto; sería muy raro darle una moneda y pedirle un chocolate a una máquina dispensadora de golosinas y que ésta nos arroje un chocolate, unas galletas y hasta un refresco, ¿no?
Definición de relación y de función
Para poder definir formalmente qué es una función, primero debemos definir una relación entre conjuntos.
Dados dos conjuntos  y
y  , llamamos relación de
, llamamos relación de  en
en  cualquier correspondencia que haya entre algunos de los elementos de
cualquier correspondencia que haya entre algunos de los elementos de  con los elementos de
con los elementos de  .
.
Ejemplos
1. Consideremos los conjunto 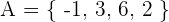 y
y 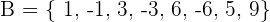 , y la relación dada por la siguiente imagen
, y la relación dada por la siguiente imagen
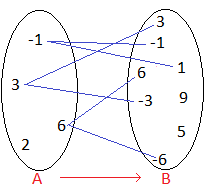
Notemos que no todos los elementos de  están relacionados con elementos de
están relacionados con elementos de  , por ejemplo, el elemento
, por ejemplo, el elemento 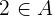 no tiene imagen en
no tiene imagen en  .
.
Nota. En una relación no es necesario que todos los elementos de ambos conjuntos estén relacionados.
También podemos escribir la relación como un conjunto, en este caso la relación estaría dada por el conjunto 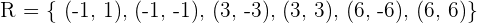 . Notemos que, para cada par ordenado, la primer entrada, contando de izquierda a derecha, es un elemento de
. Notemos que, para cada par ordenado, la primer entrada, contando de izquierda a derecha, es un elemento de  , mientras que el de la segunda entrada es el elemento de
, mientras que el de la segunda entrada es el elemento de  con el cual se relaciona.
con el cual se relaciona.
2. Consideremos los conjunto  y
y 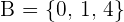 , y la relación dada por la siguiente imagen
, y la relación dada por la siguiente imagen

En este caso, todos los elementos de  están relacionados con elementos de
están relacionados con elementos de  .
.
Esta relación dada como conjunto estaría dada por 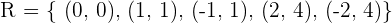 .
.
Ahora que sabemos qué es una relación, podemos definir una función entre conjuntos.
Dados dos conjuntos  y
y  , una función de
, una función de  en
en  es una relación que cumple las siguientes dos propiedades:
es una relación que cumple las siguientes dos propiedades:
- Todo elemento del conjunto
 debe de estar relación con un elemento del conjunto
debe de estar relación con un elemento del conjunto  .
.
- Ningún elemento del conjunto
 debe de estar relación con mas de un elemento del conjunto
debe de estar relación con mas de un elemento del conjunto  .
.
Estas dos propiedades pueden reducirse a decir que todo elemento del conjunto  debe de estar relación con un único elemento del conjunto
debe de estar relación con un único elemento del conjunto  .
.
Dada una función de un conjunto  en un conjunto
en un conjunto  , al conjunto
, al conjunto  se le conoce como dominio, mientras que al conjunto
se le conoce como dominio, mientras que al conjunto  como codominio (o contradominio).
como codominio (o contradominio).
Usualmente a una función se le denota por  y para denotar que esta va de un conjunto
y para denotar que esta va de un conjunto  en un conjunto
en un conjunto  escribimos
escribimos
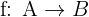 .
.
Además, si 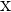 es un elemento en
es un elemento en  , entonces, al elemento con el cual se relaciona en
, entonces, al elemento con el cual se relaciona en  lo denotamos por
lo denotamos por
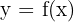 ,
,
esto lo podemos interpretar como 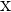 el cual se relaciona con
el cual se relaciona con 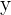 bajos las reglas dadas por
bajos las reglas dadas por  .
.
Cuando utilizamos la notación 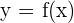 , a
, a 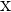 la conocemos como la variable independiente, mientras que a
la conocemos como la variable independiente, mientras que a 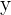 la conocemos como la variable dependiente.
la conocemos como la variable dependiente.
Ejemplos
1. El ejemplo 1 de relaciones no es una función ya que hay elementos del dominio,  , que no están relacionados con ningún elemento del codominio,
, que no están relacionados con ningún elemento del codominio,  . Además, hay elementos en
. Además, hay elementos en  que se relacionan con más de un elemento en
que se relacionan con más de un elemento en  .
.
2. El ejemplo 2 de relaciones sí es una función ya que todos los elementos del dominio,  , están relacionados con un único elemento del codominio,
, están relacionados con un único elemento del codominio,  . De hecho, en este caso, podemos ver que, para todo
. De hecho, en este caso, podemos ver que, para todo  , su relación con los elementos
, su relación con los elementos 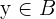 está dada por
está dada por 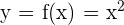 .
.
3. Consideremos el conjunto 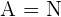 , al conjunto
, al conjunto 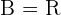 y a
y a 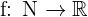 dada por
dada por  . ¿Es una función? Bueno, eso depende, veamos por qué.
. ¿Es una función? Bueno, eso depende, veamos por qué.
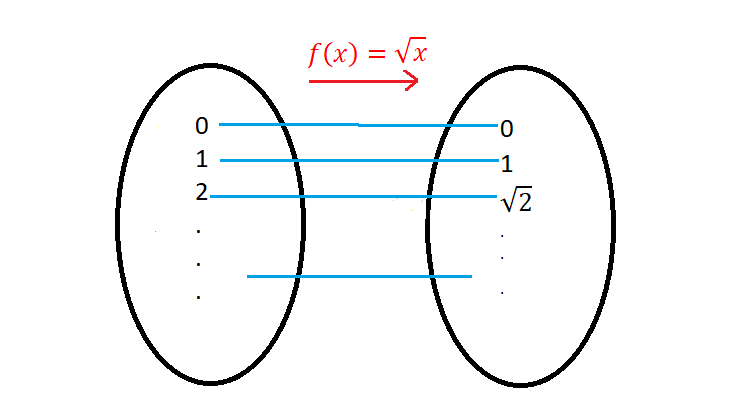
- Primero, notemos que para todo número, por ejemplo,
 , se tiene que
, se tiene que  , esto ya que
, esto ya que  . Por lo tanto, en este caso, para cada elemento del dominio le estaríamos asignando dos elementos del codiminio y no sería una función.
. Por lo tanto, en este caso, para cada elemento del dominio le estaríamos asignando dos elementos del codiminio y no sería una función.
- Sin embargo, cuando se habla de la raíz de un número, solemos considerar únicamente la parte positiva, por lo tanto, a menos que se especifique lo contrario, para todo número, por ejemplo,
 , se tendrá que
, se tendrá que 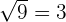 . Así, tendríamos que
. Así, tendríamos que  sí es una función ya que por lo mencionado tendríamos una única correspondencia para todo elemento en el dominio, además, como definimos de un inicio
sí es una función ya que por lo mencionado tendríamos una única correspondencia para todo elemento en el dominio, además, como definimos de un inicio 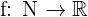 ya estamos considerando todo el dominio
ya estamos considerando todo el dominio 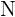 .
.
- Si queremos considerar únicamente la parte negativa de la raíz, debemos definir
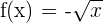 , en este caso, al igual que en el anterior, también tendríamos una función.
, en este caso, al igual que en el anterior, también tendríamos una función.
Si una función cumple que tanto su dominio como su codominio son subconjuntos de los reales ( ), entonces decimos que tenemos una función real.
), entonces decimos que tenemos una función real.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.
Podrían mostrar los pares ordenados para graficarlo, gracias