
Representa las funciones

Grafiquemos 
Hacemos una tabla para calcular dos puntos de la gráfica: 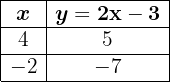
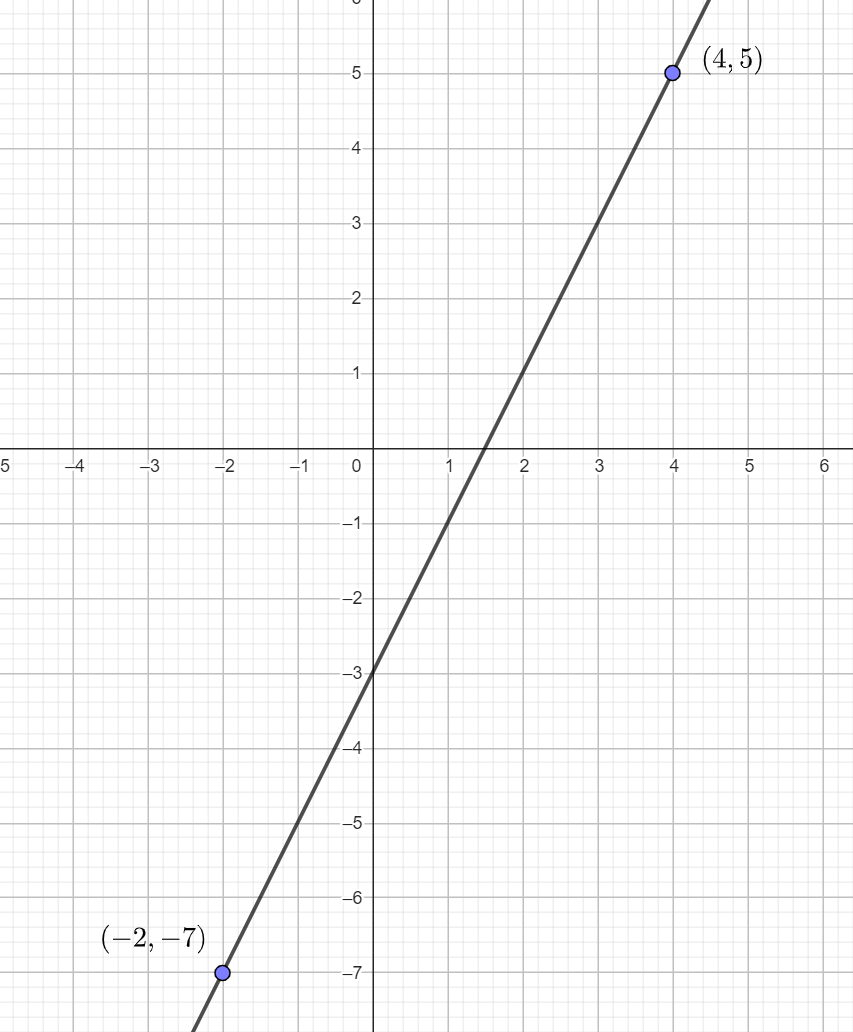
Representamos la recta a partir de los puntos (4,5) y (-2, -7)
Representa la recta que pasa por los puntos 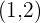 y
y 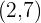
Primero tenemos que hallar la pendiente  y la ordenada
y la ordenada  de la ecuación
de la ecuación 
Consideramos el primer punto con  ,
, 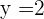 , y sustituimos en nuestra ecuación
, y sustituimos en nuestra ecuación 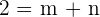
Ahora consideremos el segundo punto,  ,
, 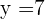 ,
, 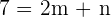 obteniendo así, un sistema de ecuaciones lineales
obteniendo así, un sistema de ecuaciones lineales 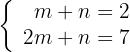
Resolvemos utilizando el método de reducción 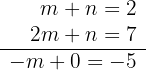
De donde concluimos que 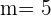 y por tanto,
y por tanto, 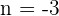 , de aquí la función buscada seria
, de aquí la función buscada seria 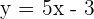

Representemos la función 
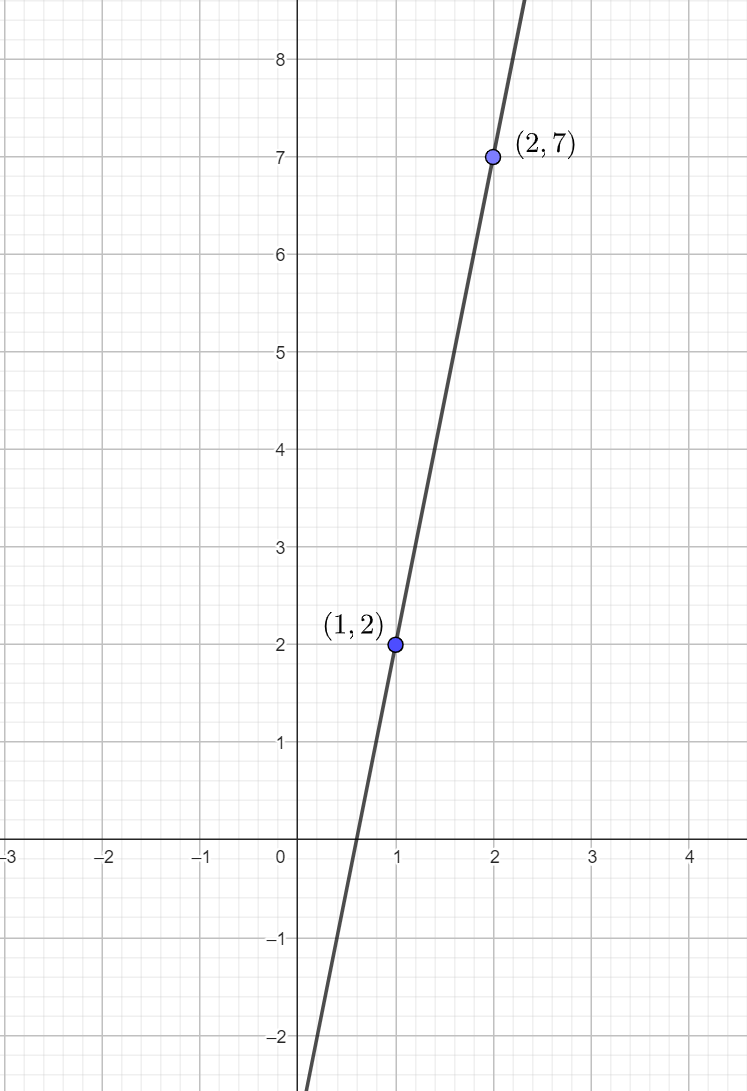
Similar a la función identidad pero de signo contrario, tabulamos para obtener la recta 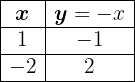
Representamos la recta a partir de los puntos (1,-1) y (-2, 2)
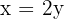
Primero despejamos para que nos quede en función de  , obteniendo
, obteniendo 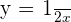 tabulamos dos puntos de la recta
tabulamos dos puntos de la recta 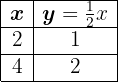
Y representamos la recta a partir de los puntos
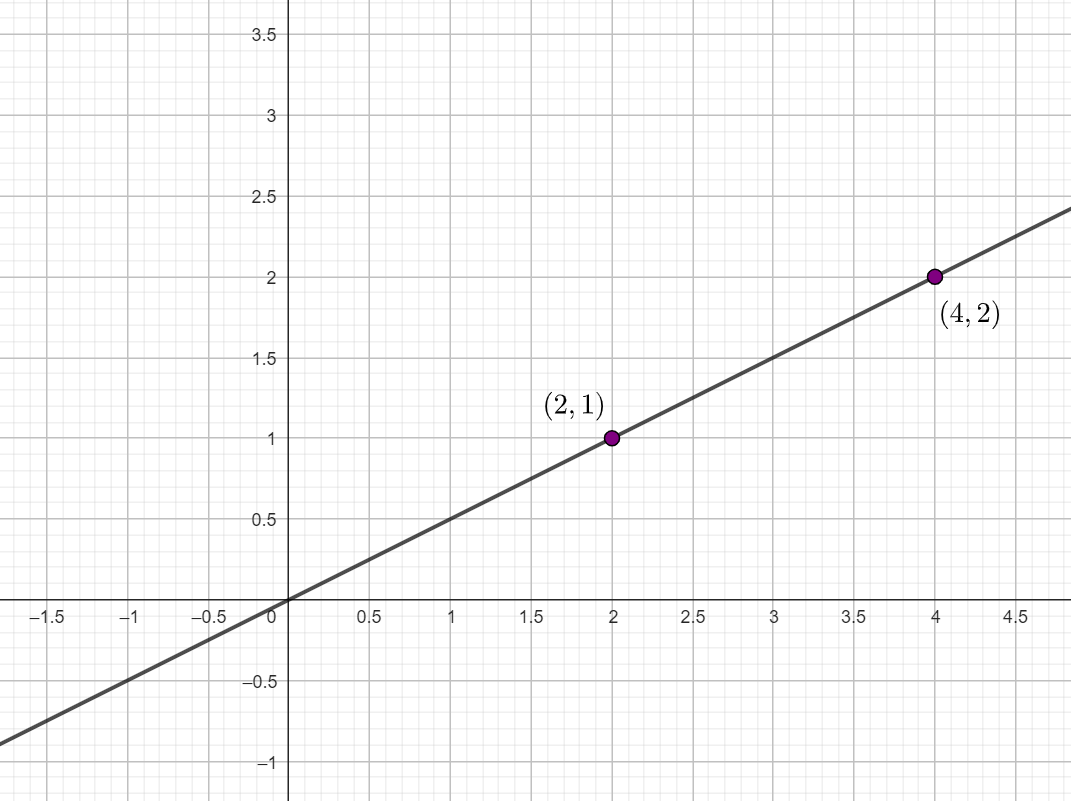
Representa la función lineal que pasa por los puntos 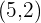 y
y 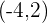
Primero calculemos la pendiente  , recordemos que
, recordemos que 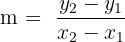 sustituyendo nuestros puntos
sustituyendo nuestros puntos 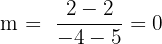
Es decir, tenemos pendiente cero y por tanto se trata de una recta horizontal, y donde el valor de  es constante, es decir
es constante, es decir 
Y su grafica seria 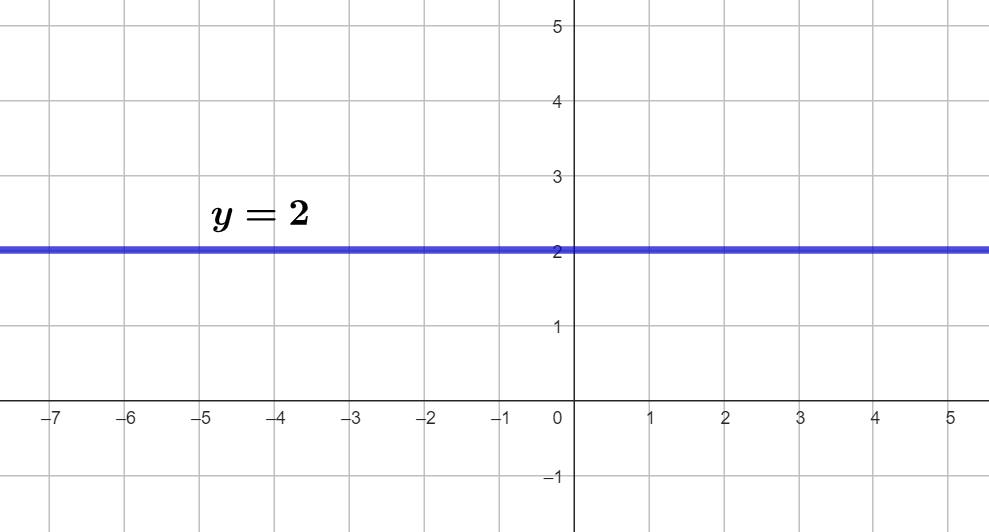
Representa la recta que pasa por los puntos 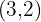 y
y 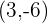
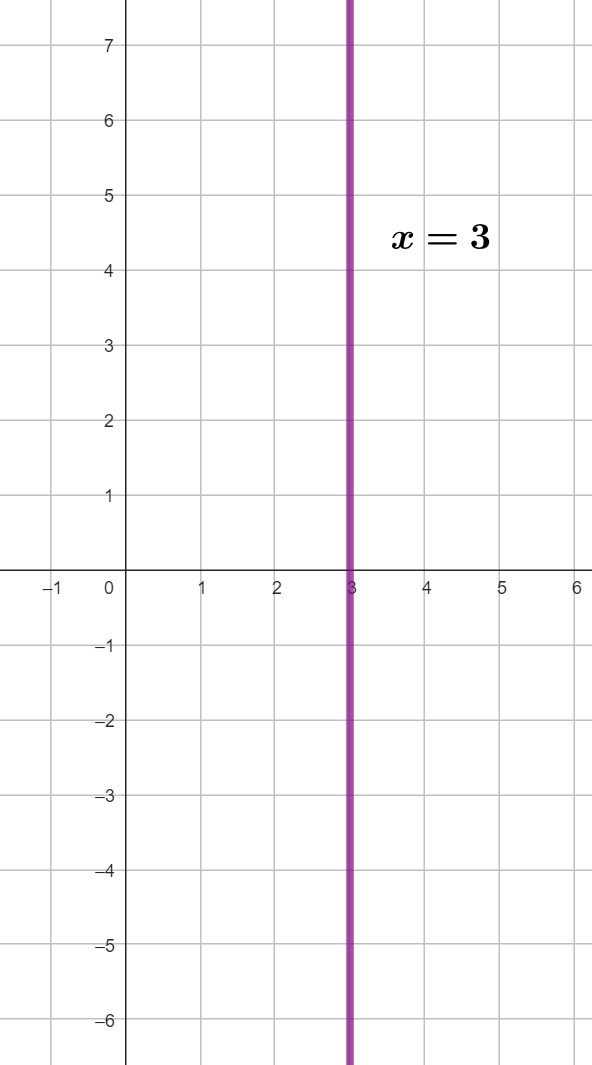
Notemos que la variable  en los puntos es la misma, es decir, es constante. Esto quiere decir que se trata de una recta cuyo valor en
en los puntos es la misma, es decir, es constante. Esto quiere decir que se trata de una recta cuyo valor en  siempre es el mismo, en este caso
siempre es el mismo, en este caso  por lo que se trata de un recta constante vertical. Y se ve de la siguiente manera
por lo que se trata de un recta constante vertical. Y se ve de la siguiente manera
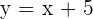
Representa la función a fin 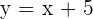
Similar a la función identidad pero recorrida 5 unidades hacia arriba, para mas claridad, tabulemos un par de puntos 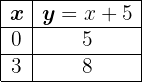
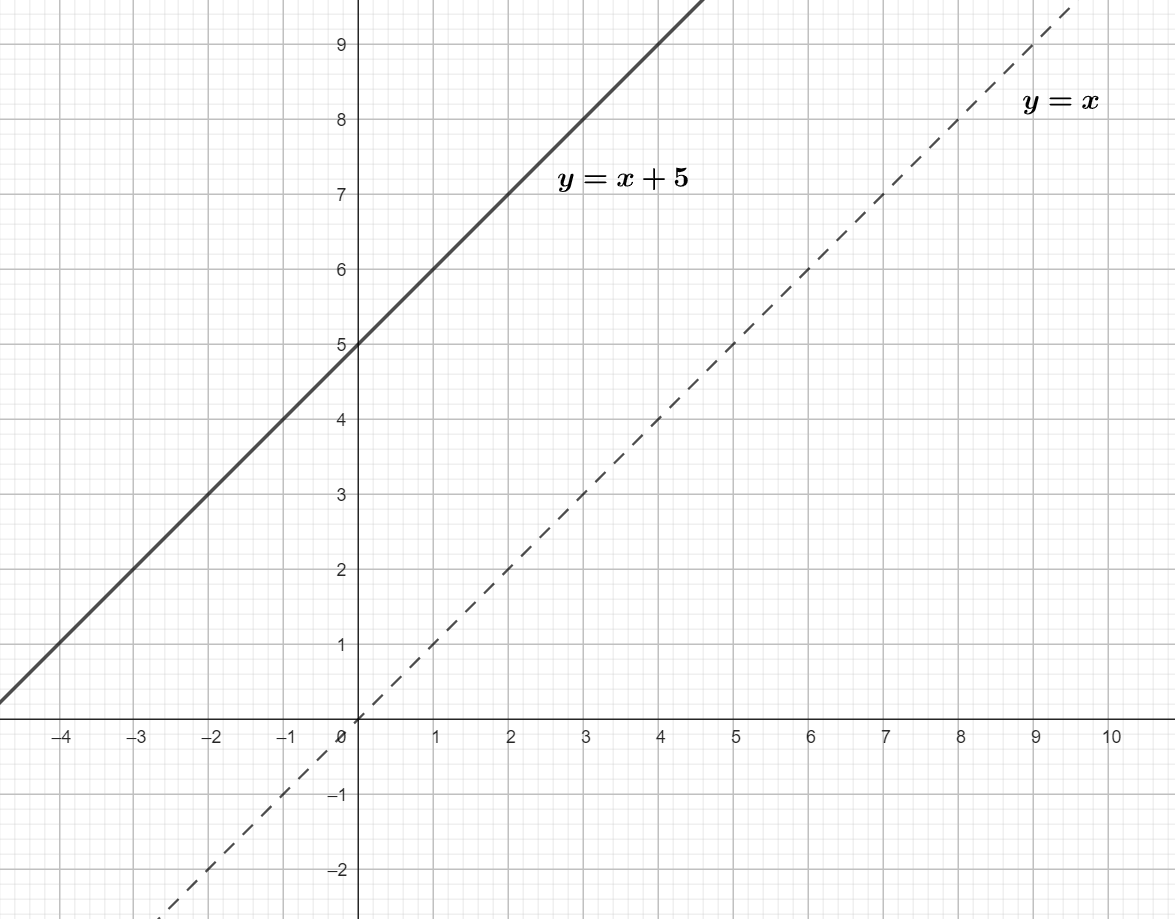
Es decir, la grafica se ve de la siguiente manera

Representa la función lineal: 
Para graficar de forma eficiente, elaboramos una tabla con los valores que toma la función variando 

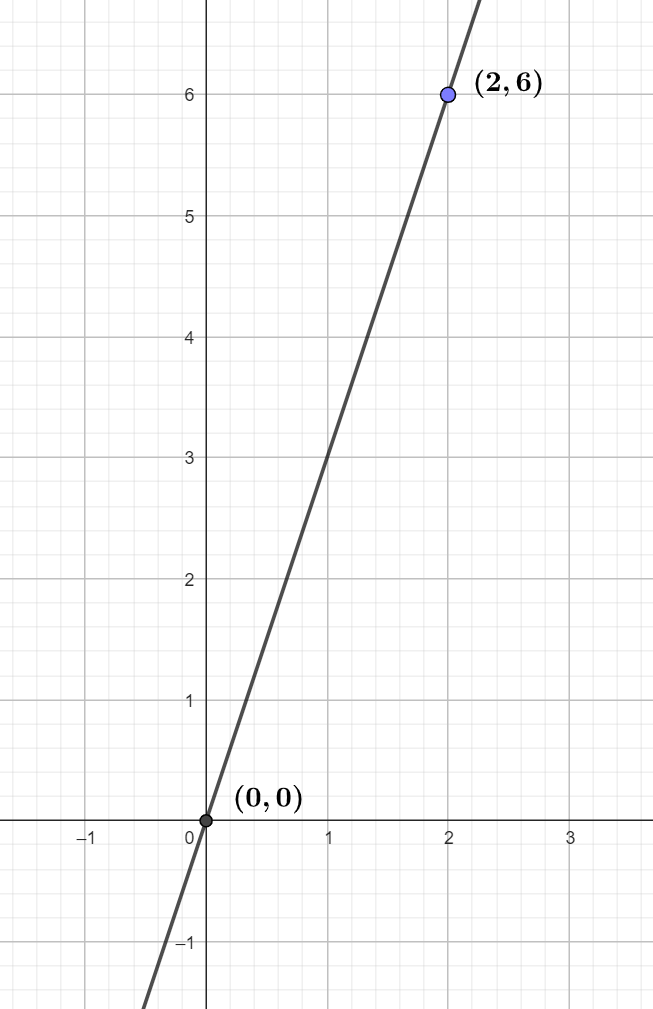
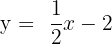
Representemos la función afín 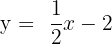
Para poder graficar de una forma eficiente, elaboramos una tabla donde a la izquierda colocaremos los valores de x (cualquiera que nosotros queramos) y del lado derecho el valor que toma y, después de evaluar el valor asignado a x en nuestra función.
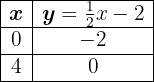
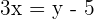
Primero despejamos para que quede en función de la variable  , obteniendo
, obteniendo 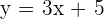
Para poder graficar de una forma eficiente, elaboramos una tabla donde a la izquierda colocaremos los valores de  (cualquiera que nosotros queramos) y del lado derecho el valor que toma
(cualquiera que nosotros queramos) y del lado derecho el valor que toma  , después de evaluar el valor asignado a
, después de evaluar el valor asignado a  en nuestra función.
en nuestra función.
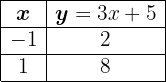
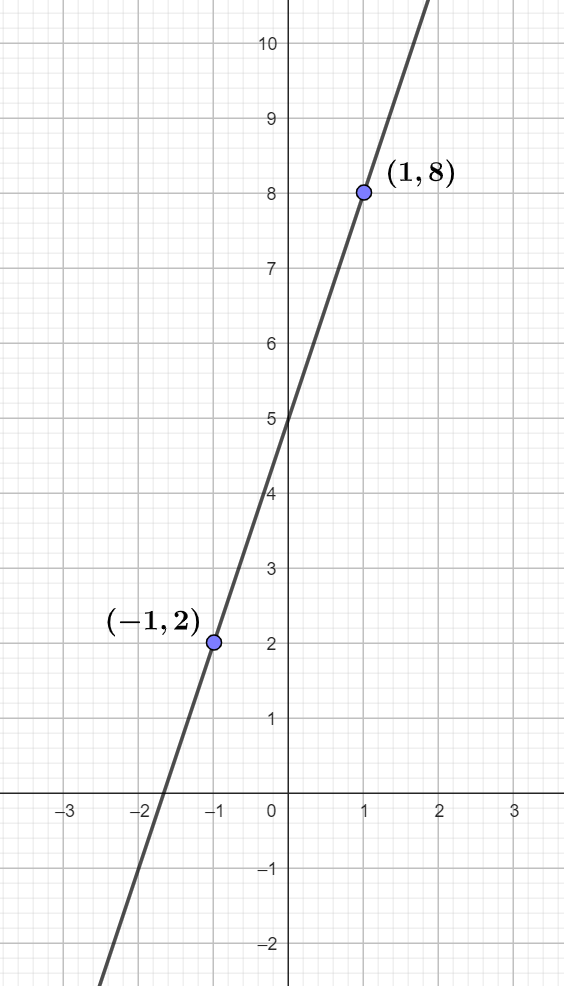
Representa la función lineal que pasa por el puto 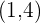 y por el origen.
y por el origen.
Puesto que la recta pasa por el origen, uno de sus puntos es  , ahora bien, con estos datos hallemos la pendiente
, ahora bien, con estos datos hallemos la pendiente  y la ordenada
y la ordenada  de la ecuación
de la ecuación  Consideramos el primer punto con
Consideramos el primer punto con  ,
, 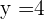 , y sustituimos en nuestra ecuación
, y sustituimos en nuestra ecuación 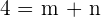 Ahora consideremos el segundo punto que es el origen,
Ahora consideremos el segundo punto que es el origen, 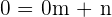 es decir,
es decir, 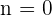 y por tanto
y por tanto 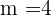 . Con esto nuestra recta tiene como ecuacion
. Con esto nuestra recta tiene como ecuacion 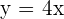
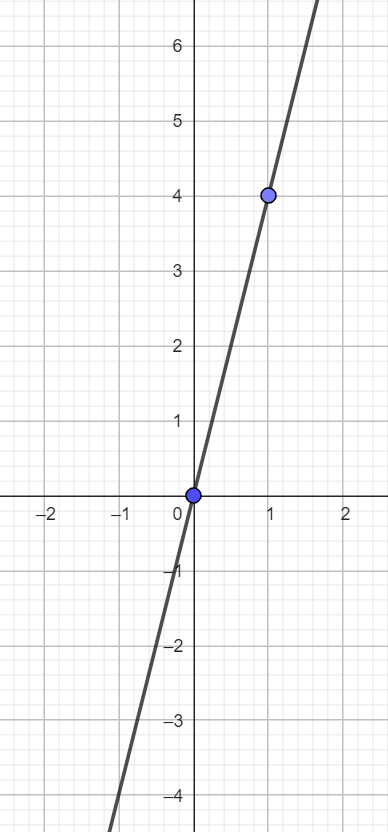
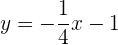
Representa la función afín: 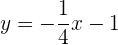
Para graficar de una forma eficiente, elaboramos una tabla donde a la izquierda colocaremos los valores de  (cualquiera que nosotros queramos) y del lado derecho el valor que toma
(cualquiera que nosotros queramos) y del lado derecho el valor que toma  después de evaluar el valor asignado a
después de evaluar el valor asignado a  en nuestra función.
en nuestra función.
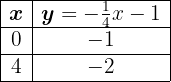
Problemas con funciones lineales
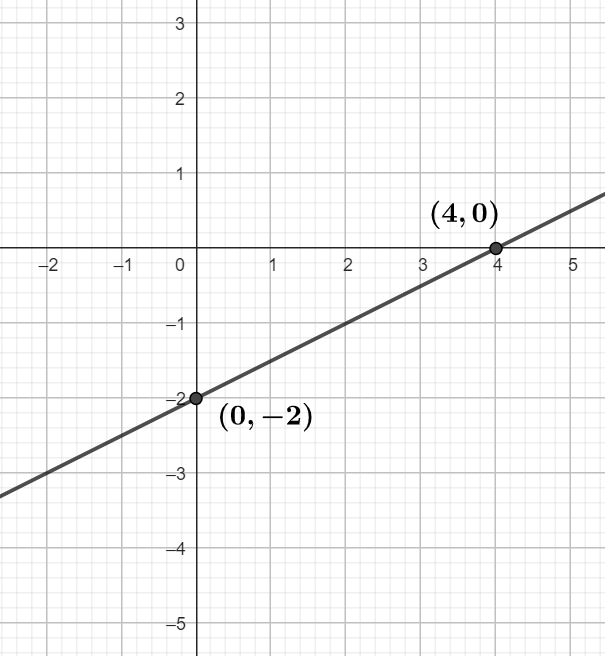
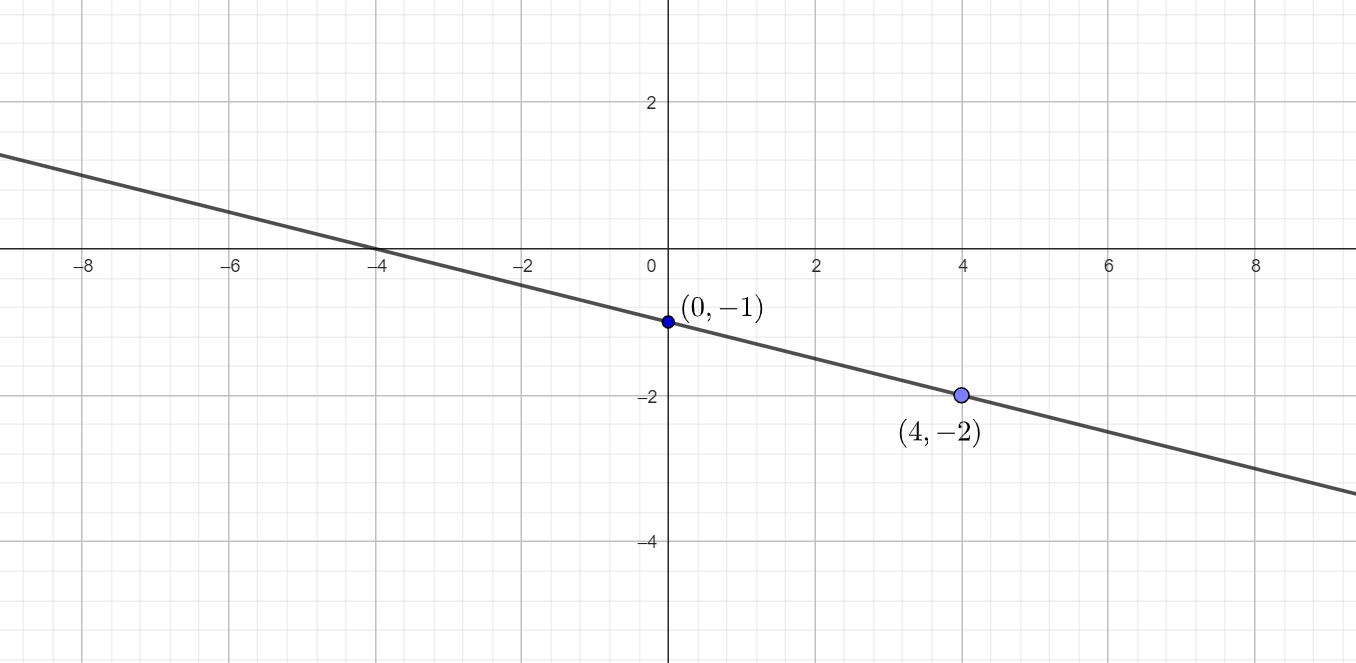
Calcula los puntos de corte con los ejes de la función lineal
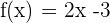
Corta el eje Y cuando la variable  toma el valor de cero, por lo tanto
toma el valor de cero, por lo tanto 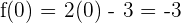
Es decir, corta al eje Y en el punto  .
.
Ahora bien, veamos en que punto corta al eje X, para esto resolvemos 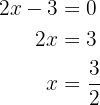
Es decir, es el punto 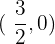 .
.
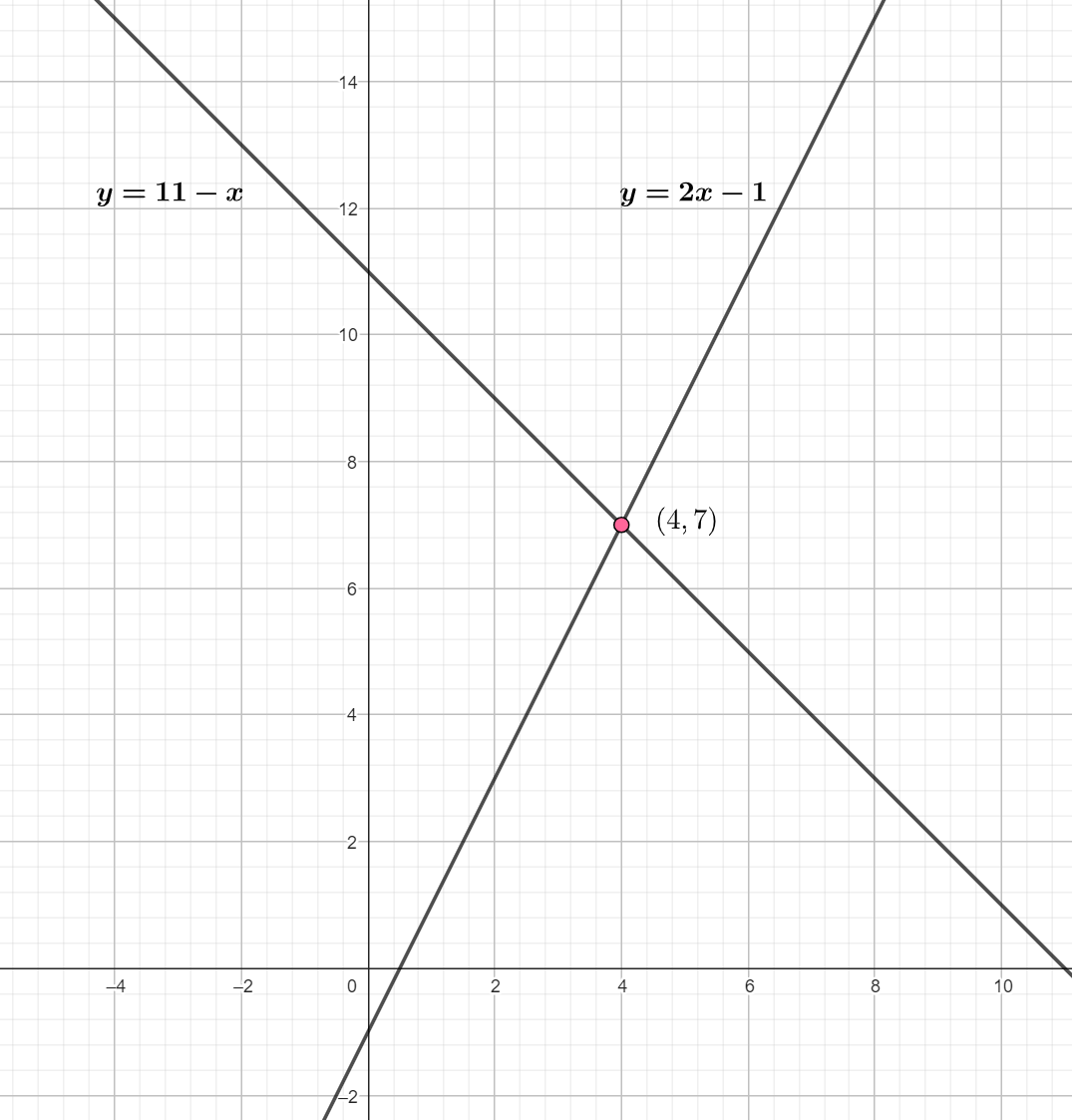
Cual es el punto donde se corta las siguientes dos rectas?
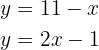
Queremos encontrar el punto donde las rectas tienen el mismo valor, por lo tanto, las igualamos 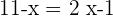
Resolvemos 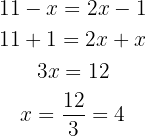
Y así obtenemos la primera coordenada del punto, que es  y para la coordenada
y para la coordenada  calculamos su imagen en alguna de las dos rectas,
calculamos su imagen en alguna de las dos rectas, 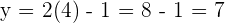
De aquí concluimos que su punto de corte es 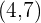 .
.
Calcula y representa la función lineal cuya gráfica es una recta que pasa por los puntos 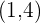 y
y 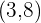
Recordemos que la forma general de la recta es 
Y para resolver este problema debemos calcular la pendiente  y la ordenada
y la ordenada  .
.
Comenzamos sustituyendo en la ecuación el primer punto 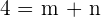
Ahora el segundo punto 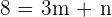
De aquí obtenemos un sistema de ecuaciones lineales 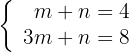
Resolvemos y obtenemos que  , sustituimos esto en alguna de las ecuaciones y se tendra que
, sustituimos esto en alguna de las ecuaciones y se tendra que 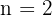 .
.
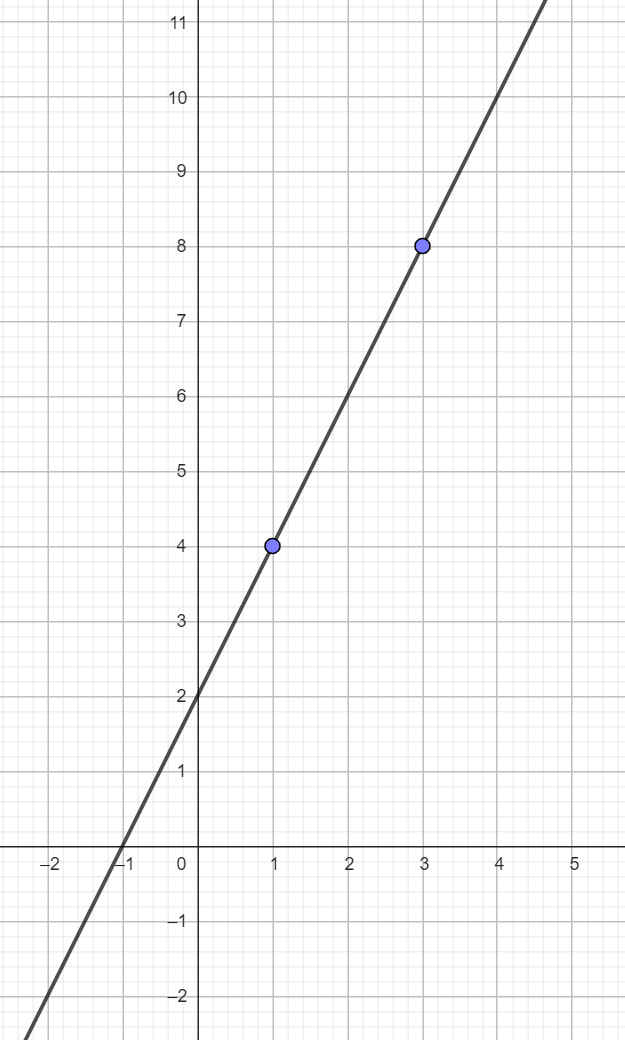
Es decir, nuestra función lineal es 
El gasto en la cantidad  de insumos de la empresa A se calcula usando la función:
de insumos de la empresa A se calcula usando la función: 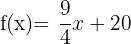 En cambio, la empresa B gasta sus insumos según la función:
En cambio, la empresa B gasta sus insumos según la función: 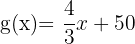 ¿En cuál de las empresas el crecimiento del gasto es más "lento"?
¿En cuál de las empresas el crecimiento del gasto es más "lento"?
Notemos que la pendiente de la función de la empresa A es 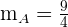 y la pendiente de la empresa B es
y la pendiente de la empresa B es 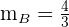 , es decir
, es decir 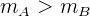
Ahora bien , si graficamos estas dos funciones obtendremos lo siguiente
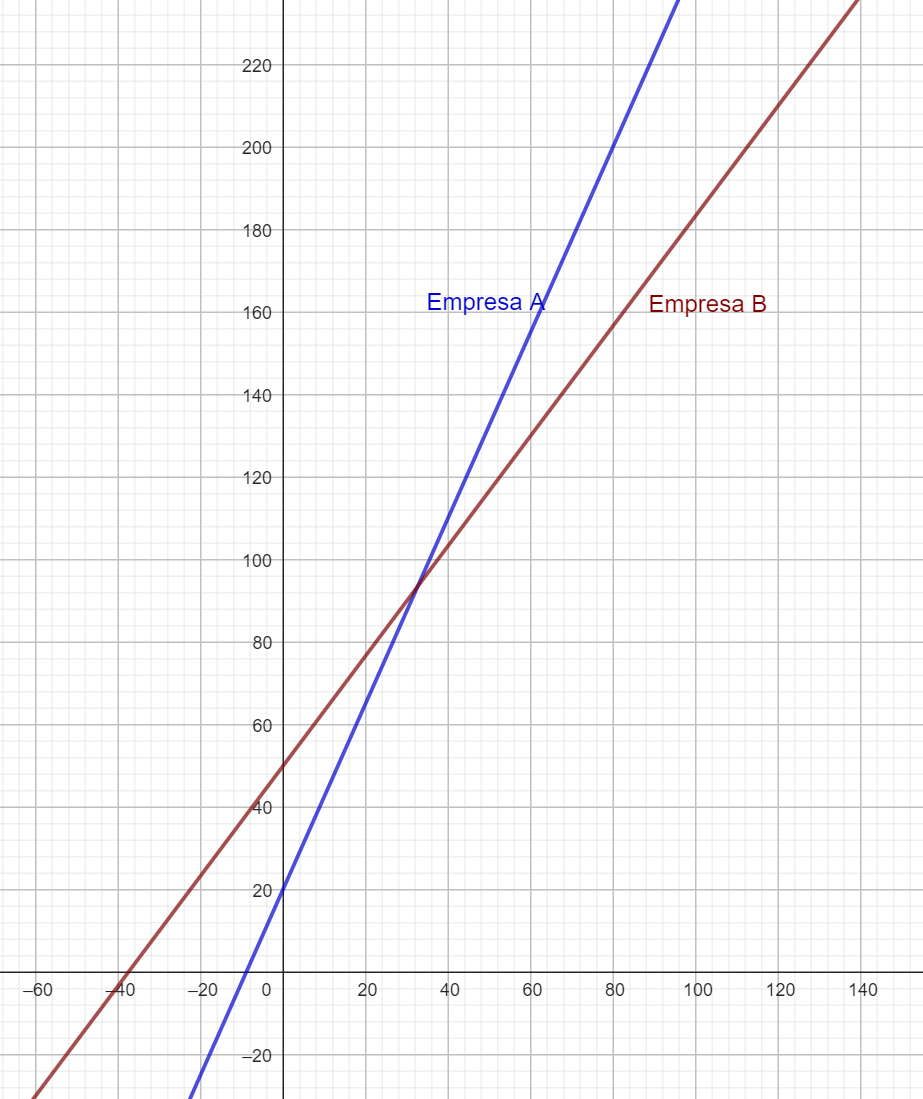
De aquí podemos ver que la empresa B tiene un crecimiento más "lento" de sus gastos. Además, notemos que este resultado también se verifica analizando las pendientes, ya que 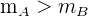 , por tanto, podemos decir que la función
, por tanto, podemos decir que la función  "crece" más rápido que la función
"crece" más rápido que la función  .
.
Cierta empresa de telefonía tiene la siguiente promoción "Por 40 dólares puedes hacer llamadas hasta por 300 minutos, luego por cada minuto adicional paga 0.50 dólares." Si Juliana optó por esa promoción, ¿Cuánto debe pagar por hablar 450 minutos?
Primero obtengamos una expresión algebraica de la función lineal que modela a la situación.
Sea  la cantidad de minutos adicionales que se realizan y no olvidemos considerar el monto fijo de 40 dólares por los primeros 300 minutos.
la cantidad de minutos adicionales que se realizan y no olvidemos considerar el monto fijo de 40 dólares por los primeros 300 minutos.
Considerando lo anterior obtenemos la siguiente función lineal que 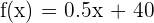
En este caso Juliana utilizo 450 minutos, es decir, se paso con 150 minutos y los que le corresponde pagar seria 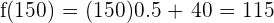 es decir, pagaría 115 dólares.
es decir, pagaría 115 dólares.
Hallar la ecuación de la recta que pasa por el punto 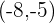 y de pendiente
y de pendiente 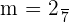
Recordemos la ecuación de la recta de la forma "punto - pendiente", es decir, esta formada con uno de los puntos de la recta y su pendiente, esta tiene la siguiente forma 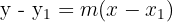 donde,
donde,  es el punto y
es el punto y  la pendiente.
la pendiente.
En este caso, sustituyendo obtendríamos 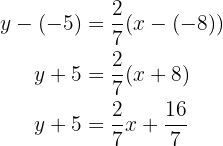
También podemos escribirla como 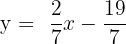
Resumir con IA:












Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.
Podrían mostrar los pares ordenados para graficarlo, gracias