Comprender una función matemática implica mucho más que simplemente evaluarla para distintos valores de entrada. Para tener una visión completa, es fundamental analizar tres aspectos clave: el dominio, el recorrido y su representación gráfica.
Dominio: Es el conjunto de todos los valores de entrada (valores de xx) para los cuales la función está definida. Determinar el dominio implica identificar restricciones como divisiones por cero o raíces de índice par de números negativos.
Recorrido (rango): Es el conjunto de valores que puede tomar la función como resultado (valores de yy). Encontrar el recorrido requiere comprender el comportamiento global de la función y, a menudo, se apoya en su gráfica o en métodos algebraicos.
Gráfica: Representar una función en el plano cartesiano permite visualizar de forma clara su comportamiento: crecimientos, decrecimientos, máximos, mínimos, simetrías y puntos notables.
En este artículo, se presentarán ejercicios resueltos paso a paso que te ayudarán a identificar el dominio y el recorrido de diversas funciones, así como a trazar sus gráficas de forma razonada. Este análisis es esencial para profundizar en temas más avanzados del cálculo y para aplicar funciones en contextos reales.
Ejercicios propuestos
Resolver los siguientes ejercicios realizando lo que se indica en cada caso:
Hallar el dominio y el recorrido de las siguientes funciones definidas a trozos, y además representarlas gráficamente.
a 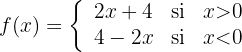
b 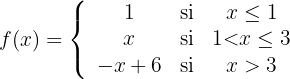
c 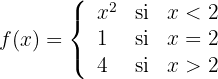
a Comencemos con la gráfica de la función (notemos que en cero no esta definida)

A partir de la gráfica podemos notar que
Dominio: 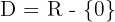
Recorrido: 
b Gráfica:
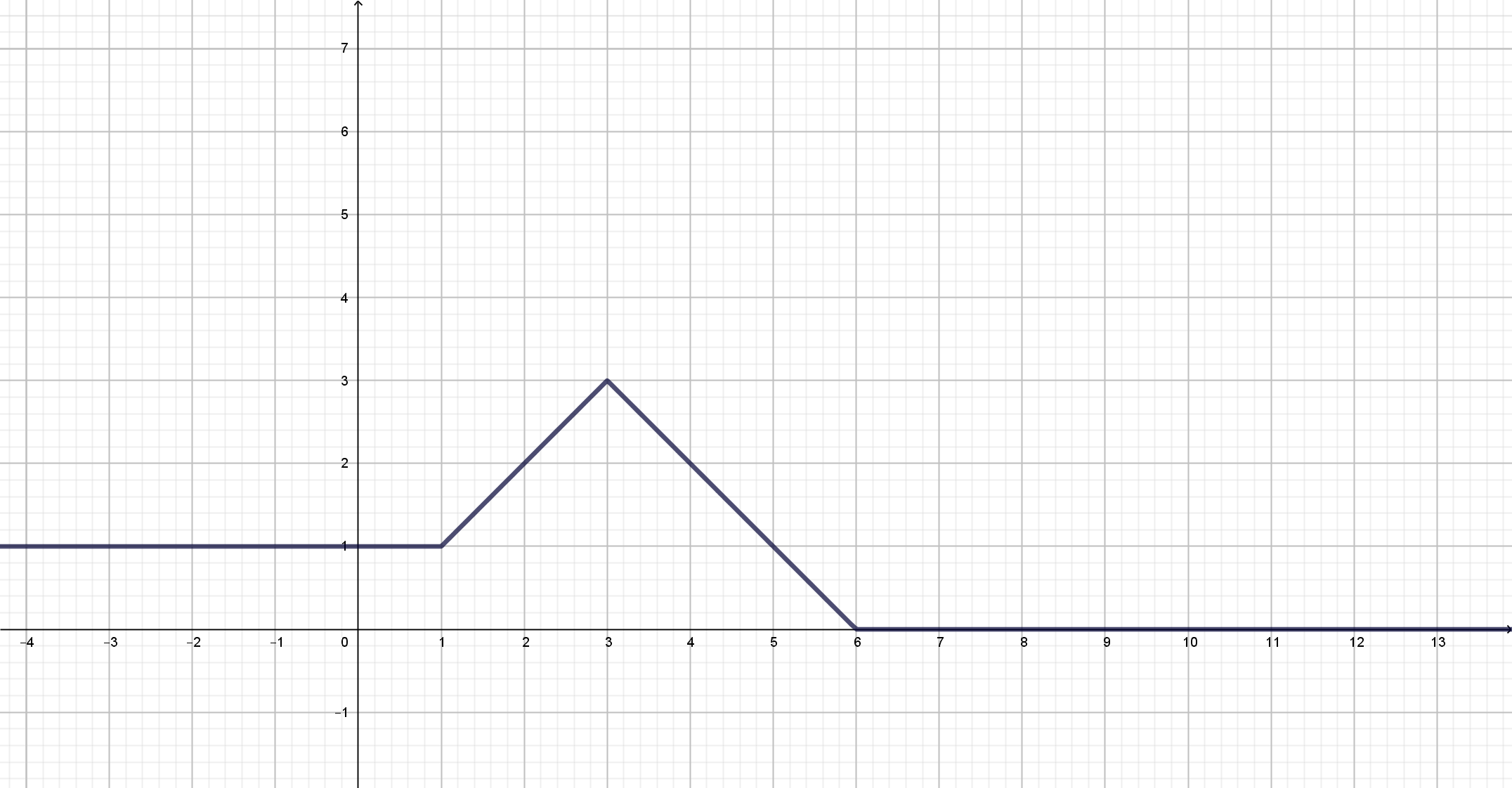
Notemos que
Dominio: 
Recorrido: 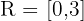
c Observemos que la gráfica esta definida en todos los reales pero no es continua
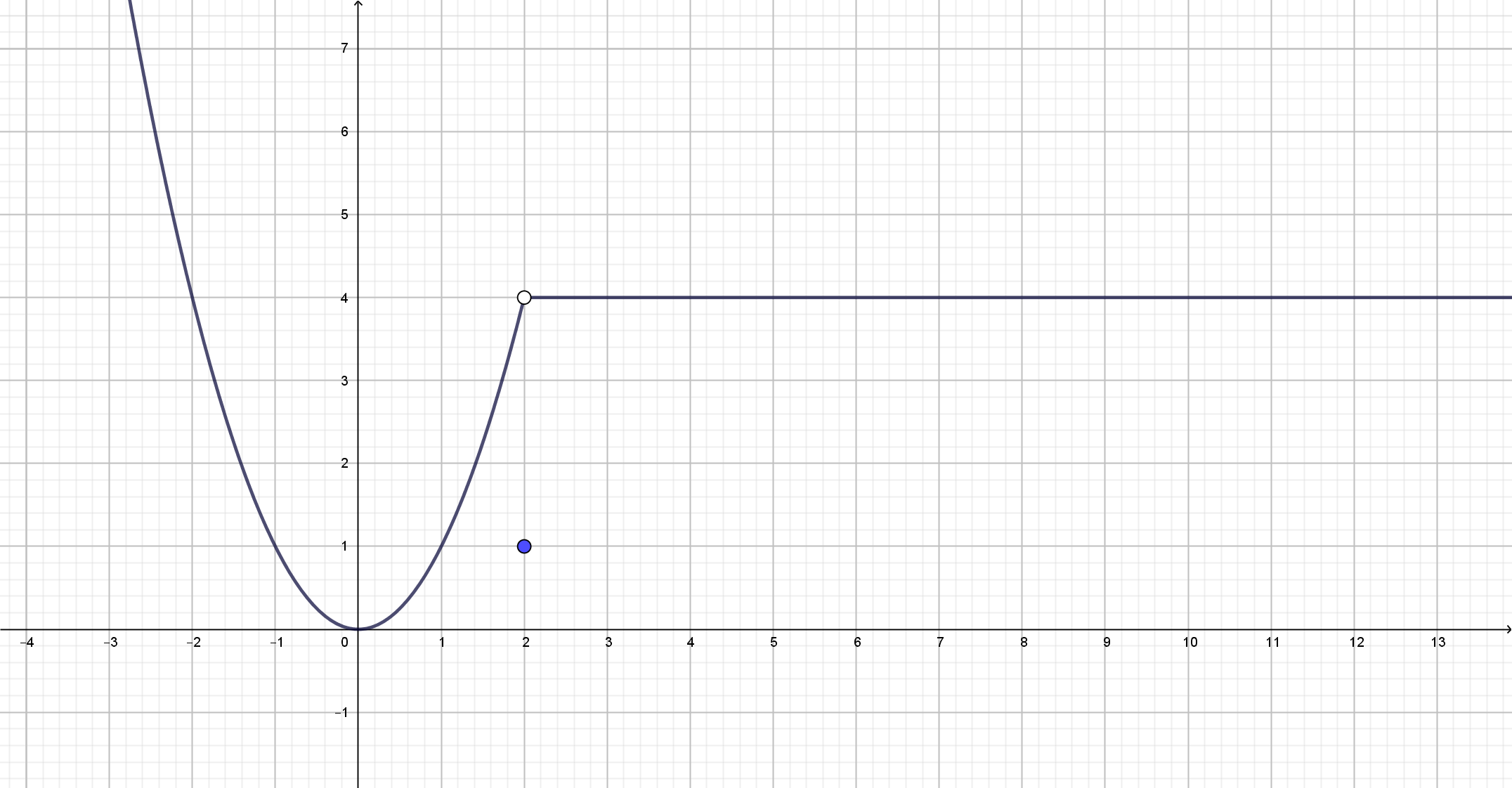
Y de la gráfica
Dominio: 
Recorrido: 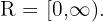
Hallar el dominio, el recorrido y representar gráficamente las siguientes funciones en valor absoluto:
a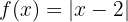
b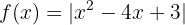
c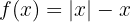
a 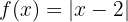 :
:
Se iguala a cero la función sin el valor absoluto, y se calculan sus raíces.
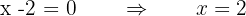
Se forman intervalos con las raíces y se evalúa el signo de cada intervalo
Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la  es negativa se cambia el signo de la función
es negativa se cambia el signo de la función
Recorrido : 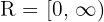
b 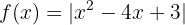
Se iguala a cero la función sin el valor absoluto y se calculan sus raíces.
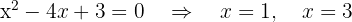
Se forman intervalos con las raíces y se evalúa el signo de cada intervalo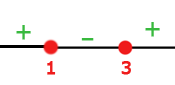
Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la  es negativa se cambia el signo de la función
es negativa se cambia el signo de la función
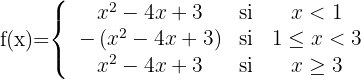
Representamos la función resultante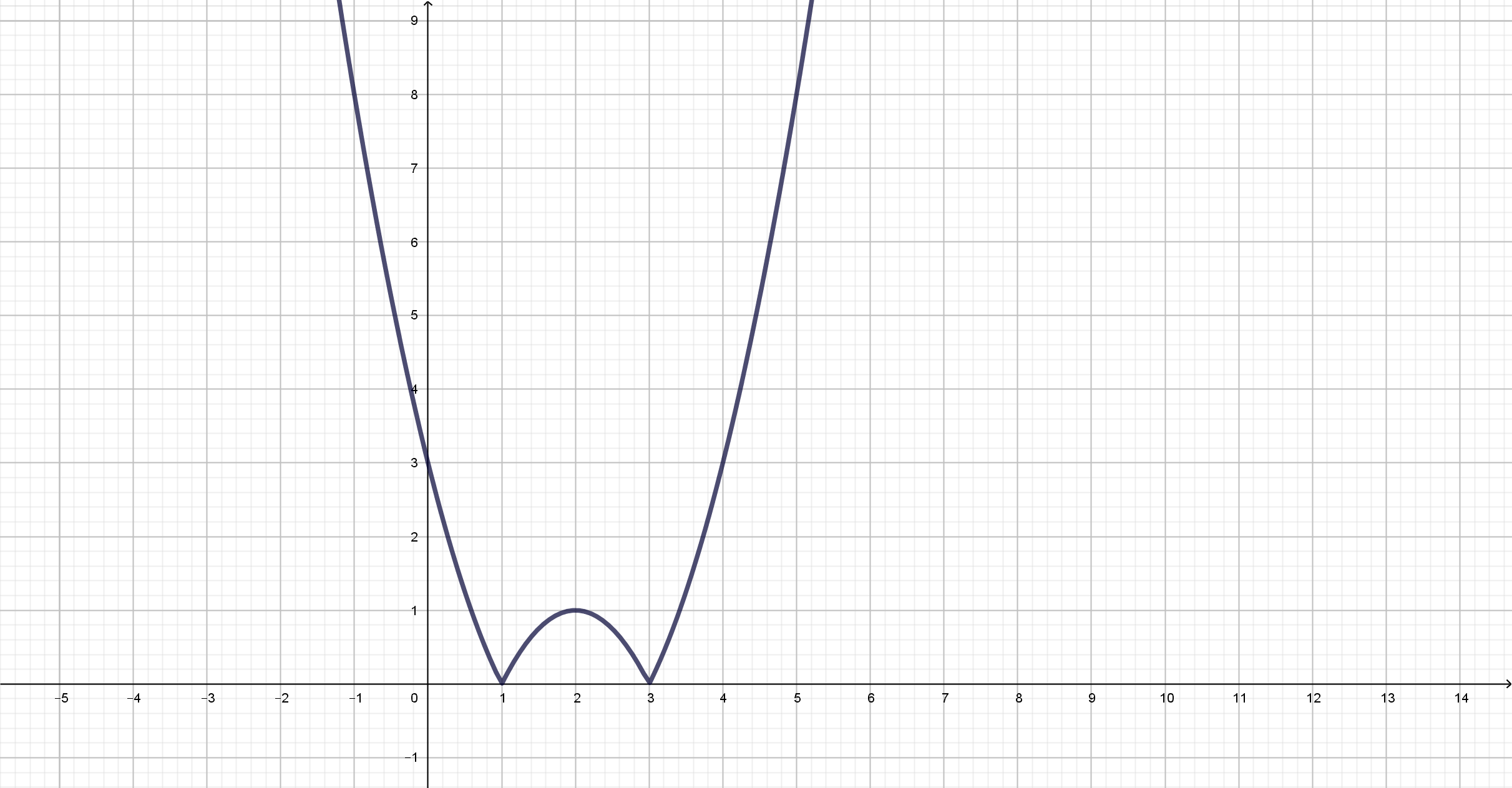
Por lo tanto

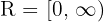
c 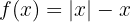
Se iguala a cero la función sin el valor absoluto, y se calculan sus raíces.

Se forman intervalos con las raíces y se evalúa el signo de cada intervalo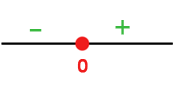
Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la  es negativa se cambia el signo de la función
es negativa se cambia el signo de la función
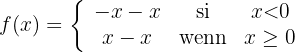
es decir
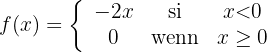
La gráfica de la función resultante es
Entonces

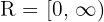
Representa gráficamente las funciones de la parte entera de  :
:
a 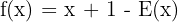
b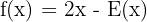
a 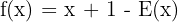
Primero tabulemos un par de puntos y después realicemos la gráfica
 |  |
|---|---|
| 0 | 1 |
| 0.5 | 1.5 |
| 0.9 | 1.9 |
| 1 | 1 |
| 1.5 | 1.5 |
| 1.9 | 1.9 |
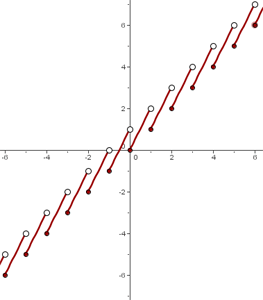
Gráfica:

b 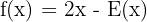
Representa las funciones racionales y determina su centro
a 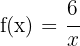
b 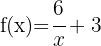
c 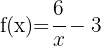
d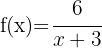
e 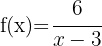
f 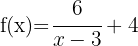
g 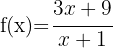
a 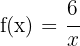
Hipérbola con gráfica

Y el centro de la hipérbola es:(0, 0)
b 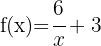
Notemos que 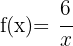 se desplaza 3 unidades hacia arriba, entonces
se desplaza 3 unidades hacia arriba, entonces
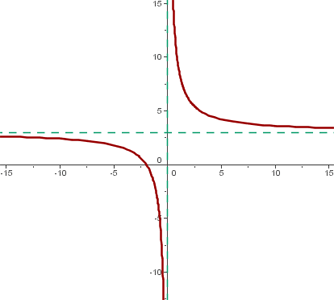
Por lo tanto el centro de la hipérbola es: (0, 3)
c 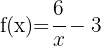
En este caso 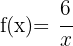 se desplaza 3 unidades hacia abajo, entonces
se desplaza 3 unidades hacia abajo, entonces
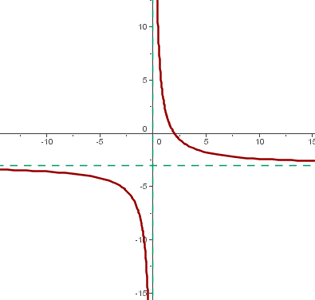
Entonces, el centro de la hipérbola es: (0, -3)
d 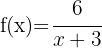
En este caso 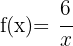 se desplaza 3 unidades hacia la izquierda
se desplaza 3 unidades hacia la izquierda
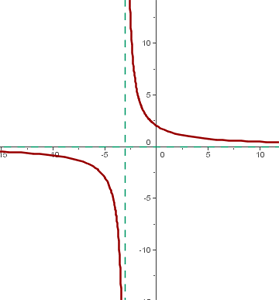
El centro de la hipérbola es: (−3, 0)
e 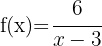
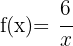 se desplaza 3 unidades hacia la derecha, entonces
se desplaza 3 unidades hacia la derecha, entonces

El centro de la hipérbola es: (3, 0)
f 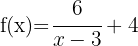
Tenemos que 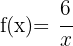 se desplaza hacia la derecha 3 unidades y4 hacia arriba
se desplaza hacia la derecha 3 unidades y4 hacia arriba
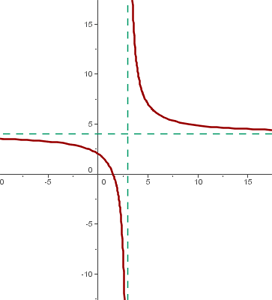
El centro de la hipérbola es: (3, 4)
g 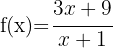
Notemos que
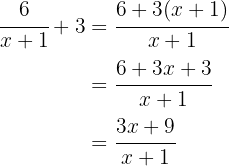
Es decir,
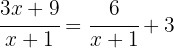 ,
,
y de aquí es mas sencillo ver que 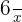 se desplaza hacia la izquierda 1 unidad y 3 unidades hacia arriba.
se desplaza hacia la izquierda 1 unidad y 3 unidades hacia arriba.
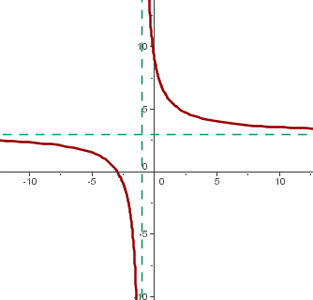
El centro de la hipérbola es: (−1, 3)
Representa las funciones exponenciales:
a 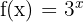
b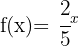
a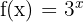
Notemos que
 |  |
|---|---|
| -3 | 1/27 |
| -2; | 1/9 |
| -1 | 1/3 |
| 0 | 1 |
| 1 | 3 |
| 2 | 9 |
| 3 | 27 |
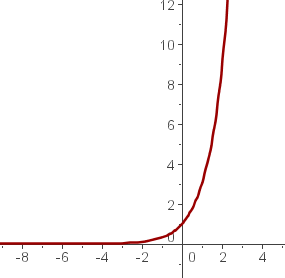
b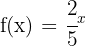
Notemos que
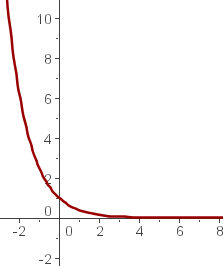
pues al tabular tenemos algo así
|  |
|---|---|
| −3 | 15.625 |
| −2 | 6.25 |
| −1 | 2.5 |
| 0 | 1 |
| 1 | 0.4 |
| 2 | 0.16 |
| 3 | 0.064 |
Representa las funciones exponenciales:
a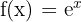
b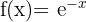
a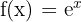
Notemos que
 |  |
|---|---|
| -3 | 1/27 |
| -2; | 1/9 |
| -1 | 1/3 |
| 0 | 1 |
| 1 | 3 |
| 2 | 9 |
| 3 | 27 |
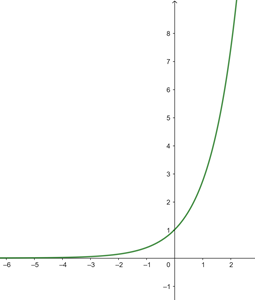
b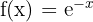
Notemos que
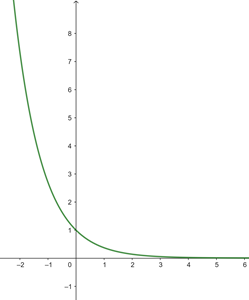
pues al tabular tenemos algo así
 |  |
|---|---|
| −3 | 15,625 |
| −2 | 6,25 |
| −1 | 2,5 |
| 0 | 1 |
| 1 | 0,4 |
| 2 | 0,16 |
| 3 | 0,064 |
Representa las funciones logarítmicas:
a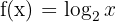
b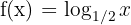
a 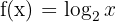
Tabulamos unos puntos para ver el comportamiento
 |  |
|---|---|
| 1/8 | -3 |
| 1/4 | -2 |
| 1/2 | -1 |
| 1 | 0 |
| 2; | 1 |
| 4 | 2 |
| 8 | 3 |
Su representación gráfica quedaría
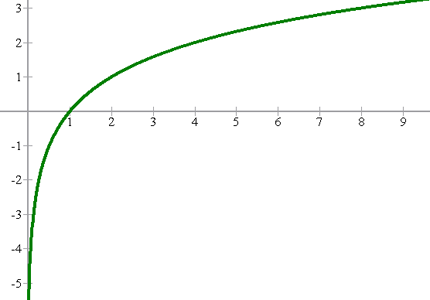
b 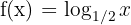
La gráfica que obtenemos es
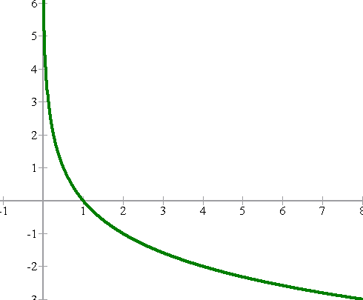
Al igual que en el ejercicio anterior se podría tabular para ver su comportamiento.
Representa las funciones logarítmicas:
a
b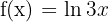
a 
Tabulamos unos puntos para ver el comportamiento
 |  |
|---|---|
| 1/8 | -3 |
| 1/4 | -2 |
| 1/2 | -1 |
| 1 | 0 |
| 2; | 1 |
| 4 | 2 |
| 8 | 3 |
Su representación gráfica quedaría
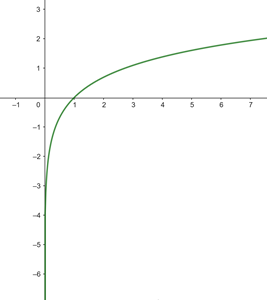
b 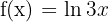
La gráfica que obtenemos es
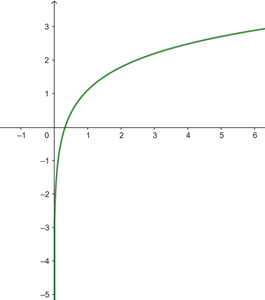
Al igual que en el ejercicio anterior se podría tabular para ver su comportamiento.
Representa las funciones trigonométricas:
a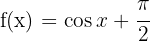
b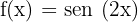
a 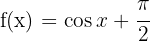
| 0 | 0 |
|---|---|
| π/4 | -0.7 |
| π/2 | -1 |
| 3π/4 | -0.7 |
| π | 0 |
| 5π/4 | 0.7 |
| 3π/2 | 1 |
| 7π/4 | 0.7; |
| 2π | 0 |
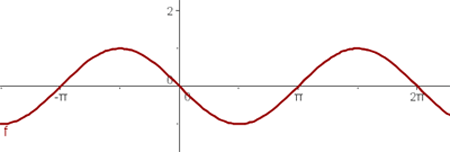
b 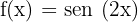
| 0 | 0 |
|---|---|
| π/4 | 1 |
| π/2 | 0 |
| 3π/4 | -1 |
| π | 0 |
| 5π/4 | 1 |
| 3π/2 | 0 |
| 7π/4 | -1 |
| 2π | 0 |
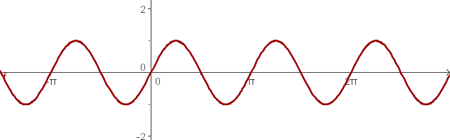
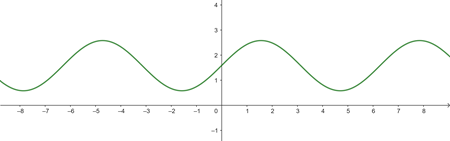
Representa las funciones trigonométricas:
a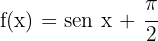
b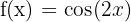
a 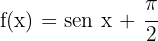
| 0 | 0 |
|---|---|
| π/4 | -0.7 |
| π/2 | -1 |
| 3π/4 | -0.7 |
| π | 0 |
| 5π/4 | 0.7 |
| 3π/2 | 1 |
| 7π/4 | 0.7; |
| 2π | 0 |
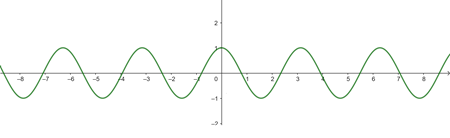
b 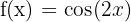
| 0 | 0 |
|---|---|
| π/4 | 1 |
| π/2 | 0 |
| 3π/4 | -1 |
| π | 0 |
| 5π/4 | 1 |
| 3π/2 | 0 |
| 7π/4 | -1 |
| 2π | 0 |
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Felicitaciones, muy interesantes los problemas y sobretodo las gráficas. ¿Pueden indicarme que programa utilizan?
Hola te agradecemos tu comentario, si te refieres a graficar te recomendamos geogebra, symbolat y otros mas.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.