Capítulos
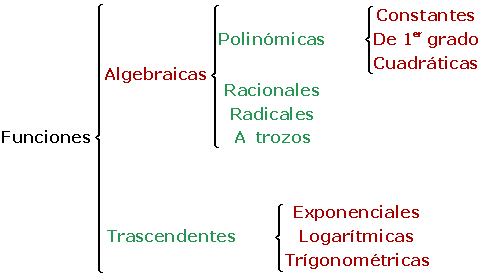

Funciones constantes
Son de la forma
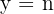
donde:
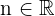 .
.
La pendiente es  .
.
La gráfica es una recta horizontal paralela a al eje de abscisas.
Funciones de primer grado
Función lineal
Es de la forma

donde:
 es la pendiente, que es la inclinación de la recta con respecto al eje de abscisas.
es la pendiente, que es la inclinación de la recta con respecto al eje de abscisas.
Su gráfica es una línea recta que pasa por el origen de coordenadas..
Función identidad
Es de la forma

donde:
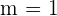 .
.
Su gráfica es la bisectriz del primer y tercer cuadrante.
Función afín
Es de la forma

donde:
 es la pendiente, que es la inclinación de la recta con respecto al eje de abscisas.
es la pendiente, que es la inclinación de la recta con respecto al eje de abscisas.
 es la ordenada en el origen y nos indica el punto de corte de la recta con el eje de ordenadas.
es la ordenada en el origen y nos indica el punto de corte de la recta con el eje de ordenadas.
Rectas verticales
Son del tipo:
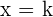
Las rectas paralelas al eje de ordenadas no son funciones, ya que un valor de  tiene infinitas imágenes y para que sea función sólo puede tener una.
tiene infinitas imágenes y para que sea función sólo puede tener una.
Función cuadrática
Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.
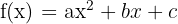
Para representar graficamente una parábola se requiere conocer los siguiente:
Vértice
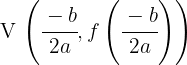
Por este punto pasa el eje de simetría de la parábola.
La ecuación del eje de simetría es:
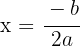
Puntos de corte con el eje 
En el eje de abscisas la segunda coordenada es cero, por lo que tendremos:
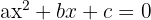
Resolviendo la ecuación podemos obtener:
1 Dos puntos de corte: 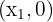 y
y 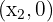 si
si 
2 Un punto de corte: 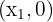 si
si 
3 Ningún punto de corte si 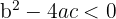
Punto de corte con el eje 
En el eje de ordenadas la primera coordenada es cero, por lo que tendremos:
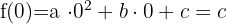
Así, el punto de corte es 
Funciones racionales
El criterio viene dado por un cociente entre polinomios:
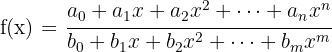
El dominio lo forman todos los números reales excepto los valores de  que anulan el denominador.
que anulan el denominador.
Dentro de este tipo tenemos las funciones de proporcionalidad inversa de ecuación:
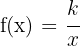 .
.
Funciones radicales
El criterio viene dado por la variable  bajo el signo radical.
bajo el signo radical.
Funciones definidas a trozos
Son funciones definidas por distintos criterios, según los intervalos que se consideren.
Funciones en valor absoluto
Las funciones en valor absoluto se transforman en funciones a trozos, sigiendo los siguientes pasos:
1 Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.
2 Se forman intervalos con las raíces y se evalúa el signo de cada intervalo.
3 Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la  es negativa se cambia el signo de la función.
es negativa se cambia el signo de la función.
4 Representamos la función resultante.
Función exponencial
Sea  un número real positivo. La función que a cada número real
un número real positivo. La función que a cada número real  le hace corresponder la potencia
le hace corresponder la potencia 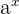 se llama función exponencial de base
se llama función exponencial de base  y exponente
y exponente  .
.
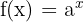
Funciones logarítmicas
La función logarítmica en base  es la función inversa de la exponencial en base
es la función inversa de la exponencial en base  .
.
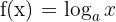
Funciones trigonométricas
Función seno

Función coseno
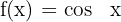
Función tangente

Función cotangente

Función secante
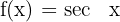
Función cosecante
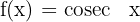
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.
Podrían mostrar los pares ordenados para graficarlo, gracias