En este artículo veremos ciertas características de las funciones trigonométricas, como sus graficas, sus dominios, continuidad, etc.
Seno
Empezaremos con la función seno
esta función tiene la siguiente grafica:
Notemos que esta función está bien definida para todo número real, por lo tanto su dominio son los números reales 
. Esto nos quiere decir que
Ahora, el conjunto imagen (o simplemente imagen o recorrido) de una función es el conjunto de valores que toma la función después de aplicarse sobre todos los elementos del dominio. En este caso, si vemos la imagen, es claro que la imagen es el intervalo cerrado 
, por lo tanto
Otra caracteristica importante de la función seno es que es periódica, esto es, existe un número real 
tal que
en este caso el periodo es 
radianes.
De la gráfica también se nota que la función es continua para todo 
, esto ya que no importa por donde nos acerquemos a un punto sobre la grafica, si es por la izquierda o derecha, siempre llegamos al mismo punto
Por último, debemos notar que la función es impar, esto es, para todo se cumple que
Así, en resumen tenemos lo siguiente:
1 Dominio: .
2 Imagen: .
3 Periodo: .
4 Continua: En todo su dominio .
5 Función impar.
Coseno
Analicemos la función coseno
esta función tiene la siguiente grafica:
Notemos que esta función está bien definida para todo número real, por lo tanto su dominio son los números reales . Esto nos quiere decir que
Ahora, el conjunto imagen (o simplemente imagen o recorrido) de una función es el conjunto de valores que toma la función después de aplicarse sobre todos los elementos del dominio. En este caso, si vemos la imagen, es claro que la imagen es el intervalo cerrado , por lo tanto
Otra caracteristica importante de la función coseno es que es periódica, esto es, existe un número real tal que
en este caso el periodo es radianes.
De la gráfica también se nota que la función es continua para todo , esto ya que no importa por donde nos acerquemos a un punto sobre la grafica, si es por la izquierda o derecha, siempre llegamos al mismo punto.
Por último, debemos notar que la función es par, esto es, para todo se cumple que
Así, en resumen tenemos lo siguiente:
1 Dominio: .
2 Imagen: .
3 Periodo: .
4 Continua: En todo su dominio .
5 Función par.
Tangente
Analicemos la función tangente
esta función tiene la siguiente grafica:
Notemos que esta función está bien definida para casi todo número real. Analicemos porque no está definida en todo número real. Recordemos que la función tangente se define como
Dado que la división entre cero no está definida, la función tangente no está definida cuanto 
, y esto ocurre para todo 
de la forma
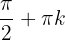en donde 
es entero. Así, el dominio de la tangente es
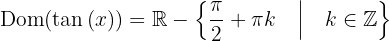
Ahora, el conjunto imagen (o simplemente imagen o recorrido) de una función es el conjunto de valores que toma la función después de aplicarse sobre todos los elementos del dominio. En este caso, si vemos la imagen, es claro que la imagen es todo el conjunto de los reales, esto es , por lo tanto
Otra caracteristica importante de la función tangente es que es periódica, esto es, existe un número real tal que
en este caso el periodo es 
radianes.
De la gráfica también se nota que la función es continua para todo 
, esto ya que no importa por donde nos acerquemos a un punto sobre la grafica, si es por la izquierda o derecha, siempre llegamos al mismo punto.
Por último, debemos notar que la función es impar, esto es, para todo se cumple que
Así, en resumen tenemos lo siguiente:
1 Dominio: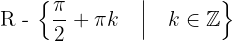 
.
2 Imagen: .
3 Periodo: .
4 Continua: En todo su dominio, pero no en todo .
5 Función impar.
Cosecante
Analicemosla función cosecante
esta función tiene la siguiente grafica:
Notemos que esta función está bien definida para caso todo número real, para entender por qué no está definida sobre todo recordemos que la función cosecante es el recíproco de la función seno, esto es
Dado que la división entre cero no está bien definida, la cosecante no está definida para los valores de en los cuales el seno es igual a cero; estos valores son 
, en donde es entero. Por lo tanto, el dominio de la cosecante es
Ahora, el conjunto imagen (o simplemente imagen o recorrido) de una función es el conjunto de valores que toma la función después de aplicarse sobre todos los elementos del dominio. En este caso, primero recordemos que la imagen del seno es . Tomaremos dos casos, primero cuando la imagen de seno está en 
y otro cuando la imagen del seno está en 
.
Empecemos con , es claro que
Ahora con , es claro que
Por lo tanto, la imagen de la cosecante es la unión de las imágenes de estos dos casos
Otra caracteristica importante de la función cosecante es que es periódica, esto es, existe un número real tal que
en este caso el periodo es radianes.
De la gráfica también se nota que la función es continua para todo , esto ya que no importa por donde nos acerquemos a un punto sobre la grafica, si es por la izquierda o derecha, siempre llegamos al mismo punto.
Por último, debemos notar que la función es impar, esto es, para todo se cumple que
Así, en resumen tenemos lo siguiente:
1 Dominio: 
.
2 Imagen: 
.
3 Periodo: .
4 Continua: En todo su dominio, pero no en todo .
5 Función impar.
Secante
Analicemosla función secante
esta función tiene la siguiente grafica:
Notemos que esta función está bien definida para caso todo número real, para entender por qué no está definida sobre todo recordemos que la función secante es el recíproco de la función coseno, esto es
Dado que la división entre cero no está bien definida, la secante no está definida para los valores de en los cuales el coseno es igual a cero; estos valores son 
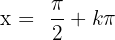, en donde es entero. Por lo tanto, el dominio de la secante es
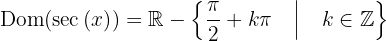
Ahora, el conjunto imagen (o simplemente imagen o recorrido) de una función es el conjunto de valores que toma la función después de aplicarse sobre todos los elementos del dominio. En este caso, primero recordemos que la imagen del coseno es . Tomaremos dos casos, primero cuando la imagen de coseno está en y otro cuando la imagen del coseno está en .
Empecemos con , es claro que
Ahora con , es claro que
Por lo tanto, la imagen de la secante es la unión de las imágenes de estos dos casos
Otra caracteristica importante de la función secante es que es periódica, esto es, existe un número real tal que
en este caso el periodo es radianes.
De la gráfica también se nota que la función es continua para todo , esto ya que no importa por donde nos acerquemos a un punto sobre la grafica, si es por la izquierda o derecha, siempre llegamos al mismo punto.
Por último, debemos notar que la función es par, esto es, para todo se cumple que
Así, en resumen tenemos lo siguiente:
1 Dominio: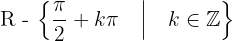 
.
2 Imagen: .
3 Periodo: .
4 Continua: En todo su dominio, pero no en todo .
5 Función par.
Cotangente
Analicemosla función cotangente
esta función tiene la siguiente grafica:
Notemos que esta función está bien definida para caso todo número real, para entender por qué no está definida sobre todo recordemos que la función cotangente está definida como
Dado que la división entre cero no está bien definida, la cotangente no está definida para los valores de en los cuales el seno es igual a cero; estos valores son , en donde es entero. Por lo tanto, el dominio de la cotangente es
Ahora, el conjunto imagen (o simplemente imagen o recorrido) de una función es el conjunto de valores que toma la función después de aplicarse sobre todos los elementos del dominio. En este caso es claro que, al igual que con la tangente, la imagen son todos los números reales, esto es
Otra caracteristica importante de la función cotangente es que es periódica, esto es, existe un número real tal que
en este caso el periodo es radianes.
De la gráfica también se nota que la función es continua para todo , esto ya que no importa por donde nos acerquemos a un punto sobre la grafica, si es por la izquierda o derecha, siempre llegamos al mismo punto.
Por último, debemos notar que la función es impar, esto es, para todo se cumple que
Así, en resumen tenemos lo siguiente:
1 Dominio: .
2 Imagen: .
3 Periodo: .
4 Continua: En todo su dominio, pero no en todo .
5 Función impar.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
El Punto de inflexión en el ejercicio 2: f(x) = x^3 + x + 1 debe ser (0, 1)
Hola agradecemos tu comentario, tenias razón era un error que ya se corrigió.
la grafica esta mal echa de signos de cada cuadrante
Hola te agradecemos por visitar nuestra pagina, podrías mencionar el número de ejercicio para poder rectificar esos errores que mencionas.
Se podría añadir un poco más de explicación a por que se hace cada paso ( ejemplo porque se divide todo por x ^2?)
Hola agradecemos que puedas darnos tu opinión, cuando surja una duda en este espacio de los comentarios estaremos atentos para darte una explicación con respecto a algo que no entiendas, exista un error o se pueda mejorar una explicación, solo comunícalo y te contestaremos.