¡Bienvenidos a nuestra página dedicada a explorar el área de las gráficas y funciones matemáticas. Las gráficas y funciones son la esencia misma de las matemáticas y desempeñan un papel fundamental en una amplia variedad de disciplinas, desde la física hasta la economía, pasando por la informática y la ingeniería.
En esta ocasión, te presentamos una serie de ejercicos prácticos en los cuales descubriremos cómo representar visualmente datos y relaciones matemáticas, cómo resolver problemas de la vida cotidiana utilizando funciones lineales y más.
Sin más que decir ¡comencemos a trazar el camino hacia el éxito en problemas de gráficas y funciones!
Representa las siguientes rectas:
a
b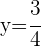
c
d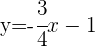
a
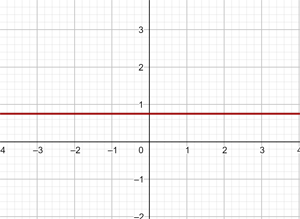
Es una función constante
b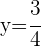
Es una función constante
c
Es una función lineal
 | |
|---|---|
| 0 | 0 |
| 1 | 2 |
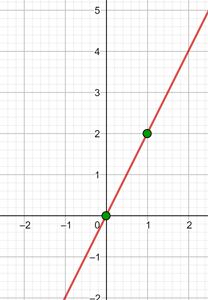
d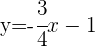
Es una función afín
| |
|---|---|
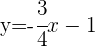| 0 | -1 |
| 4 | -4 |
Un grifo, que gotea, llena una probeta dejando caer cada minuto 
cm³ de agua. Forma una tabla de valores de la función, tiempo-capacidad de agua. Representa la función y encuentra la ecuación
La función que representa la relación tiempo-capacidad de agua es
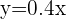
| Tiempo | Capacidad |
|---|---|
| 0 | 0 |
| 1 | 4 |
| 2 | 8 |
| 3 | 12 |
| 4 | 16 |
| ... | ... |
La gráfica de la función esta dada en la siguiente imagen.
Por el alquiler de un coche cobran 
€ diarios más 
€ por kilómetro. Encuentra la ecuación de la recta que relaciona el coste diario con el número de kilómetros y represéntala. Si en un día se ha hecho un total de 
km, ¿qué importe debemos abonar?
El importe que debemos abonar esta determinado por la siguiente función.
Donde representa el número de kilómetros, entonces al reemplazar en la ecuación anterior tenemos que el valor exacto que debemos abonar es
= 
€
Finalmente su gráfica esta representada por
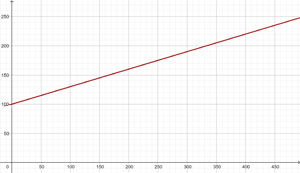
La siguiente función proporciona la distancia (en kilómetros) que recorre una moto a una velocidad de km/h en función del tiempo t (en horas):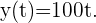 
¿Qué distancia recorre en 
horas? ¿Y en 
horas?
La gráfica que representa la función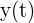 
es la de una recta que pasa por el origen con pendiente .
Para hallar los valores debemos calcular la imagen de y de :
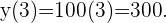
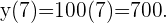
Por lo tanto en horas recorre kilómetros y en horas recorre 
kilómetros
Consideremos la siguiente ecuación de una recta 
. Escribir la ecuación de una recta paralela que pase por el punto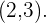 
La pendiente de una recta es el coeficiente que acompaña a la variable . Para obtener un recta paralela debemos obtener la misma pendiente que la recta inicial.
La gráfica de la función es la de una recta que pasa por el punto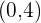 
y que tiene pendiente 
.
De esta forma todas las rectas paralelas a la recta inicial tienen ecuación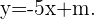
Solo debemos hallar el valor de 
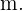Para esto solo reemplazamos los valores de y 
de punto indicado 
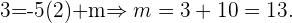
Por lo tanto la ecuación de la recta que buscamos esta dada por
La compañía de agua de Santiago tiene los siguientes precios, le cobra 
€ mensuales de cuota y 
€ por cada metro cúbico. Calcular la función que proporciona el costo de la factura mensual de Santiago en función de los metros cúbicos que consume
Si Santiago consume un total de metros cúbicos de agua el costo total será
Además de esto, hay que sumar € de la cuota.
Por tanto, la función es
La gráfica de esta función es la de una recta que pasa por el punto 
y que tiene pendiente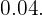 
La siguiente función representa el número de camisetas que vende por día una tienda de ropa
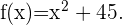
¿Cuántas camisetas se venden en días? ¿Y en 
días? ¿Y en 
días?
La gráfica de la función esta dada por la gráfica de una parábola centrado en el eje de las ordenadas y con punto de inflexión en 
.
La siguiente tabla nos muestran los valores que necesitamos de la función y que indican el número de camisetas.
| (número de días) |  |
|---|---|
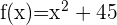| 3 | 54 |
| 5 | 70 |
| 35 | 1270 |
Sara está planeando un viaje por carretera desde la Ciudad A hasta la Ciudad B. Quiere hacer un seguimiento de la distancia que recorre cada día y crear un gráfico para visualizar su progreso. Sara tiene un mapa que muestra la distancia entre varias ciudades a lo largo del camino. Las distancias entre las ciudades son las siguientes:
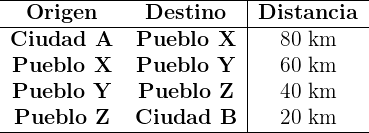
Sara planea viajar desde la Ciudad A hasta el Pueblo X el primer día, desde el Pueblo X hasta el Pueblo Y el segundo día, desde el Pueblo Y hasta el Pueblo Z el tercer día y desde el Pueblo Z hasta la Ciudad B el cuarto día.
a Crea un gráfico que represente el viaje por carretera de Sara, con la distancia recorrida en el eje vertical y los días del viaje en el eje horizontal. Etiqueta los días como Día 1, Día 2, Día 3 y Día 4. Marca las distancias recorridas en cada día utilizando las distancias proporcionadas entre las ciudades.
b ¿Qué ecuación lineal pasa por estos puntos?
a La primer coordenada de nuestros puntos corresponde a el día y la segunda coordenada corresponde a la distancia recorrida en ese día. Así, el gráfico es
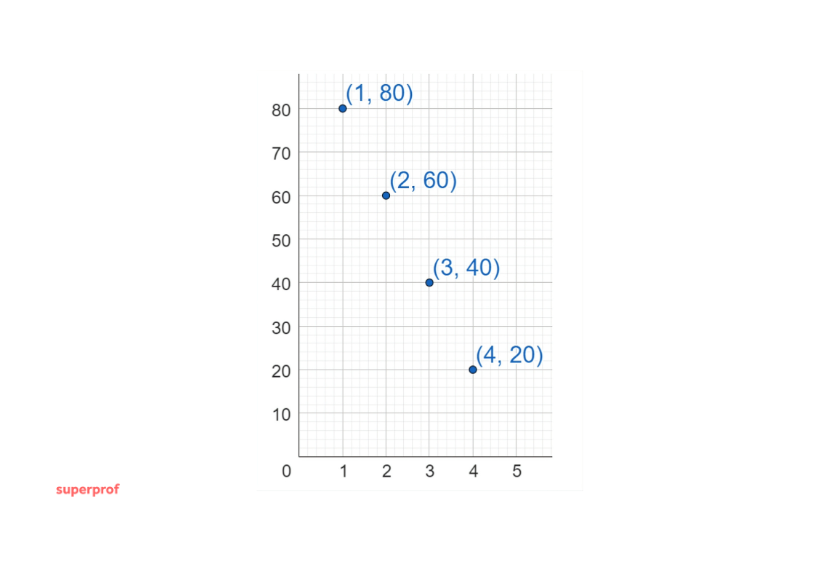
b Recordemos que, si tenemos dos puntos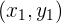 
y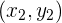 
, la recta que pasa por estos puntos está dada por
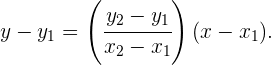
En este caso, tomamos los puntos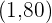 
y 
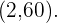Así,
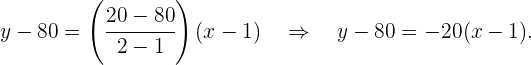
Por lo tanto, la ecuación de la recta buscada es
La ganancia de una empresa local ha modelado sus ventas en miles de euros con la ecuación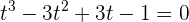 
en el intervalo 
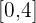, donde cada intervalo unitario representa una cuarta parte del año.
a ¿En qué valores de 
se registró una venta de 0 euros?
b Después del primer cuarto del año, ¿la empresa tiende a aumentar o disminuir sus ventas?
a La ecuación es equivalente a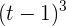 
, por lo que solamente en en 
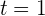la empresa registra una venta de 0 euros.
b Aumentar, ya que para todo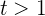 
, se cumple que 
Un autor popular aclama haber escrito un libro completo en 
horas. En la primera hora, escribió 
palabras por minuto, y en la segunda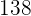 
palabras por minuto, de manera ininterrumpida.
a En la primera hora, ¿cuántas palabras ha escrito?
b) Al termino de la segunda hora, ¿cuántas palabras ha escrito?
a La primera hora se puede representar mediante la ecuación 
, donde 
representa los minutos.
Entonces, después de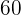 
minutos, se han escrito
.
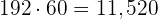b Al inicio de la segunda hora, el autor redujo su velocidad de escritura, por lo que ahora se representa por medio de la ecuación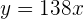 
, donde nuevamente representa los minutos.
Entonces, solamente en la segunda hora, ha escrito
.
Por lo que, en total, ha escrito
palabras.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
El Punto de inflexión en el ejercicio 2: f(x) = x^3 + x + 1 debe ser (0, 1)
Hola agradecemos tu comentario, tenias razón era un error que ya se corrigió.
la grafica esta mal echa de signos de cada cuadrante
Hola te agradecemos por visitar nuestra pagina, podrías mencionar el número de ejercicio para poder rectificar esos errores que mencionas.
Se podría añadir un poco más de explicación a por que se hace cada paso ( ejemplo porque se divide todo por x ^2?)
Hola agradecemos que puedas darnos tu opinión, cuando surja una duda en este espacio de los comentarios estaremos atentos para darte una explicación con respecto a algo que no entiendas, exista un error o se pueda mejorar una explicación, solo comunícalo y te contestaremos.