Representa las siguientes rectas
1y = 2
2y = −2
3y = x
4y = 2x − 1
5y = −2x − 1
6y = ½x − 1
1 y = 2
Es una función constante
Trazamos una recta paralela al eje de abscisas que pase por (0, 2)
2 y = −2
Es una función constante
Trazamos una recta paralela al eje de abscisas que pase por (0, –2)
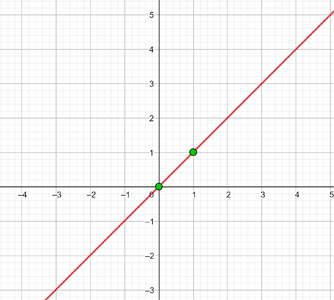
3y = x
Es la función identidad
| x | y = x |
|---|---|
| 0 | 0 |
| 1 | 1 |
4y = 2x − 1
Es una función afín, generamos a dos puntos para hacer la recta
| x | y = 2x −1 |
|---|---|
| 0 | −1 |
| 1 | 1 |
5y = −2x − 1
Es una función afín
| x | y = −2x −1 |
|---|---|
| 0 | −1 |
| 1 | −3 |
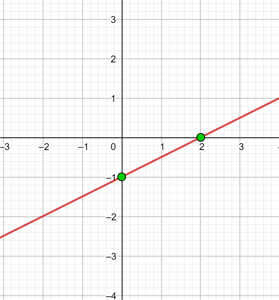
6y = ½x − 1
Es una función afín
| x | y = ½x − 1 |
|---|---|
| 0 | −1 |
| 2 | 0 |
Representa las siguientes funciones
Sabiendo que:
1Tiene pendiente −3 y ordenada en el origen −1.
2Tiene por pendiente 4 y pasa por el punto (−3, 2).
1 Tiene pendiente −3 y ordenada en el origen −1.
Se trata de una función afín que es del tipo y = mx + n
La pendiente es: m = –3
La ordenada en el origen es: n = –1
la función a representar es:
y = −3x −1
| x | y = −3x − 1 |
|---|---|
| 0 | −1 |
| 1 | −4 |
2Tiene por pendiente 4 y pasa por el punto (−3, 2).
Se trata de una función afín que es del tipo y = mx + n
La pendiente es: m = 4
Para hallar n sustitimos el punto en la función y = 4x + n
2 = 4 · (−3) + n llegando a que n = 14
La función es:
y = 4x + 14
| x | y = 4x +14 |
|---|---|
| 0 | 14 |
| 1 | 18 |
Problema de función con boquerones
Tres kilogramos de boquerones valen 18 €. Escribe y representa la función que define el coste de los boquerones en función de los kilogramos comprados.
Tres kilogramos de boquerones valen 18 €. Escribe y representa la función que define el coste de los boquerones en función de los kilogramos comprados.
Se trata de una función lineal: y = mx, donde
- x representa los kilogramos
- m el costo por kilogramo
- y el costo total
Según el ejercicio tenemos que y=18, x=3 así que debemos encontrar m
Sustituimos los valores de la variable independiente y la dependiente
18 = m · 3 al despejar llegamos a m = 6
Significa que la función es:
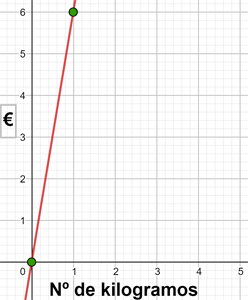
y = 6x
| x | y = 6x |
|---|---|
| 0 | 0 |
| 1 | 6 |
Problema de función afín
En las semanas de cultivo de una planta, que medía 2 cm, se ha observado que su crecimiento es directamente proporcional al tiempo, viendo que en una semana ha pasado a medir de 2 cm a 2.5 cm.
Establecer una función afín que dé la altura de la planta en función del tiempo y representar gráficamente.
En las semanas de cultivo de una planta, que medía 2 cm, se ha observado que su crecimiento es directamente proporcional al tiempo, viendo que en una semana ha pasado a medir de 2 cm a 2.5 cm.
Altura inicial = 2 cm
Crecimiento semanal = 2.5 − 2 = 0.5 cm
Entonces, si x representa el número de semanas entonces 0.5x será el incremento en altura que se llevará a cabo en las x semanas, sin embargo al principio de la observación ya media 2 cm, por lo tanto la función será:
y = 0.5x + 2
cuya gráfica es
Problema de funciones de temperatura y profundidad
Cuando se excava hacia el interior de la tierra, la temperatura aumenta con arreglo a la siguiente fórmula:
t = 15 + 0.01 h.
donde t es la temperatura alcanzada en grados centígrados y h es la profundidad, en metros, desde la corteza terrestre.
Calcular:
1¿Qué temperatura se alcanza a los 100 m de profundidad? 2¿Cuántos metros hay que excavar para alcanzar una temperatura de 100 ºC?
1¿Qué temperatura se alcanza a los 100 m de profundidad?
Nos piden la variable dependiente
t = 15 + 0.01 · 100 = 16 ºC
2¿Cuántos metros hay que excavar para alcanzar una temperatura de 100 ºC?
Nos piden la variable independiente
100 = 15 + 0.01h
0.01h = 100 – 15
0.01h=85
Problema sobre el nivel de contaminación de una ciudad
El nivel de contaminación de una ciudad a las 6 de la mañana es de 30 partes por millón y crece de forma lineal 25 partes por millón cada hora. Sea y la contaminación en el instante t después de las 6 de la mañana.
1Hallar la ecuación que relaciona y con t.
2Calcular el nivel de contaminación a las 4 de la tarde.
El nivel de contaminación de una ciudad a las 6 de la mañana es de 30 partes por millón y crece de forma lineal 25 partes por millón cada hora. Sea y la contaminación en el instante t después de las 6 de la mañana.
1 Hallar la ecuación que relaciona y con t.
y = 30 + 25t
2Calcular el nivel de contaminación a las 4 de la tarde.
Desde las 6 de la mañana a las cuatro de la tarde han transcurrido 10 horas.
f(10) = 30 + 25 · 10 = 280
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
El Punto de inflexión en el ejercicio 2: f(x) = x^3 + x + 1 debe ser (0, 1)
Hola agradecemos tu comentario, tenias razón era un error que ya se corrigió.
la grafica esta mal echa de signos de cada cuadrante
Hola te agradecemos por visitar nuestra pagina, podrías mencionar el número de ejercicio para poder rectificar esos errores que mencionas.
Se podría añadir un poco más de explicación a por que se hace cada paso ( ejemplo porque se divide todo por x ^2?)
Hola agradecemos que puedas darnos tu opinión, cuando surja una duda en este espacio de los comentarios estaremos atentos para darte una explicación con respecto a algo que no entiendas, exista un error o se pueda mejorar una explicación, solo comunícalo y te contestaremos.