Ejemplos de problemas de optimización y su resolución.
De todos los triángulos isósceles de 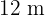 de perímetro, hallar los lados del que tome área máxima.
de perímetro, hallar los lados del que tome área máxima. 
Tenemos que optimizar (maximizar) el área del triángulo, es decir, la función definida por su área. Ya que el triángulo es isósceles, su base es el lado 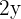 , los lados iguales serán
, los lados iguales serán  y su altura la podemos calcular usando el teorema de Pitágoras,
y su altura la podemos calcular usando el teorema de Pitágoras,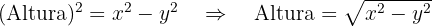 así obtenemos
así obtenemos
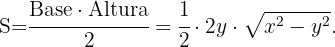
Con la condición de que el perímetro del triángulo mide 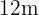 podemos relacionar las variables:
podemos relacionar las variables:
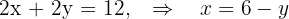
Este resultado lo podemos sustituir en la función:
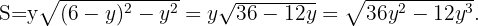
Para hallar los extremos locales, derivamos, igualamos a cero y calculamos las raíces:
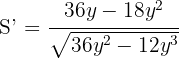
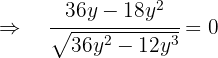
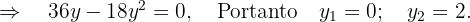
Recordemos que si la segunda derivada tiene signo negativo, entonces obtendremos un máximo local. Así realizamos la 2ª derivada y evaluamos en  , ya que la solución
, ya que la solución  no es factible.
no es factible.
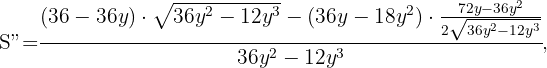
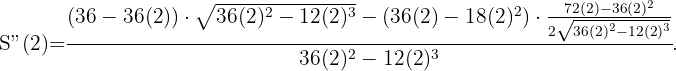
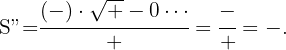
Por lo que queda probado que en  hay un máximo. La base
hay un máximo. La base 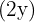 mide
mide  y los lados oblicuos
y los lados oblicuos 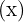 también miden
también miden 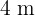 , por lo que el triangulo de área máxima sería un triangulo equilátero.
, por lo que el triangulo de área máxima sería un triangulo equilátero.
El valor de un diamante es proporcional al cuadrado de su peso. Divide un diamante de 2 g en dos partes de forma que la suma de los valores de los dos diamantes formados sea mínima.
Digamos que  es el peso de un diamante. Ya que el valor del diamante es proporcional al cuadrado del peso, entonces el valor de nuestro diamante debe estar dado por
es el peso de un diamante. Ya que el valor del diamante es proporcional al cuadrado del peso, entonces el valor de nuestro diamante debe estar dado por  , donde
, donde  es una constante positiva de proporcionalidad. Al dividir un diamante de
es una constante positiva de proporcionalidad. Al dividir un diamante de 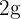 en dos partes de pesos
en dos partes de pesos  y
y  , tenemos una ecuación que nos relaciona sus valores,
, tenemos una ecuación que nos relaciona sus valores,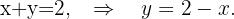
De esta forma los valores de cada una de las partes son,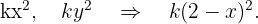
Y la función que deseamos optimizar es la dada por la suma de dichos valores,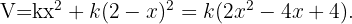
Para encontrar los valores extremos de esta función debemos derivar e igualar a cero,
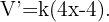

Como podemos ver hemos obtenido una solución  para nuestro problema. Para comprobar que esta solución nos da un mínimo valor, hallamos la segunda derivada y checamos que es positiva, en efecto,
para nuestro problema. Para comprobar que esta solución nos da un mínimo valor, hallamos la segunda derivada y checamos que es positiva, en efecto,
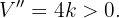
De esta forma el diamante se ha de dividir en dos partes iguales de 1 g.
Encontrar, de entre todas las rectas que pasan por por el punto  aquella que forma con la partes positivas de los ejes de coordenadas un triángulo de área mínima.
aquella que forma con la partes positivas de los ejes de coordenadas un triángulo de área mínima.
De la forma punto-pendiente de la recta tenemos que la ecuación de la recta que pasa por el punto 
es 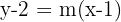
Puesto que queremos que los vértices queden en las partes positivas de los ejes coordenados necesitamos el valor que toma  cuando
cuando  y el valor que toma
y el valor que toma  cuando
cuando 
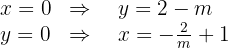
Por tanto 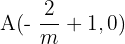 y
y 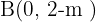 vértices del triangulo.
vértices del triangulo. 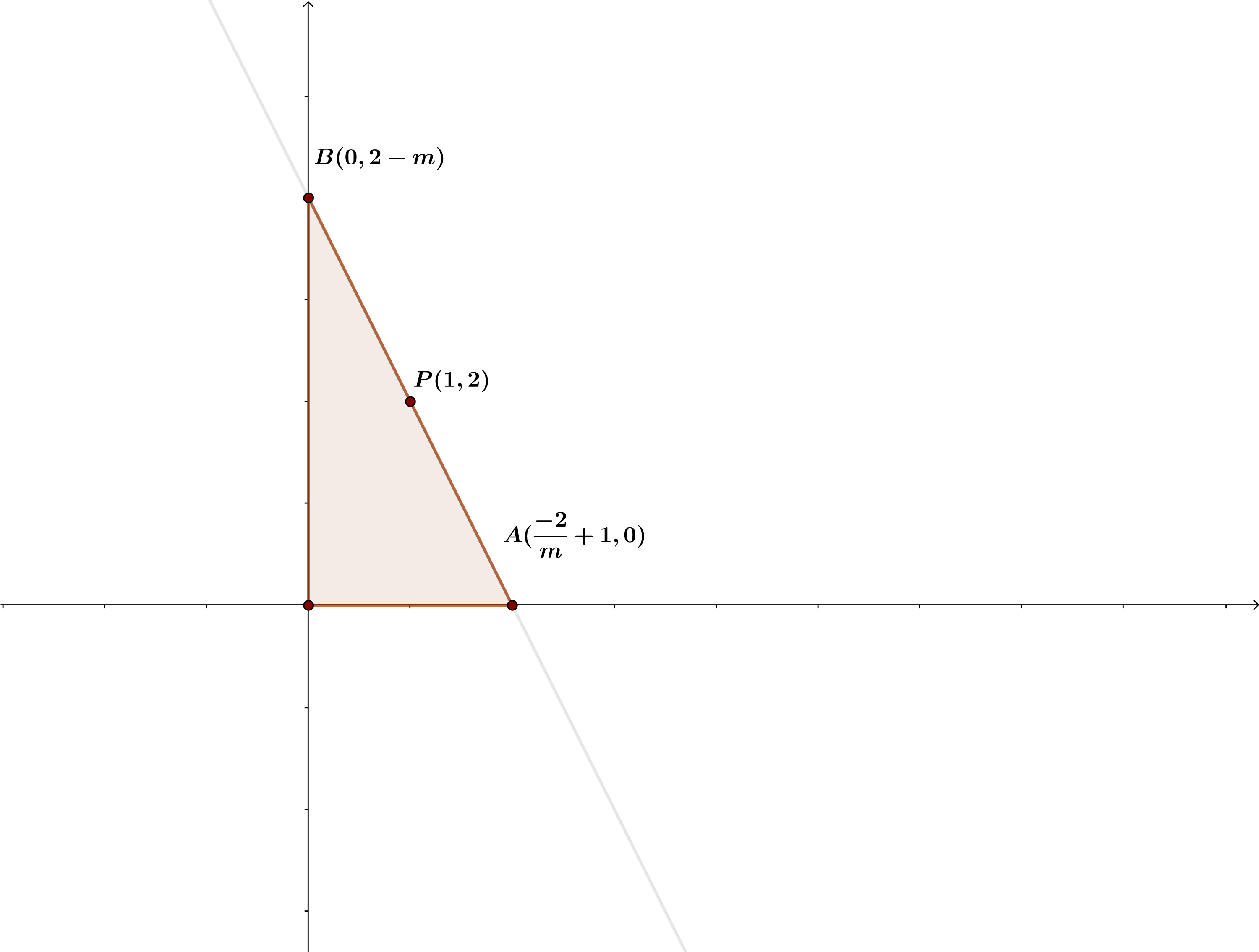
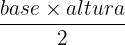
en este caso queda 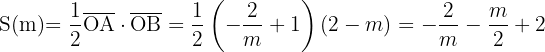
Calculamos la derivada e igualamos a cero para encontrar valores críticos: 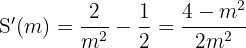
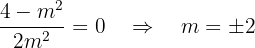
Notemos que con  no se formaría un triángulo porque las coordenadas de A y B coinciden con el origen de coordenadas, por tanto tomamos
no se formaría un triángulo porque las coordenadas de A y B coinciden con el origen de coordenadas, por tanto tomamos 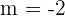
Calculamos la derivada segunda y sustituimos: 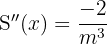
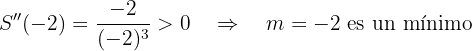
Por tanto, la recta es la que tiene pendiente 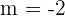
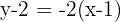
Una boya, formada por dos conos rectos de hierro unidos por sus bases ha de ser construido mediante dos placas circulares de  de radio. Calcular las dimensiones de la boya para que su volumen sea máximo.
de radio. Calcular las dimensiones de la boya para que su volumen sea máximo. 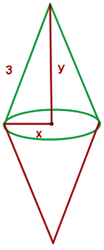
Recordemos que la formula del volumen del cono es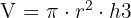
en este caso de acuerdo a la figura tendríamos que la función a optimizar es
Relacionamos las variables: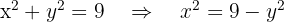
Sustituimos en la función:
Derivamos, igualamos a cero y calculamos las raíces.
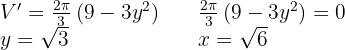
Realizamos la derivada segunda para comprobar el resultado obtenido
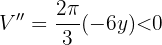
Obtener el triángulo isósceles de área máxima inscrito en un círculo de radio 12 cm.
¿Buscas un profesor de mates? ¡Encuéntralo en Superprof!
El área del triángulos esta dada por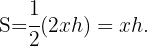
La figura nos muestra un triángulo rectángulo formado usando el radio del círculo, un lado del triángulo y su altura. Usando el teorema de Pitagoras se sigue que
Al remplazar en  tenemos que
tenemos que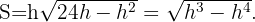
Como siempre el siguen paso es derivar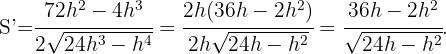 Al igualar a cero concluimos que,
Al igualar a cero concluimos que,
Con estos valores podemos decir lo siguiente sobre los valores del triángulo,
Base: ,
,
Lado: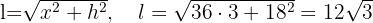
Para concluir o comprobar que estos valores nos dan un máximo para el área debemos evaluar la segunda derivada en 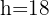 y obtener un valor negativo, en efecto,
y obtener un valor negativo, en efecto,

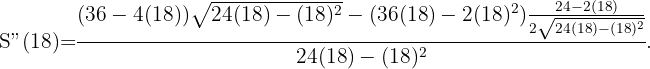
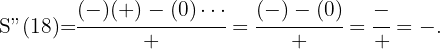
Un triángulo isósceles de perímetro  , gira alrededor de su altura engendrando un cono. ¿Qué valor debe darse a la base para que el volumen del cono sea máximo?
, gira alrededor de su altura engendrando un cono. ¿Qué valor debe darse a la base para que el volumen del cono sea máximo?
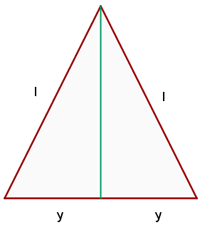
La función a optimizar es definida por el volumen del cono formado al rotar el triángulo,
Ya que el perímetro es  y el triángulo gira alrededor de su altura, de la figura obtenemos lo siguiente
y el triángulo gira alrededor de su altura, de la figura obtenemos lo siguiente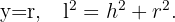
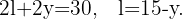
Al combinar estas ecuaciones se sigue que,
Ya que tenemos todas las variables en términos de  , podemos remplazar en la función volumen,
, podemos remplazar en la función volumen,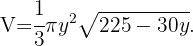
Lo siguiente es derivar,
Al igualar a cero obtenemos los siguientes valores para 

y para la base del triángulo; Base: 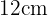 ,
,
Para comprobar que en 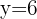 obtenemos un máximo, debemos evaluar la segunda derivada de
obtenemos un máximo, debemos evaluar la segunda derivada de  es este valor y obtener un valor negativo,
es este valor y obtener un valor negativo,
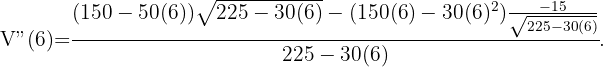

Si eres más de aprender desde casa, ¿por qué no optas por un profesor matematicas online?
Se pretende fabricar una lata de conserva cilíndrica (con tapa) de 1 litro de capacidad. ¿Cuáles deben ser sus dimensiones para que se utilice el mínimo posible de metal?
Lo que el problema nos pide es minimizar la función que define el área de la lata cilíndrica, la cual esta dada por
Puesto que la lata debe contener un litro entonces su volumen es igual a  , es decir,
, es decir,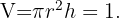
Despejando  , se sigue que
, se sigue que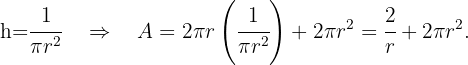
Derivamos la función 
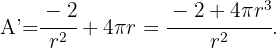
Para hallar los valores extremos igualamos la ecuación anterior a cero y despejamos el valor de 

Obtenemos el valor de  usando el valor de
usando el valor de  ,
,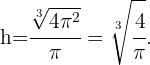
Al comprobar con el criterio de la segunda derivada tenemos que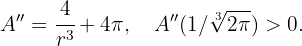
Por lo tanto las dimensiones de la lata son mínimas con 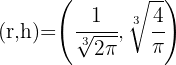 .
.
Descomponer el número 44 en dos sumandos tales que el quíntuplo del cuadrado del primero más el séxtuplo del cuadrado del segundo sea un mínimo.
Queremos descomponer el numero  en dos sumandos, entonces
en dos sumandos, entonces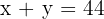
y queremos que el quíntuplo del cuadrado del primero más el séxtuplo del cuadrado del segundo sea un mínimo por tanto
Puesto que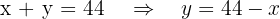
sustituimos " "
"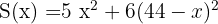
Derivando e igualando a cero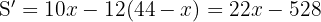

Calculando la segunda derivada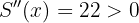
Por tanto mínimo y los números son
Se tiene un alambre de 1 m de longitud y se desea dividirlo en dos trozos para formar con uno de ellos un círculo y con el otro un cuadrado. Determinar la longitud que se ha de dar a cada uno de los trozos para que la suma de las áreas del círculo y del cuadrado sea mínima.
Si el cuadrado tiene lado  y el círculo tiene radio
y el círculo tiene radio  , entonces la función a optimizar es:
, entonces la función a optimizar es: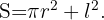
Ya que el alambre tiene una longitud de un  , entonces la suma de los perímetros del círculo y el cuadrado nos da la ecuación que relaciona las variables,
, entonces la suma de los perímetros del círculo y el cuadrado nos da la ecuación que relaciona las variables,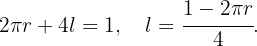
Remplazando en  se sigue,
se sigue,
El siguiente paso es derivar la función  e igualar a cero, para hallar los valor extremos,
e igualar a cero, para hallar los valor extremos,
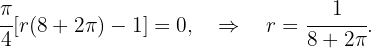
Con este valor para  podemos concluir queTrozo del círculo:
podemos concluir queTrozo del círculo: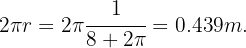 Trozo del cuadrado:
Trozo del cuadrado:

La parte final para este caso de minimizar, como siempre, en este tipo de problemas es encontrar la segunda derivada y checar que es positiva en los valores encontrados
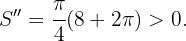
Hallar las dimensiones del mayor rectángulo inscrito en un triángulo isósceles que tiene por base  y por altura
y por altura  .
.
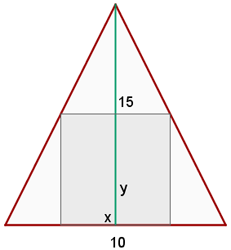
Tenemos que la función a optimizar es Relacionamos las variables: al tener dos triángulos semejantes se obtiene
Relacionamos las variables: al tener dos triángulos semejantes se obtiene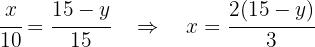
Sustituimos en la función: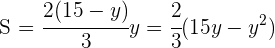
Derivamos, igualamos a cero y calculamos las raíces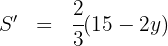 Igualamos a cero y calculamos las raíces
Igualamos a cero y calculamos las raíces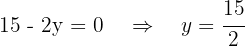
Por tanto, la base es 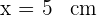 . Realizamos la derivada segunda para comprobar el resultado obtenido
. Realizamos la derivada segunda para comprobar el resultado obtenido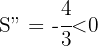
En conclusión, para 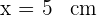 y
y  , existe un máximo relativo
, existe un máximo relativo
Recortando convenientemente en cada esquina de una lámina de cartón de dimensiones 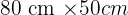 un cuadrado de lado
un cuadrado de lado  y doblando convenientemente (véase figura), se construye una caja. Calcular
y doblando convenientemente (véase figura), se construye una caja. Calcular  para que volumen de dicha caja sea máximo.
para que volumen de dicha caja sea máximo.
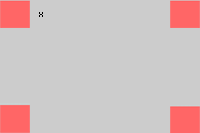
Primero debemos encontrar la función a optimizar. Esta función es definida por el volumen de la caja, la cual tiene como lados a  ,
,  y como altura a
y como altura a  , así nuestra función es
, así nuestra función es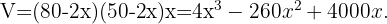
Notemos que en este problema solo interviene una variable, así que podemos pasar directamente a buscar los extremos locales. Recordemos que para esto debemos derivar nuestra función e igualar la ecuación resultante a cero.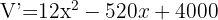
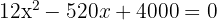
Esta ecuación la podemos resolver utilizando la fórmula general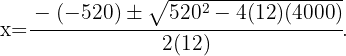
Lo cual nos da las siguientes dos soluciones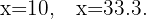
Notemos que la solución 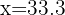 no es validad ya que tendríamos que el lado
no es validad ya que tendríamos que el lado  seria negativo. De esta forma nuestro único extremo local es
seria negativo. De esta forma nuestro único extremo local es 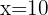 .Calculando la segunda derivada de la función
.Calculando la segunda derivada de la función 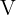 y evaluando en
y evaluando en 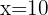 , obtenemos
, obtenemos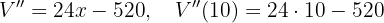
Una hoja de papel debe tener 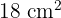 de texto impreso, márgenes superior e inferior de
de texto impreso, márgenes superior e inferior de 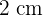 de altura y márgenes laterales de
de altura y márgenes laterales de 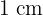 de anchura. Obtener razonadamente las dimensiones que minimizan la superficie del papel.
de anchura. Obtener razonadamente las dimensiones que minimizan la superficie del papel.

¿Buscas clases particulares matematicas? ¡Están en Superprof!
La función que debemos minimizar esta dada por el área de la superficie de papel,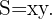
De las condiciones del problema debemos extraer ecuaciones que relacionen las variables. Ya que debemos tener 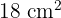 de texto impreso podemos decir que
de texto impreso podemos decir que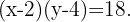
Despejando para  , se sigue que
, se sigue que 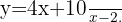 Al remplazar en la función
Al remplazar en la función  obtenemos
obtenemos
Ahora podemos derivar la función para encontrar los extremos locales
Igualamos la derivada a cero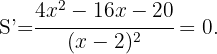
Esto significa que debemos resolver la ecuación 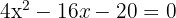 . Notemos que
. Notemos que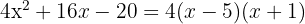
Por tanto nuestras soluciones son  y
y  . Debemos rechazar la solución
. Debemos rechazar la solución  pues es negativa. Por lo tanto tenemos una sola solución a nuestro problema.
pues es negativa. Por lo tanto tenemos una sola solución a nuestro problema.
Dado esto no tenemos necesidad de calcular la segunda derivada podemos concluir que en  y
y 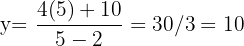 minimizan la superficie de papel.
minimizan la superficie de papel.
El beneficio neto mensual, en millones de euros, de una empresa que fabrica autobuses viene dado por la función: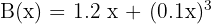 donde
donde  es el número de autobuses fabricados en un mes. Calcula la producción mensual que hacen máximo el beneficio.
es el número de autobuses fabricados en un mes. Calcula la producción mensual que hacen máximo el beneficio.
Derivamos la función del beneficio mensual e igualamos a cero
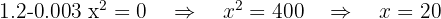
Calculamos la segunda derivada y sustituimos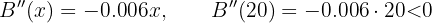
Por tanto máximo.
Una huerta tiene actualmente 25 árboles, que producen 600 frutos cada uno. Se calcula que por cada árbol adicional plantado, la producción de cada árbol disminuye en 15 frutos. Calcular:
1 La producción actual de la huerta.
2 La producción que se obtendría de cada árbol si se plantan x árboles más.
3 La producción a la que ascendería el total de la huerta si se plantan x árboles más.
4 ¿Cuál debe ser el número total de árboles que debe tener la huerta para qué la producción sea máxima?
¿Quieres encontrar clases particulares matematicas Zaragoza? ¡Hazlo con Superprof!
1 La producción actual de la huerta:Producción actual: 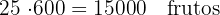
2 La producción que se obtendría de cada árbol si se plantan  árboles más:Si se plantan
árboles más:Si se plantan  árboles más, la producción de cada árbol será:
árboles más, la producción de cada árbol será:
3 La producción a la que ascendería el total de la huerta si se plantan  árboles más:
árboles más: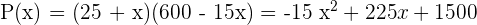
4 ¿Cuál debe ser el número total de árboles que debe tener la huerta para qué la producción sea máxima? Derivamos e igualamos a cero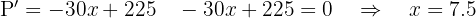 Puesto que la segunda derivada es negativa,
Puesto que la segunda derivada es negativa,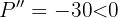 Entonces la produccion maxima sera con
Entonces la produccion maxima sera con 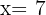 . La producción será máxima si la huerta tiene
. La producción será máxima si la huerta tiene
Un sector circular tiene un perímetro de 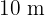 . Calcular El radio y la amplitud del sector de mayor área.
. Calcular El radio y la amplitud del sector de mayor área. 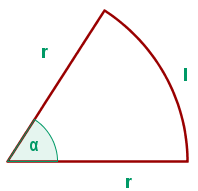
Nuestra función a optimizar es la definida por el área del sector circular, de la figura tenemos: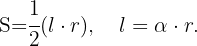
Ya que le perímetro es 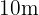 , entonces
, entonces
Al remplazar en la función  , se sigue que
, se sigue que
El siguiente paso es derivar la función  e igualar a cero para encontrar un valor extremo,
e igualar a cero para encontrar un valor extremo,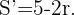
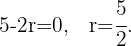
Después de obtener un valor para  podemos obtener valores para
podemos obtener valores para  y
y 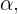

En este caso la segunda derivada de  es constante y negativa,
es constante y negativa,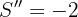 .
.
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Felicitaciones, muy interesantes los problemas y sobretodo las gráficas. ¿Pueden indicarme que programa utilizan?
Hola te agradecemos tu comentario, si te refieres a graficar te recomendamos geogebra, symbolat y otros mas.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.