Capítulos
- Dominio de la función polinómica entera
- Dominio de la función racional
- Dominio de la función radical de índice impar
- Dominio de la función radical de índice par
- Dominio de la función logarítmica
- Dominio de la función exponencial
- Dominio de la función seno
- Dominio de la función coseno
- Dominio de la función tangente
- Dominio de la función cotangente
- Dominio de la función secante
- Dominio de la función cosecante
- Dominio de operaciones con funciones
El dominio de una función está formado por todos los elementos que tienen imagen.
Es decir, son los valores de 
que podemos sustituir en la regla de correspondencia de una función para obtener el valor correspondiente de 
.
que significa que el dominio de una función son aquellos valores de que pertenecen a los números reales para los cuales existe un valor asociado de la función .
El subconjunto de los números reales en el que se define la función se llama dominio o campo existencia de la función.
Se designa por D.
La variable x perteneciente al dominio de la función recibe el nombre de variable independiente.
Conjunto inicial Conjunto final
Dominio Conjunto imagen o recorrido
Dominio de la función polinómica entera
El dominio de una función polinómica es 
, porque cualquier número real tiene imagen.
También son funciones polinómicas enteras las que tienen un número (una constante) en el denominador:
Ejemplos de dominios de las funciones polinómicas
1 
2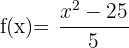 
Puedes probar que al sustituir cualquier valor de en las funciones siempre obtendrás un valor correspondiente para .
Dominio de la función racional
El dominio es menos los valores que anulan al denominador (no puede existir una fracción cuyo denominador sea cero)..
Ejemplo de ejercicio de dominio de la función racional
1 ¿Qual es el dominio de la función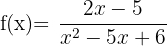 
?
Igualamos el denominador a 
y resolvemos la ecuación
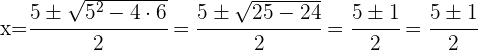
Dominio de la función radical de índice impar
El dominio es el dominio de la función radicando.
1
2
Dominio de la función radical de índice par
El dominio está formado por todos los valores del radicando que hacen que éste sea mayor o igual que cero.
1
2
3¿Cuál es el dominio de la función
?
En este caso, el denominador debe ser mayor que cero y, además, debemos buscar los valores de para que la raíz exista, por lo que:
4Determinar el dominio de la función 
.
El radicando tiene que ser mayor que cero y el denominador distinto de cero
5 Obtener el dominio de la función 
.
Como el radicando debe ser mayor o igual que cero, planteamos la desigualdad:
Resolvemos la inecuación de segundo grado
Las raíces de la ecuación de segundo grado asociada a la desigualdad son: 
y 
Por lo que los intervalos en los que se cumple la desigualdad serían:
El dominio lo forman los valores menores que el -2 y mayores que 7, incluyéndolos.
6 Obtener el dominio de la función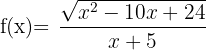 
.
En este caso se deben cumplir dos condiciones, una para el cociente y otra para la raíz, por lo que el numerador tiene que ser mayor o igual que cero y el denominador distinto de cero. Por lo que:
Dominio de la función logarítmica
El dominio está formado por todos los valores que hacen que la función que aparece dentro del logaritmo sea mayor que cero.
Se debe cumplir:
Dominio de la función exponencial
Ejemplos de dominio de funciones exponenciales
1 
2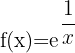 
El dominio es igual a menos los valores que anulan el denominador del exponente
3 
El dominio coincide con el campo de existencia real de la raíz
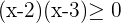
Dominio de la función seno
El dominio de la función seno es
Dominio de la función coseno
El dominio de la función coseno es
Dominio de la función tangente
Dominio de la función cotangente
Dominio de la función secante
Dominio de la función cosecante
Dominio de operaciones con funciones
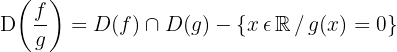
Recuerda que también puedes encontrar un profesor particular para cursos de matematicas adaptados a tu nivel.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
El Punto de inflexión en el ejercicio 2: f(x) = x^3 + x + 1 debe ser (0, 1)
Hola agradecemos tu comentario, tenias razón era un error que ya se corrigió.