Gráfica de una función
gráfica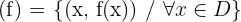 
Para representar una función estudiaremos los diferentes tipos de funciones y el dominio de cada una de ellas.
Cálculo del dominio de una función
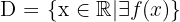
Dominio de la función polinómica
El dominio de una función polinómica es todo el eje real, es decir,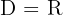 
.
Dominio de la función racional
Una función racional es de la forma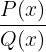 
, donde 
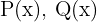son polinomios. El dominio es 
menos los valores que anulan al denominador, es decir, donde 
.
Dominio de la función radical de índice impar
Una función radical es de la forma 
, para el caso donde 
es impar, el dominio es .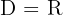
Dominio de la función radical de índice par
Una función radical es de la forma , para el caso donde es par, el dominio está formado por todos los valores que hacen que el radicando sea mayor o igual que cero, es decir, 
Dominio de la función logarítmica
Una función logarítmica es de la forma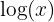 
. El dominio está formado por todos los valores que hacen que el radicando sea mayor que cero, es decir, .
Dominio de la función exponencial
La forma de una función exponencial es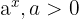 
donde 
es una constante, el dominio es .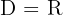
Dominio de la función seno
El dominio de la función seno es .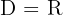
Dominio de la función coseno
El dominio de la función coseno es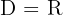
Dominio de la función tangente
El dominio de la función tangente es:
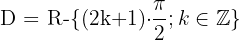
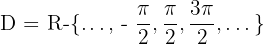
Dominio de la función cotangente
El dominio de la función cotangente es:
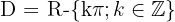
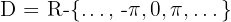
Dominio de la función secante
El dominio de la función secante es:
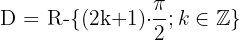
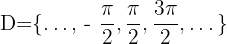
Dominio de la función cosecante
El dominio de la función cosecante es:
Dominio de operaciones con funciones
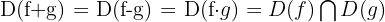
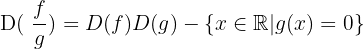
Simetría
Simetría respecto del eje de ordenadas
Función par
Para saber si una función es par se tiene que cumplir la siguiente condición: 
Ejemplo:
1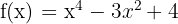
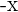, es decir,
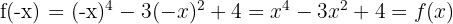,lo cual satisface la condición de paridad.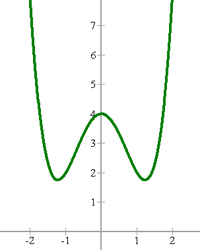
Por la gráfica anterior podemos ver la simetría con respecto al eje y.
Simetría respecto al origen
Función impar
Para saber si una función es par se tiene que cumplir la siguiente condición: 
Ejemplo:
1
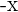, es decir,
,lo cual satisface la condición de que una función es impar.
Periodicidad
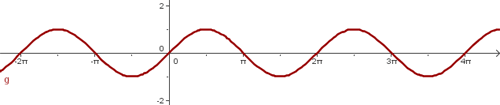
La función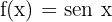 
es periódica de periodo 
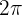, ya que cumple que:
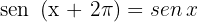
Si 
es periódica de período T, también lo es 
, y su período es 
.
Puntos de corte con los ejes
Puntos de corte con el eje OX
Para hallar los puntos de corte con el eje de abscisas hacemos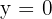 
y resolvemos la ecuación resultante.
Punto de corte con el ejes OY
Para hallar el punto de corte con el eje de ordenadas hacemos 
y calculamos el valor de 
.
Ejemplo de puntos de corte con los ejes
1Hallar los puntos de corte con los ejes de la función
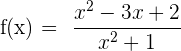
, entonces la ecuación a resolver es:
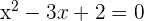
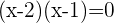
Entonces,
Los puntos de intersección con el eje x son 
.
Para los puntos de corte con el eje OY, hacemos 
, entonces:
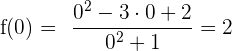
El punto de intersección con el eje Y es 
.
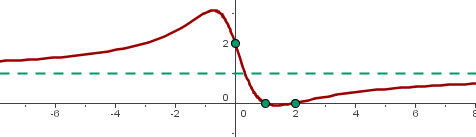
Asíntotas
Asíntotas horizontales
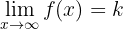
ó
dónde y = k
Asíntotas verticales
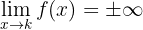
dónde x = k
Asíntotas oblicuas
Las asíntotas son de la forma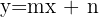 
, entonces
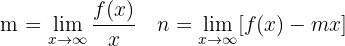
Ejemplo
1 Calcular las asíntotas de la función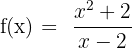 
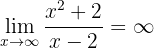Por lo tanto, no hay asíntotas horizontales. Asíntotas verticales
Aquí vemos que el límite a ocupar es,
Entonces la asíntota vértical es 
.
Asíntotas oblicuas
Resolvemos los respectivos límites para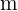 
y .
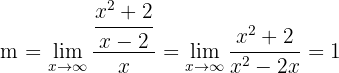
Entonces la asintota es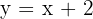 
Ramas parabólicas
Hay ramas parabólicas si:
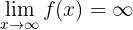
ó
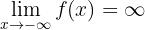
Rama parabólica en la dirección del eje OY
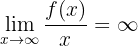
Rama parabólica en la dirección del eje OX
Crecimiento y decrecimiento
Para hallar el crecimiento y decrecimiento seguiremos los siguientes pasos:
1 Derivar la función:
2 Obtener las raíces de la derivada primera, para ello hacemos: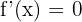 
.
3 Formamos intervalos abiertos con los ceros (raíces) de la derivada primera y los puntos de discontinuidad (si los hubiese)
4 Tomamos un valor de cada intervalo, y hallamos el signo que tiene en la derivada primera.
5 Escribimos los intervalos de crecimiento y decrecimiento.
Máximos y mínimos relativos
Para hallar los extremos relativos seguiremos los siguientes pasos:
1 Hallamos la derivada primera y calculamos sus raíces.
2 Realizamos la 2ª derivada, y calculamos el signo que toman en ella las raíces de derivada primera y si:
es un máximo relativo
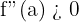es un mínimo relativo
3 Calculamos la imagen (en la función) de los extremos relativos.
Si ya hemos estudiado el crecimiento y decrecimiento de una función habrá:
1 Un máximo en el punto, de la función, en la que esta pasa de creciente a decreciente.
2 Un mínimo en el punto, de la función, en la que esta pasa de decreciente a creciente.
Concavidad y convexidad
Para calcular los intervalos la concavidad y convexidad de una función seguiremos los siguientes pasos:
1 Hallamos la derivada segunda y calculamos sus raíces.
2 Formamos intervalos abiertos con los ceros (raíces) de la derivada segunda y los puntos de discontinuidad (si los hubiese).
3 Tomamos un valor de cada intervalo, y hallamos el signo que tiene en la derivada segunda.
4 Escribimos los intervalos.
Puntos de inflexión
Para hallar los puntos de inflexión, seguiremos los siguientes pasos:
1 Hallamos la derivada segunda y calculamos sus raíces.
2 Realizamos la derivada tercera, y calculamos el signo que toman en ella los ceros de derivada segunda y si:
Tenemos un punto de inflexión.
3 Calculamos la imagen (en la función) del punto de inflexión.
Si ya hemos estudiado la concavidad y convexidad de una función habrá:
Un punto de inflexión en el punto, de la función, en los puntos en que esta pasa de cóncava a convexa o vicecersa.
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
El Punto de inflexión en el ejercicio 2: f(x) = x^3 + x + 1 debe ser (0, 1)
Hola agradecemos tu comentario, tenias razón era un error que ya se corrigió.