
Cómo encontrar una la función inversa
Recordemos que la función inversa de  se define como aquella función
se define como aquella función  tal que
tal que 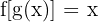 y
y 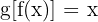 . Por lo tanto, la podemos obtener a partir de
. Por lo tanto, la podemos obtener a partir de  .
.
Asimismo, la función inversa de  se suele denotar como
se suele denotar como  (notemos que el
(notemos que el  en la expresión anterior no se refiere a un exponente negativo, sino que solo indica que es la función inversa).
en la expresión anterior no se refiere a un exponente negativo, sino que solo indica que es la función inversa).
Nota: en general, para que una función  tenga una función inversa, es necesario que la función sea uno-a-uno (o biyectiva). Cuando no se cumple esto, es necesario restringir el dominio.
tenga una función inversa, es necesario que la función sea uno-a-uno (o biyectiva). Cuando no se cumple esto, es necesario restringir el dominio.
Recordemos que una función uno-a-uno es aquella función que a cada elemento del dominio le asigna un valor diferente en el rango. Es decir, si 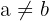 entonces
entonces 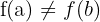 .
.
Método para encontrar la función inversa
1 Sustituye a  por
por  .
.
2 Despera la variable  . Por lo que obtenemos una expresión de la forma
. Por lo que obtenemos una expresión de la forma 
3 En 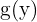 sustituye las
sustituye las  por
por  .
.
4 Por último, cambia el  del lado izquierdo por
del lado izquierdo por  .
.
Ejemplo: Consideremos la función 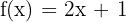 . Seguiremos el procedimiento para encontrar a la función inversa:
. Seguiremos el procedimiento para encontrar a la función inversa:
1 Sustituimos  por
por  :
: 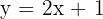 .
.
2 Despejamos  :
:
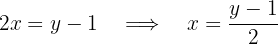
donde 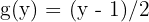
3 Intercambiamos las  por
por  :
:
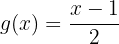
4 Luego cambiamos la  del lado izquierdo por
del lado izquierdo por  :
:
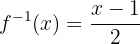
Por último, comprobamos que la función sí sea la inversa:
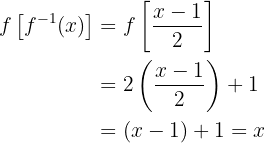
de donde podemos observar que se cumple que  .
.
Ejercicios propuestos
1 Encuentra la función inversa de la siguiente función lineal:
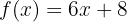
Encontraremos la función sin enlistar los pasos. Tenemos  , donde sustituimos
, donde sustituimos  por
por  :
:
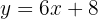
Luego, despejamos  :
:
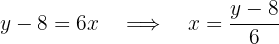
Por último, sustituimos  for
for  y
y  por
por  :
:
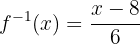
la cual es la función inversa.
2 Encuentra la función inversa de la siguiente función

Primero sustituimos  por
por  :
:
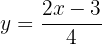
Luego despejamos  :
:

Es decir,

Por último, sustituimos  por
por  y
y  por
por  :
:
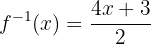
la cual es la función inversa.
3 Encuenta la función inversa de la siguiente función (no es necesario que simpliques):
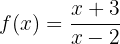
Empezamos sustituyendo  por
por  :
:
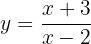
Luego despejamos  . Para esto primero multiplicamos por
. Para esto primero multiplicamos por  :
:

Luego pasamos las  a un lado de la ecuación y los términos restantes al otro:
a un lado de la ecuación y los términos restantes al otro:
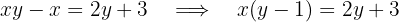
Por último, dividimos por 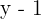 :
:
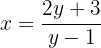
Por lo tanto, la función inversa es
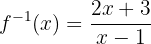
4 Calcula la función inversa de la siguiente función cuadrática
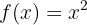
Notemos que  no es una función uno-a-uno (por ejemplo
no es una función uno-a-uno (por ejemplo 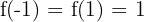 ). Por lo tanto, no tiene una función inversa en todo el dominio.
). Por lo tanto, no tiene una función inversa en todo el dominio.
Sin embargo, si consideramos como dominio al intervalo  , entonces la función será uno-a-uno. En este caso, la inversa se obtiene de la siguiente manera:
, entonces la función será uno-a-uno. En este caso, la inversa se obtiene de la siguiente manera:

Despejando  (y utilizando el hecho de que
(y utilizando el hecho de que 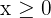 en el dominio restringido):
en el dominio restringido):
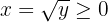
Por lo tanto, en este caso la función inversa es
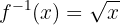
Por otro lado, si restringiéramos el dominio a 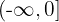 , entonces la función inversa se obtiene de la siguiente manera:
, entonces la función inversa se obtiene de la siguiente manera:

Luego despejamos  (que satisface
(que satisface 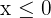 ):
):
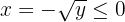
Por consiguiente, la función inversa es

Esto significa que 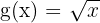 es la inversa de
es la inversa de  solo cuando el dominio son los números reales no-negativos
solo cuando el dominio son los números reales no-negativos  . Si el dominio son todos los números reales, la función no tiene inversa.
. Si el dominio son todos los números reales, la función no tiene inversa.
5 Encuenca la función inversa de la siguiente función
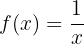
Empezamos sustituyendo  por
por  :
:
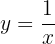
Luego despejamos  :
:
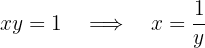
Por lo que la función inversa es
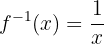
6 Encuenta la función inversa de la siguiente función:
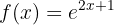
Empezamos sustituyendo  por
por  :
:
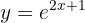
Luego, recordemos que el logaritmo natural satisface que
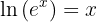
Así, aplicamos el logaritmo natural a ambos lados de la ecuación:
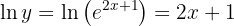
de este modo,
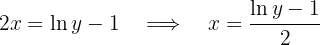
Por tanto, la función inversa es
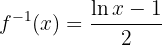
7 Encuentra la función inversa de la siguiente función
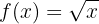
Las funciones radicales sí son uno-a-uno, por lo tanto, sí tiene función inversa:

donde sabemos que  . Luego elevamos al cuadrado ambos lados de la ecuación:
. Luego elevamos al cuadrado ambos lados de la ecuación:
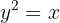
Por tanto, la función inversa es

donde 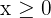 (como hacemos el cambio de
(como hacemos el cambio de  por
por  , entonces al final
, entonces al final  es quien satisface que
es quien satisface que 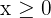 ).
).
En otras palabras, para que 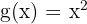 sea la función inversa de
sea la función inversa de  , se debe cumplir que
, se debe cumplir que  tenga como dominio sólo a
tenga como dominio sólo a  .
.
8 Encuentra la función inversa de

Sabemos que la función de raíz cubica es uno-a-uno, tiene como rango a todos los números reales, y su rango también son todos los números reales. Por lo tanto, tendrá una inversa cuyo dominio son todos los reales:

Elevamos al cubo ambos lados:

es decir,
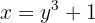
Por lo tanto, la función inversa es
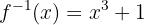
9 Encuentra la función inversa de

Asimismo, verifica que
a 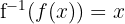
b 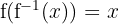
Primero encontramos la función inversa, para eso sustituimos  por
por  :
:

Luego, despejamos  :
:

es decir,
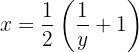
Ya tenemos  despejada. Sin embargo, simplificamos un poco:
despejada. Sin embargo, simplificamos un poco:
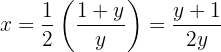
Por tanto, la inversa es

Ahora, verificamos lo que se nos pidió:
a Primero verificamos que 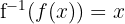 . Para ello, sustituimos
. Para ello, sustituimos  por su valor
por su valor
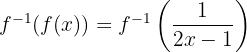
Luego, evaluamos  con el argumento dado,
con el argumento dado,
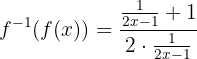
Simplificamos,

es decir,
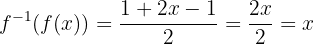
Por lo que se satisface la primera relación.
b Ahora verificaremos que 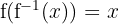 . Primero sustituimos
. Primero sustituimos  por su expresión:
por su expresión:
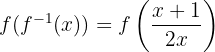
Luego evaluamos  :
:
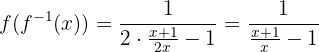
es decir,
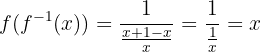
por tanto, la segunda relación también se cumple.
10 Calcula la inversa de la siguiente función
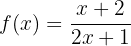
y verifica que 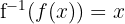 .
.
Empezamos calculando la inversa, por lo que sustituimos  por
por  :
:
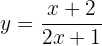
Luego, despejamos  ; por lo que multiplicamos por
; por lo que multiplicamos por  :
:

Después, pasamos los términos con  hacia el lado izquierdo de la igualdad, y los términos restantes al lado derecho:
hacia el lado izquierdo de la igualdad, y los términos restantes al lado derecho:
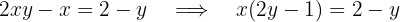
Por lo tanto,
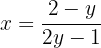
Es decir, la función inversa es
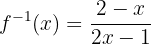
Ahora verificaremos que se cumpla que 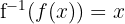 . Primero sustituimos la expresión de
. Primero sustituimos la expresión de  :
:

Ahora evaluamos la inversa:
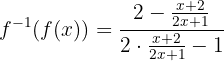
Simplificamos:
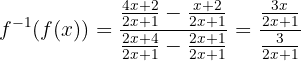
Luego:

Por tanto, la relación sí se cumple.
11 Calcula la inversa de la función 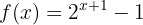
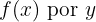 , luego depejamos para
, luego depejamos para  :
: 
Es decir,
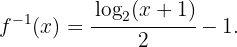
12 Calcula la inversa de la función 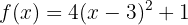 en el dominio apropiado.
en el dominio apropiado.
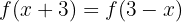 . Entonces, buscamos la inversa en el rango
. Entonces, buscamos la inversa en el rango  . Comenzamos por sustituir
. Comenzamos por sustituir 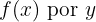 , luego depejamos para
, luego depejamos para  :
: 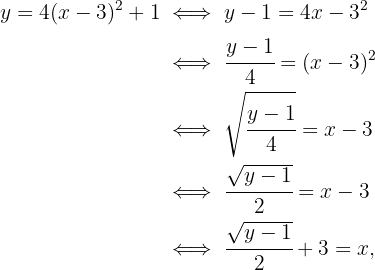
Es decir,
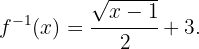
13 Calcula la inversa de la función 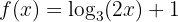
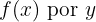 , luego depejamos para
, luego depejamos para  :
: 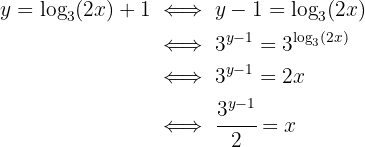
Es decir,

14 Calcula la inversa de la función 
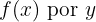 , luego depejamos para
, luego depejamos para  :
: 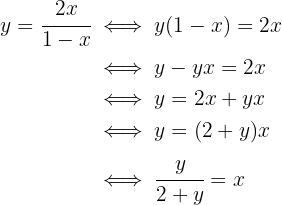
Es decir,
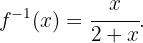
15 Calcula la inversa de la función 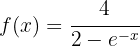
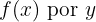 , luego depejamos para
, luego depejamos para  :
: 
Es decir,
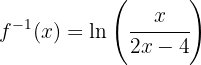
Encuentra la función inversa de la siguiente función lineal:
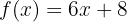
Encontraremos la función sin enlistar los pasos. Tenemos  , donde sustituimos
, donde sustituimos  por
por  :
:
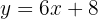
Luego, despejamos  :
:
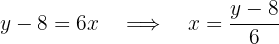
Por último, sustituimos  for
for  y
y  por
por  :
:
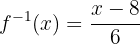
la cual es la función inversa.
Encuentra la función inversa de la siguiente función

Primero sustituimos  por
por  :
:
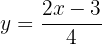
Luego despejamos  :
:

Es decir,

Por último, sustituimos  por
por  y
y  por
por  :
:
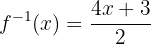
la cual es la función inversa.
Encuenta la función inversa de la siguiente función (no es necesario que simpliques):
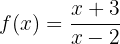
Empezamos sustituyendo  por
por  :
:
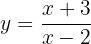
Luego despejamos  . Para esto primero multiplicamos por
. Para esto primero multiplicamos por  :
:

Luego pasamos las  a un lado de la ecuación y los términos restantes al otro:
a un lado de la ecuación y los términos restantes al otro:
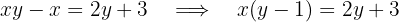
Por último, dividimos por 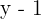 :
:
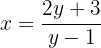
Por lo tanto, la función inversa es
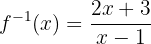
Calcula la función inversa de la siguiente función cuadrática
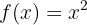
Notemos que  no es una función uno-a-uno (por ejemplo
no es una función uno-a-uno (por ejemplo 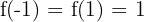 ). Por lo tanto, no tiene una función inversa en todo el dominio.
). Por lo tanto, no tiene una función inversa en todo el dominio.
Sin embargo, si consideramos como dominio al intervalo  , entonces la función será uno-a-uno. En este caso, la inversa se obtiene de la siguiente manera:
, entonces la función será uno-a-uno. En este caso, la inversa se obtiene de la siguiente manera:

Despejando  (y utilizando el hecho de que
(y utilizando el hecho de que 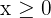 en el dominio restringido):
en el dominio restringido):
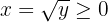
Por lo tanto, en este caso la función inversa es
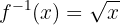
Por otro lado, si restringiéramos el dominio a 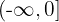 , entonces la función inversa se obtiene de la siguiente manera:
, entonces la función inversa se obtiene de la siguiente manera:

Luego despejamos  (que satisface
(que satisface 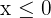 ):
):
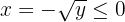
Por consiguiente, la función inversa es

Esto significa que 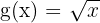 es la inversa de
es la inversa de  solo cuando el dominio son los números reales no-negativos
solo cuando el dominio son los números reales no-negativos  . Si el dominio son todos los números reales, la función no tiene inversa.
. Si el dominio son todos los números reales, la función no tiene inversa.
Encuenca la función inversa de la siguiente función
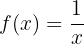
Empezamos sustituyendo  por
por  :
:
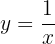
Luego despejamos  :
:
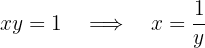
Por lo que la función inversa es
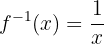
Encuenta la función inversa de la siguiente función:
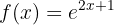
Empezamos sustituyendo  por
por  :
:
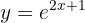
Luego, recordemos que el logaritmo natural satisface que
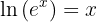
Así, aplicamos el logaritmo natural a ambos lados de la ecuación:
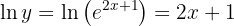
de este modo,
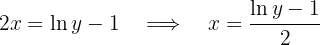
Por tanto, la función inversa es
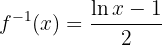
Encuentra la función inversa de la siguiente función
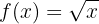
Las funciones radicales sí son uno-a-uno, por lo tanto, sí tiene función inversa:

donde sabemos que  . Luego elevamos al cuadrado ambos lados de la ecuación:
. Luego elevamos al cuadrado ambos lados de la ecuación:
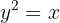
Por tanto, la función inversa es

donde 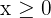 (como hacemos el cambio de
(como hacemos el cambio de  por
por  , entonces al final
, entonces al final  es quien satisface que
es quien satisface que 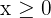 ).
).
En otras palabras, para que 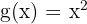 sea la función inversa de
sea la función inversa de  , se debe cumplir que
, se debe cumplir que  tenga como dominio sólo a
tenga como dominio sólo a  .
.
Encuentra la función inversa de

Sabemos que la función de raíz cubica es uno-a-uno, tiene como rango a todos los números reales, y su rango también son todos los números reales. Por lo tanto, tendrá una inversa cuyo dominio son todos los reales:

Elevamos al cubo ambos lados:

es decir,
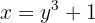
Por lo tanto, la función inversa es
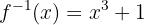
Encuentra la función inversa de

Asimismo, verifica que
a 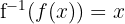
b 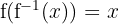
Primero encontramos la función inversa, para eso sustituimos  por
por  :
:

Luego, despejamos  :
:

es decir,
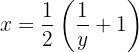
Ya tenemos  despejada. Sin embargo, simplificamos un poco:
despejada. Sin embargo, simplificamos un poco:
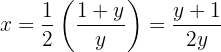
Por tanto, la inversa es

Ahora, verificamos lo que se nos pidió:
a Primero verificamos que 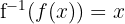 . Para ello, sustituimos
. Para ello, sustituimos  por su valor
por su valor
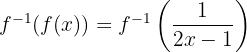
Luego, evaluamos  con el argumento dado,
con el argumento dado,
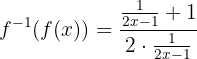
Simplificamos,

es decir,
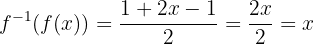
Por lo que se satisface la primera relación.
b Ahora verificaremos que 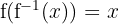 . Primero sustituimos
. Primero sustituimos  por su expresión:
por su expresión:
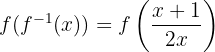
Luego evaluamos  :
:
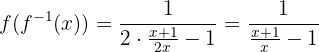
es decir,
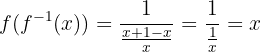
por tanto, la segunda relación también se cumple.
Calcula la inversa de la siguiente función
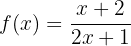
y verifica que 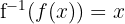 .
.
Empezamos calculando la inversa, por lo que sustituimos  por
por  :
:
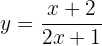
Luego, despejamos  ; por lo que multiplicamos por
; por lo que multiplicamos por  :
:

Después, pasamos los términos con  hacia el lado izquierdo de la igualdad, y los términos restantes al lado derecho:
hacia el lado izquierdo de la igualdad, y los términos restantes al lado derecho:
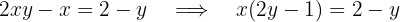
Por lo tanto,
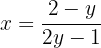
Es decir, la función inversa es
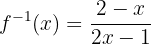
Ahora verificaremos que se cumpla que 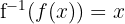 . Primero sustituimos la expresión de
. Primero sustituimos la expresión de  :
:

Ahora evaluamos la inversa:
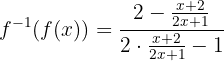
Simplificamos:
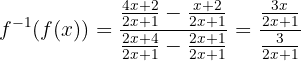
Luego:

Por tanto, la relación sí se cumple.
Calcula la inversa de la función 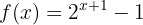
Comenzamos por sustituir 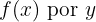 , luego depejamos para
, luego depejamos para  :
:
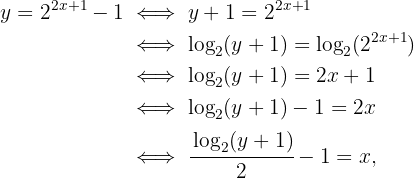
Es decir,
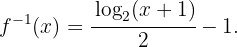
Calcula la inversa de la función 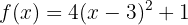 en el dominio apropiado.
en el dominio apropiado.
Primero notemos que esta no es una función inyectiva. De hecho, 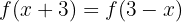 . Entonces, buscamos la inversa en el rango
. Entonces, buscamos la inversa en el rango  . Comenzamos por sustituir
. Comenzamos por sustituir 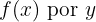 , luego depejamos para
, luego depejamos para  :
:
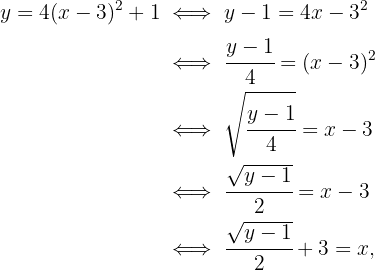
Es decir,
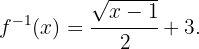
Calcula la inversa de la función 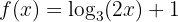
Comenzamos por sustituir 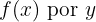 , luego depejamos para
, luego depejamos para  :
:
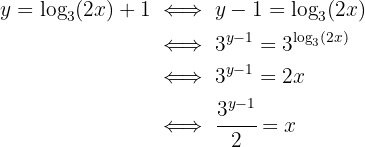
Es decir,
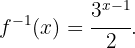
Calcula la inversa de la función 
Comenzamos por sustituir 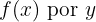 , luego depejamos para
, luego depejamos para  :
:
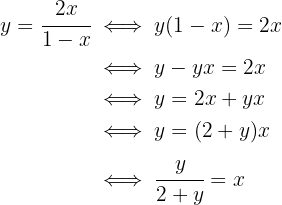
Es decir,
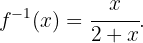
Calcula la inversa de la función 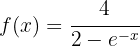
Comenzamos por sustituir 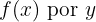 , luego depejamos para
, luego depejamos para  :
:
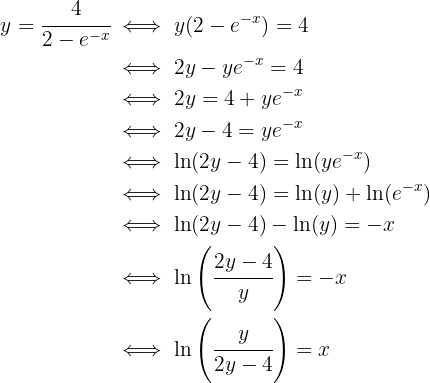
Es decir,
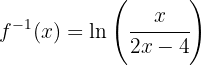
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.
Podrían mostrar los pares ordenados para graficarlo, gracias