Arrastra cada gráfica a la tabla que corresponda
1
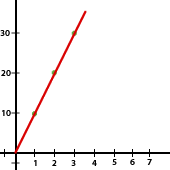
| Nº de días | 1 | 2 | 3 | 6 | 8 | 10 |
| Precio (en €) | 10 | 20 | 30 | 60 | 80 | 100 |
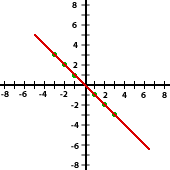
| Número | -3 | -2 | -1 | 1 | 2 | 3 |
|---|---|---|---|---|---|---|
| Opuesto | 3 | 2 | 1 | −1 | −2 | −3 |
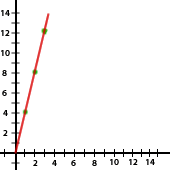
| Lado (en cm) | 1 | 2 | 3 | 5 | 10 | 20 |
| Perímetro (en cm) | 4 | 8 | 12 | 20 | 40 | 80 |
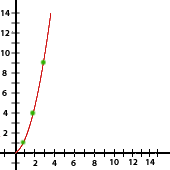
| Lado (en cm) | 1 | 2 | 3 | 6 | 8 | 9 | 11 |
| Área (en cm²) | 1 | 4 | 9 | 36 | 64 | 81 | 121 |
|
| ||||||||||||||||||||||||||||||
 |  | ||||||||||||||||||||||||||||||
|
| ||||||||||||||||||||||||||||||
 |  |
Escoge el enunciado adecuado para cada una de estas dos gráficas:
2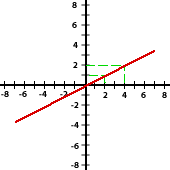
3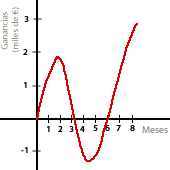
Escoge la gráfica adecuada para cada enunciado:
4Ana salió a pasear a las 4 de la tarde. A los 15 minutos se encontró con Pablo y estuvieron hablando parados media hora. El chico decidió acompañarla y caminaron durante tres cuartos de hora hasta llegar a casa de Marta. Allí pararon 35 minutos para merendar y descansar. Después volvieron a casa de la chica sin hacer ninguna parada, para lo que emplearon 55 minutos.
En primer lugar, sumando el tiempo que Ana está en la calle podemos deducir que llega a casa a las 7 de la tarde, lo que nos hace descartar la segunda opción. En efecto,
15 + 30 + 45 + 35 + 55 = 180 min = 3 h Ana pasa 3 horas fuera de casa.
Como salió de casa a las 4 de la tarde, entonces llega a casa a las 7 de la tarde, es decir, a las 19:00 horas.
Ana hace dos paradas, una al encontrarse con Pablo y otra para merendar en casa de Marta, por tanto, esto debe aparecer como dos tramos de función constante en la gráfica, ya que en esos inervalos de tiempo no se recorre espacio alguno, no aumentando así ni disminuyendo la distancia a casa de Ana. Por tanto, también podemos descartar la primera gráfica, puesto que en ella sólo hay un tramo de función constante.
Por tanto, la gráfica correcta es la última:
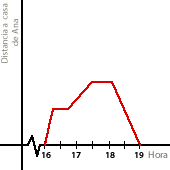
5Queremos llenar un recipiente como el de la figura dejando abierto un grifo que deja caer el agua a velocidad constante. Y queremos encontrar la tabla que relaciona el tiempo transcurrido con la velocidad de llenado del recipiente.
Debemos observar que al principio la velocidad de llanado será mayor, puesto que la zona inferior del recipiente (que va a ser la que se llena primero) es más estrecha que la superior. Por tanto, la gráfica correcta debe indicar una mayor velocidad al principio y menor más adelante, es decir, algo como lo que se muestra en la siguiente gráfica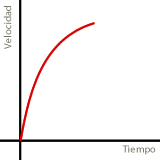
Si tienes dudas puedes consultar la teoría
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
El Punto de inflexión en el ejercicio 2: f(x) = x^3 + x + 1 debe ser (0, 1)
Hola agradecemos tu comentario, tenias razón era un error que ya se corrigió.