Ejercicios de optimización utilizando derivadas.
Ejercicios propuestos
El valor de un rubí es proporcional al cuadrado de su peso. Divide un rubí de 
g en dos partes de 
gramos y de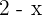 
gramos, de forma que la suma de los valores de los dos rubíes formados sea mínima.
El valor de dos rubíes será, en función del peso de uno de ellos:
Calculamos la derivada e igualamos a cero para encontrar valores críticos:
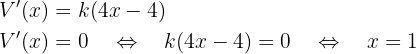
Calculamos la derivada segunda y sustituimos:
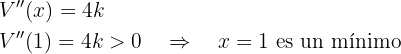
Por tanto, el rubí se ha de dividir en dos partes iguales de 
g.
Encontrar, de entre todas las rectas que pasan por por el punto 
aquella que forma con la partes positivas de los ejes de coordenadas un triángulo de área mínima.
De la forma punto-pendiente de la recta tenemos que la ecuación de la recta que pasa por el punto es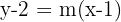
Puesto que queremos que los vértices queden en las partes positivas de los ejes coordenados necesitamos el valor que toma cuando 
y el valor que toma 
cuando 
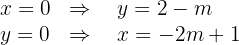
Por tanto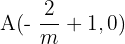 
y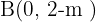 
vértices del triangulo.
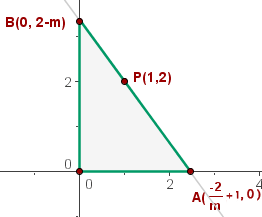
Ahora bien, queremos que el área del triangulo formado por la recta sea mínima, recordemos que el area del triangulo es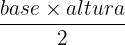 
en este caso queda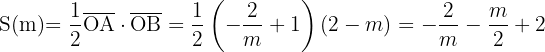 
Calculamos la derivada e igualamos a cero para encontrar valores críticos: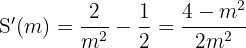 
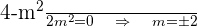
Notemos que con 
no se formaría un triángulo porque las coordenadas de A y B coinciden con el origen de coordenadas, por tanto tomamos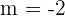 
Calculamos la derivada segunda y sustituimos:
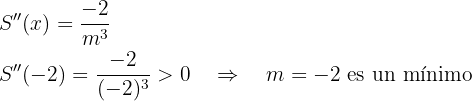
Por tanto, la recta es la que tiene pendiente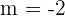
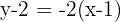
Una boya, formada por dos conos rectos de hierro unidos por sus bases ha de ser construido mediante dos placas circulares de 
m de radio. Calcular las dimensiones de la boya para que su volumen sea máximo.
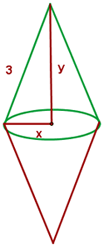
Recordemos que la formula del volumen del cono es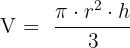
en este caso de acuerdo a la figura tendríamos que la función a optimizar es 
Relacionamos las variables: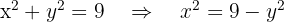 
Sustituimos en la función: 
Derivamos, igualamos a cero y calculamos las raíces.
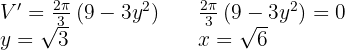
Realizamos la derivada segunda para comprobar el resultado obtenido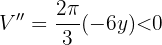 
Hallar dos números que sumados den 20 y cuyo producto sea máximo.
Sean , los números buscados. El problema a resolver seria el siguiente:
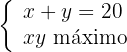
Sea 
y como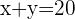 
entonces 
, sustituyendo resulta: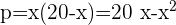
Vamos a calcular el (o los) máximo(s) de la función 
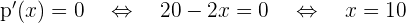
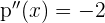
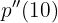
Cuáles son las dimensiones de un campo rectangular de 
de superficie, para poderlo cercar con una valla de longitud mínima.
Sean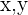 
los lados del rectángulo, sabemos por la formula del área del rectángulo que
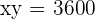
Por otro lado, la superficie que tenemos que vallar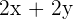 
, es decir, es la función a minimizar.Tenemos que 
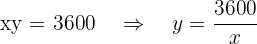Llamando 
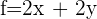y sustituyendo 
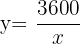obtenemos:
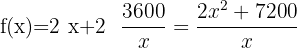
Vamos a minimizar 
: 
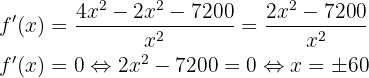
Calculando la segunda derivada y sustituyendo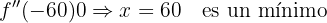 
Por tanto, las dimensiones son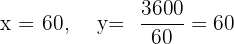 
Descomponer el número 
en dos sumandos tales que el quíntuplo del cuadrado del primero más el séxtuplo del cuadrado del segundo sea un mínimo.
Queremos descomponer el numero en dos sumandos, entonces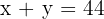 
y queremos que el quíntuplo del cuadrado del primero más el séxtuplo del cuadrado del segundo sea un mínimo por tanto 
Puesto que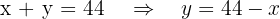 
sustituimos "" 
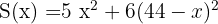
Derivando e igualando a cero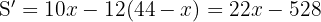 
Calculando la segunda derivada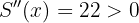 
Por tanto mínimo y los números son
El beneficio neto mensual, en millones de euros, de una empresa que fabrica autobuses viene dado por la función:
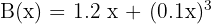donde es el número de autobuses fabricados en un mes. Calcula la producción mensual que hacen máximo el beneficio.
Derivamos la función del beneficio mensual e igualamos a cero 
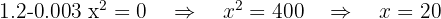
Calculamos la segunda derivada y sustituimos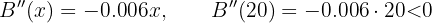 
Por tanto máximo.
Halla dos números tales que el cuadrado de uno multiplicado por el otro sea máximo, si la suma de dichos números es 
.
Conisderemos 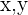los numero buscados, tenemos que 
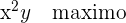
Llamamos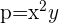 
.
Puesto que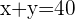 
entonces se tiene que 
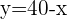y por tanto:
Vamos a maximizar la función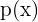 
Resumir con IA:
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.
Podrían mostrar los pares ordenados para graficarlo, gracias