Área máxima de un rectángulo inscrito en un círculo
Hallar los lados del rectángulo de área máxima inscrito en un círculo de radio  .
.
1 Consideramos  la base y la altura del rectángulo.
la base y la altura del rectángulo.
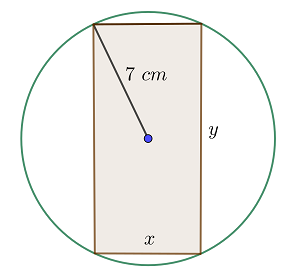
2 Función a optimizar
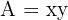
3Relacionamos las variables, para ello consideramos la diagonal de rectángulo y aplicamos el teorema de Pitágoras
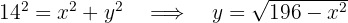
4 Sustituimos en la función a optimizar
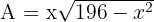
5 Derivamos la función a optimizar
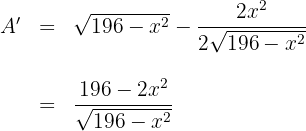
6 Igualamos la derivada a cero y calculamos las raíces
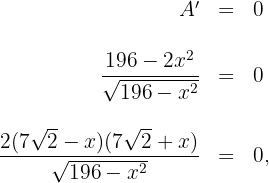
entonces 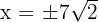 , pero solamente consideramos el resultado positivo
, pero solamente consideramos el resultado positivo
Encontramos la altura
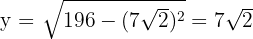
7 Realizamos la derivada segunda para comprobar el resultado obtenido
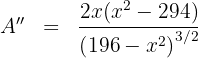
Sustituimos 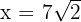
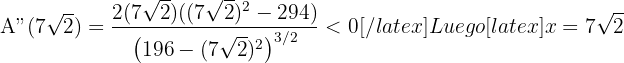 maximiza el área. Así, el rectángulo de área máxima es aquel cuya base y altura es
maximiza el área. Así, el rectángulo de área máxima es aquel cuya base y altura es 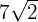
Área máxima de un rectángulo inscrito en una elipse
Hallar los lados del rectángulo de área máxima inscrito en la elipse 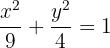
1 Consideramos 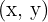 un vértice del rectángulo en la elipse, así por la simetría de la elipse respecto al origen, la base del rectángulo es
un vértice del rectángulo en la elipse, así por la simetría de la elipse respecto al origen, la base del rectángulo es  y su altura es
y su altura es 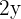
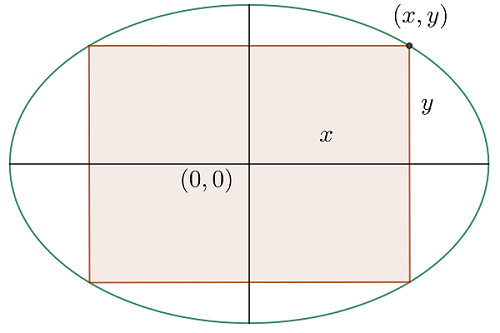
2 Función a optimizar
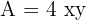
3Relacionamos las variables, para ello consideramos despejamos una de las variables en la ecuación de la elipse

4 Sustituimos en la función a optimizar
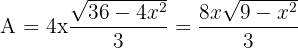
5 Derivamos la función a optimizar
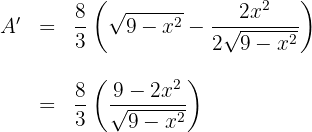
6 Igualamos la derivada a cero y calculamos las raíces
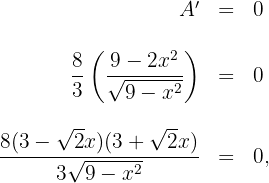
entonces 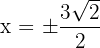 , pero solamente consideramos el resultado positivo. Así, la base es
, pero solamente consideramos el resultado positivo. Así, la base es 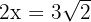
Encontramos la altura
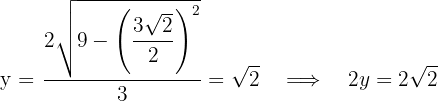
7 Realizamos la derivada segunda para comprobar el resultado obtenido
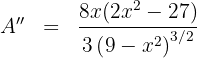
Sustituimos 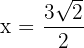
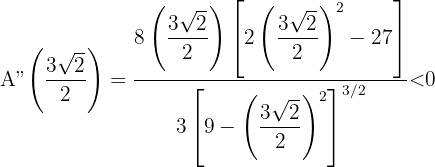
Luego 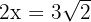 maximiza el área. Así, el rectángulo de área máxima es aquel cuya base y altura son
maximiza el área. Así, el rectángulo de área máxima es aquel cuya base y altura son 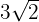 y
y 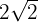
Área lateral mínima de un cono
Se pretende fabricar una cono (sin tapa) de volumen 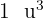 . ¿Cuáles deben ser sus dimensiones para que se utilice el mínimo posible de material?
. ¿Cuáles deben ser sus dimensiones para que se utilice el mínimo posible de material?
1 Consideramos  el radio de la base del cono y
el radio de la base del cono y  su altura
su altura
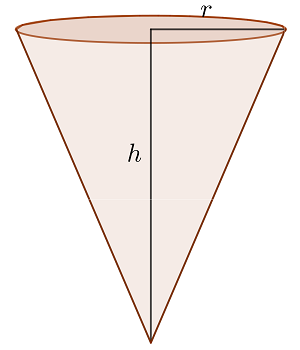
2 Función a optimizar
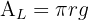
3Relacionamos las variables, para ello consideramos el volumen y la generatriz
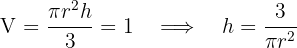
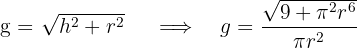
4 Sustituimos en la función a optimizar
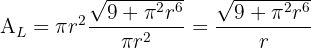
5 Derivamos la función a optimizar
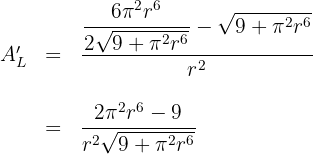
6 Igualamos la derivada a cero y calculamos las raíces
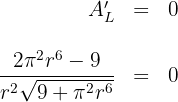
entonces 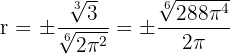 , pero solamente consideramos el resultado positivo
, pero solamente consideramos el resultado positivo
Encontramos la altura
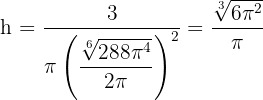
7 Realizamos la derivada segunda para comprobar el resultado obtenido
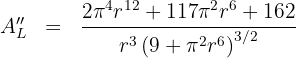
Sustituimos 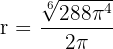
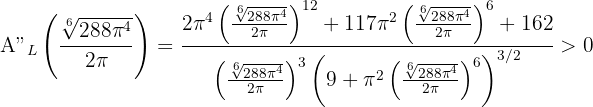
Luego 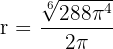 minimiza el área lateral. Así, las medidas del cono que minimizan el área lateral es aquel cuyo radio y altura son
minimiza el área lateral. Así, las medidas del cono que minimizan el área lateral es aquel cuyo radio y altura son 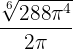 y
y 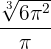
Producto máximo de dos números
Encontrar dos números positivos cuya suma sea  y tal que el producto de uno de ellos con el cuadrado del otro sea máximo.
y tal que el producto de uno de ellos con el cuadrado del otro sea máximo.
1 Consideramos 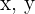 los dos número positivos cuya suma es
los dos número positivos cuya suma es  .
.
2Función a optimizar:
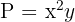
3Relacionamos las variables, para ello consideramos la suma de ambos números

4Sustituimos en la función a optimizar
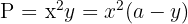
5Derivamos la función a optimizar
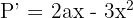
6 Igualamos la derivada a cero y calculamos las raíces
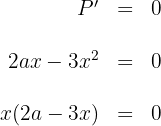
entonces 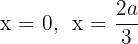 , pero solamente consideramos el resultado positivo
, pero solamente consideramos el resultado positivo
Encontramos el valor del otro número
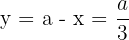
7 Realizamos la derivada segunda para comprobar el resultado obtenido
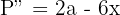
Sustituimos 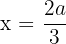
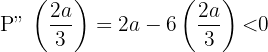
Luego 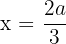 maximiza el producto. Así, los números que maximizan el producto so n
maximiza el producto. Así, los números que maximizan el producto so n 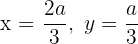
Área mínima de dos figuras
Se tiene un alambre de 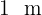 de longitud y se desea dividirlo en dos trozos para formar con uno de ellos un círculo y con el otro un triángulo equilátero. Determinar la longitud que se ha de dar a cada uno de los trozos para que la suma de las áreas del círculo y del triángulo sea mínima.
de longitud y se desea dividirlo en dos trozos para formar con uno de ellos un círculo y con el otro un triángulo equilátero. Determinar la longitud que se ha de dar a cada uno de los trozos para que la suma de las áreas del círculo y del triángulo sea mínima.
1 Consideramos  el radio del círculo y
el radio del círculo y 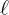 el lado del triángulo equilátero.
el lado del triángulo equilátero.
2Función a optimizar:
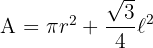
3Relacionamos las variables, para ello consideramos la suma de ambos perímetros
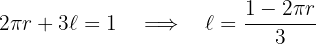
4Sustituimos en la función a optimizar
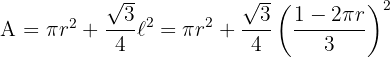
5Derivamos la función a optimizar
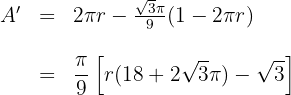
6 Igualamos la derivada a cero y calculamos las raíces
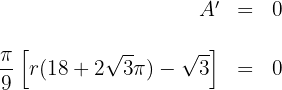
entonces 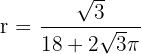
Encontramos el valor del lad del triángulo
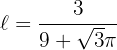
7 Realizamos la derivada segunda para comprobar el resultado obtenido
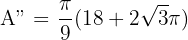
Sustituimos 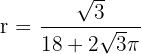
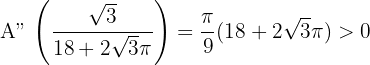
Luego 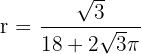 minimiza el área. Así, el alambre se divide en trozos de
minimiza el área. Así, el alambre se divide en trozos de 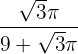 para el círculo y
para el círculo y 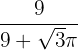 para el triángulo equilátero
para el triángulo equilátero
Área máxima de un rectángulo inscrito en un triángulo acutángulo
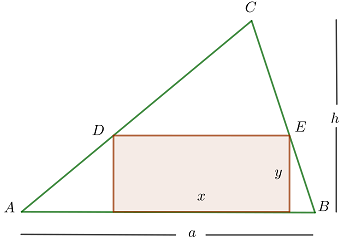
Hallar las dimensiones del mayor rectángulo inscrito en un triángulo acutángulo si uno de los lados del rectángulo está contenido en la base del triángulo.
1 Consideramos el triángulo acutángulo  de base
de base  y altura
y altura  , y el rectángulo de lados
, y el rectángulo de lados 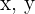 con el lado
con el lado  contenido en la base del triángulo y lado opuesto con extremos
contenido en la base del triángulo y lado opuesto con extremos 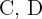 en los otros dos lado del triángulo
en los otros dos lado del triángulo
2 Función a optimizar
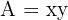
3Relacionamos las variables, para ello consideramos los triángulos semejantes  y
y 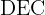

4 Sustituimos en la función a optimizar
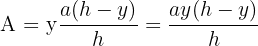
5 Derivamos la función a optimizar
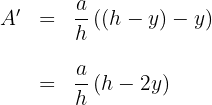
6 Igualamos la derivada a cero y calculamos las raíces
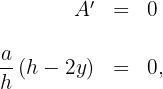
entonces 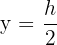
Encontramos la base
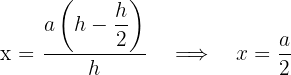
7 Realizamos la derivada segunda para comprobar el resultado obtenido
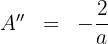
Sustituimos 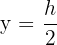
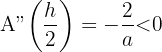
Luego 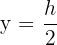 maximiza el área del rectángulo. Así, el rectángulo de área máxima buscado, es aquel cuya base y altura son
maximiza el área del rectángulo. Así, el rectángulo de área máxima buscado, es aquel cuya base y altura son  y
y  , respectivamente.
, respectivamente.
Costo mínimo de un contenedor cilíndrico
Hallar las dimensiones que hacen mínimo el coste de un contenedor que tiene forma de cilíndro, sabiendo que su volumen ha de ser 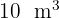 y el coste de su construcción por
y el coste de su construcción por 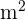 es de
es de  € para la base;
€ para la base; 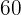 para la etapa y
para la etapa y  para cada pared lateral.
para cada pared lateral.
1 Consideramos 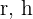 el radio y altura del cilíndro
el radio y altura del cilíndro
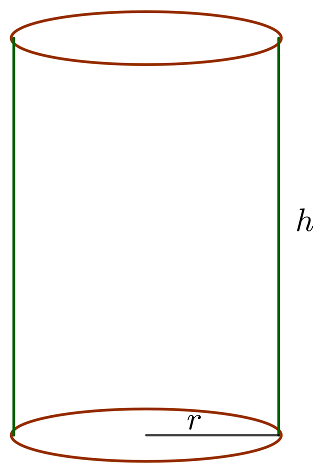
2 Función a optimizar
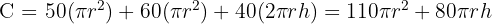
3Relacionamos las variables, para ello consideramos el volumen 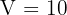 del recipiente
del recipiente
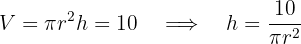
4 Sustituimos en la función a optimizar
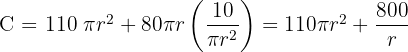
5 Derivamos la función a optimizar
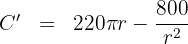
6 Igualamos la derivada a cero y calculamos las raíces
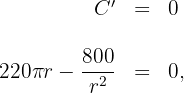
entonces 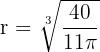
Encontramos la altura
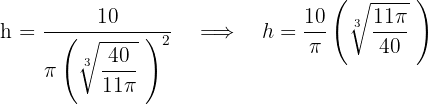
7 Realizamos la derivada segunda para comprobar el resultado obtenido
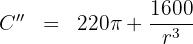
Sustituimos 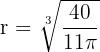
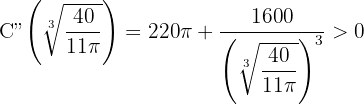
Luego 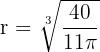 y
y 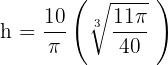 minimizan el costo del contenedor.
minimizan el costo del contenedor.
Perímetro mínimo
Un granjero quiere delimitar un terreno rectangular de 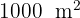 . El terreno debe estar cercado y dividido en dos partes iguales por medio de una cerca paralela a dos lados. ¿Cuáles son las dimensiones del terreno que emplea la mínima cantidad de cerca?
. El terreno debe estar cercado y dividido en dos partes iguales por medio de una cerca paralela a dos lados. ¿Cuáles son las dimensiones del terreno que emplea la mínima cantidad de cerca?
1 Consideramos el terreno con base  y altura
y altura 

2 Función a optimizar
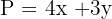
3Relacionamos las variables, para ello consideramos el área 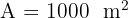 del terreno
del terreno
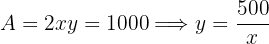
4 Sustituimos en la función a optimizar
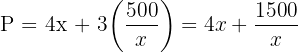
5 Derivamos la función a optimizar
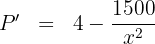
6 Igualamos la derivada a cero y calculamos las raíces
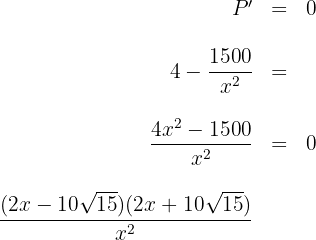
entonces 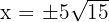 y elegimos el positivo.
y elegimos el positivo.
Encontramos la altura
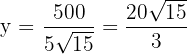
7 Realizamos la derivada segunda para comprobar el resultado obtenido
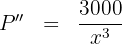
Sustituimos 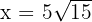
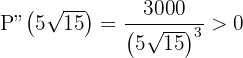
Luego 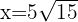 y
y 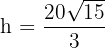 minimizan el costo de la cerca.
minimizan el costo de la cerca.
Tiempo mínimo
Una persona en una isla desea llegar a un punto  situado sobre una playa recta en tierra firme. Lapersona se encuentra a
situado sobre una playa recta en tierra firme. Lapersona se encuentra a 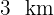 del punto
del punto  más próximo a la playa y el punto
más próximo a la playa y el punto  se encuentra a
se encuentra a 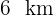 de
de  . Si la persona nada a
. Si la persona nada a 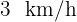 y camina a
y camina a 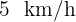 , determina en que punto sobre la playa debe llegar nadando para minimizar su tiempo.
, determina en que punto sobre la playa debe llegar nadando para minimizar su tiempo.
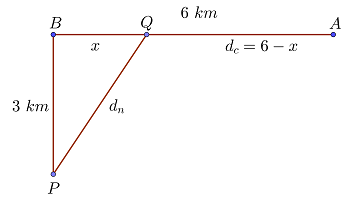
1 Consideramos  la distancia de
la distancia de  a el punto en la playa donde llega la persona nadando,
a el punto en la playa donde llega la persona nadando, 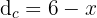 la distancia que recorre caminando
la distancia que recorre caminando
2 Función a optimizar
Primero calculamos la distancia nadada empleando el teorema de Pitágoras
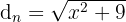
Los tiempos empleados son
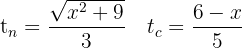
La función a optimizar es igual a la suma de los tiempos empleados
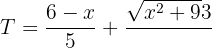
3 Derivamos la función a optimizar
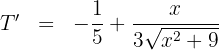
4 Igualamos la derivada a cero y calculamos las raíces
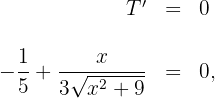
entonces 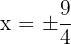 y tomamos el positivo.
y tomamos el positivo.
5 Realizamos la derivada segunda para comprobar el resultado obtenido
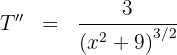
Sustituimos 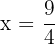
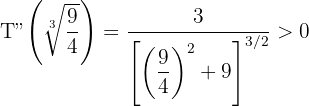
Luego el tiempo mínimo ocurre cuando 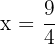 , entonces la persona debe llegar nadando a
, entonces la persona debe llegar nadando a 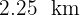 del punto
del punto  y caminar
y caminar 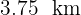 para llegar a su destino.
para llegar a su destino.
Área máxima de un triángulo isosceles
Un triángulo isosceles tiene perímetro  , ¿cuánto deben medir sus lados para que el área sea máxima?
, ¿cuánto deben medir sus lados para que el área sea máxima?
1 Consideramos  los lados iguales del triángulo isósceles,
los lados iguales del triángulo isósceles,  como base y
como base y  su altura
su altura
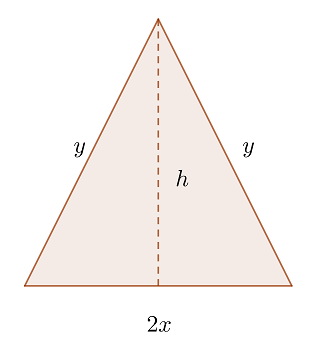
2 Función a optimizar
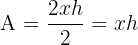
3Relacionamos las variables, para ello consideramos el perímetro y la altura
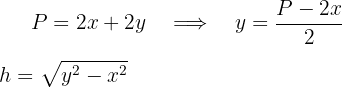
Sustituimos la expresión de  en la altura
en la altura
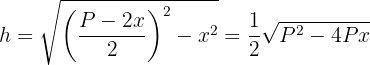
4 Sustituimos la expresión de la altura en la función a optimizar
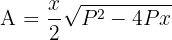
5 Derivamos la función a optimizar
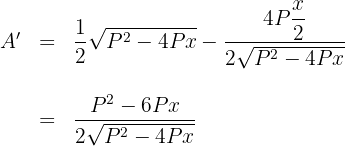
6 Igualamos la derivada a cero y calculamos las raíces
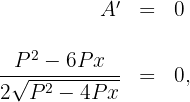
entonces 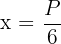 . Notemos que la derivada no está definida en
. Notemos que la derivada no está definida en 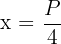
Encontramos el valor del lado 
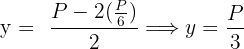
7 Realizamos la derivada segunda para comprobar el resultado obtenido
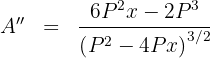
Sustituimos 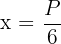
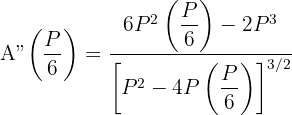 , luego el triángulo es equilátero.
, luego el triángulo es equilátero.
Resumir con IA:


Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Felicitaciones, muy interesantes los problemas y sobretodo las gráficas. ¿Pueden indicarme que programa utilizan?
Hola te agradecemos tu comentario, si te refieres a graficar te recomendamos geogebra, symbolat y otros mas.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.