Capítulos

¿Qué es infinito y cómo resolvemos ejercicios de limites?
Cuando resolvemos límites con frecuencia necesitamos operar con el infinito. Sin embargo, debemos recordar que el infinito no es un número. En algunas ocasiones lo vamos a operar como un número con el fin de encontrar límites, no obstante, debemos tener en cuenta que en muchas ocasiones el infinito no se comporta como un número.
Existen algunas ocasiones donde la operación con el infinito está indeterminada. Esta es una de esas ocasiones donde  no se comporta como un número. Cuando nos encontramos con algunas de esas operaciones indeterminadas, debemos hacer una ligera modificación a la función a la cual estamos calculando el límite con el fin de evitar la indeterminación. Esto se conoce como "evitar la indeterminación"
no se comporta como un número. Cuando nos encontramos con algunas de esas operaciones indeterminadas, debemos hacer una ligera modificación a la función a la cual estamos calculando el límite con el fin de evitar la indeterminación. Esto se conoce como "evitar la indeterminación"
La definición épsilon-delta del límite es la siguiente:
Un valor  es el límite de la función
es el límite de la función 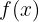 en
en  si para todo
si para todo 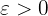 existe un
existe un 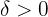 tal que para todo
tal que para todo  que satisface
que satisface 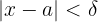 se cumple que
se cumple que 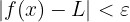 .
.
Verificar que se cumplen los criterios de la definición es una forma de demostrar que existe el límite para una función en un  dado.
dado.
Límites de una función elevada a otra función
Recordemos que la definición de  es:
es:
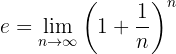
En algunos casos donde tenemos una indeterminación de la forma  será necesario reescribir la expresión de una forma similar a la definición de
será necesario reescribir la expresión de una forma similar a la definición de  ; de este modo podremos calcular el límite.
; de este modo podremos calcular el límite.
Límites con formas que no son indeterminadas.
Las formas  ,
,  ,
, 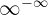 y
y 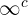 para algún
para algún 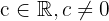 no son formas indeterminadas. Si obtenemos alguna de estas formas podemos calcular el límite con confianza.
no son formas indeterminadas. Si obtenemos alguna de estas formas podemos calcular el límite con confianza.
Ejercicios de límites
Utilizando la definición de límite (épsilon-delta), prueba que
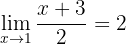
Consideremos un 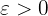 arbitrario. Debemos probar que existe un
arbitrario. Debemos probar que existe un 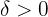 que satisfaga la definición de límite.
que satisfaga la definición de límite.
Deseamos que cuando 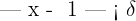 (que todavía no conocemos), se cumpla que:
(que todavía no conocemos), se cumpla que:
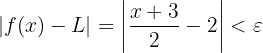
Si simplicamos un poco, tenemos:

Nota que estamos tratando de dejar 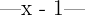 de un lado de la desigualdad para poder obtener una expresión para
de un lado de la desigualdad para poder obtener una expresión para 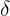 . Si multiplicamos por 2 ambos lados de la desigualdad, obtendremos:
. Si multiplicamos por 2 ambos lados de la desigualdad, obtendremos:
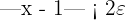
Por lo tanto, si tomamos 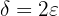 se cumple la desigualdad. Con lo que terminamos la demostración.
se cumple la desigualdad. Con lo que terminamos la demostración.
¿Qué significa esto?
Significa que para cualquier 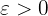 que nos den, siempre podremos encontrar un
que nos den, siempre podremos encontrar un 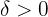 que satisfaga la definición debido a que ya tenemos la fórmula para ello —
que satisfaga la definición debido a que ya tenemos la fórmula para ello —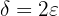 en este caso—.
en este caso—.
Por ejemplo, si tuviéramos 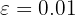 , entonces
, entonces  . Por lo tanto, si
. Por lo tanto, si 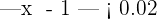 es equivalente a
es equivalente a
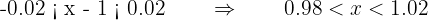 .
.
Es decir,  . Por lo tanto, si tomamos cualquier
. Por lo tanto, si tomamos cualquier  en el intervalo
en el intervalo 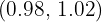 se va a cumplir que
se va a cumplir que

Por ejemplo, tomemos 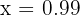 , entonces
, entonces 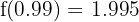 . De este modo:
. De este modo:
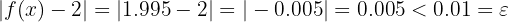
Similarmente, si tomamos 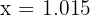 , entonces
, entonces 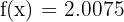 . Por lo que:
. Por lo que:
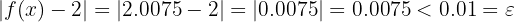
Observa la siguiente gráfica de  y determina los límites que se solicitan:
y determina los límites que se solicitan:
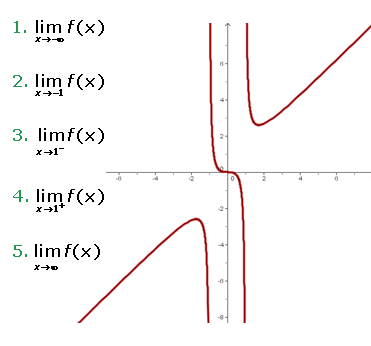
1 El primer límite que se nos pide es
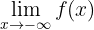
Notemos que cuando 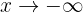 , es decir, cuando
, es decir, cuando  decrece "infinitamente", la función también decrece infinitamente. Por lo tanto,
decrece "infinitamente", la función también decrece infinitamente. Por lo tanto,
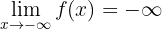
2Ahora se nos pide determinar
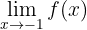
En este caso observemos que cuando  se acerca mucho a
se acerca mucho a  por la izquierda, la función decrece infinitamente. Por otro lado, cuando
por la izquierda, la función decrece infinitamente. Por otro lado, cuando  se acerca mucho a
se acerca mucho a  por la derecha, la función crece infinitamente. Por tanto, podemos concluir que el límite no existe.
por la derecha, la función crece infinitamente. Por tanto, podemos concluir que el límite no existe.
3 Ahora se nos pide calcular
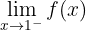
el cual se refiere al límite por la izquierda. Observemos que, cuando  se aproxima a
se aproxima a  por la izquierda, la función decrece infinitamente. Por tanto, el límite es
por la izquierda, la función decrece infinitamente. Por tanto, el límite es
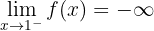
4 El cuarto límite es

que se trata ahora del límite por la derecha. Por lo tanto,
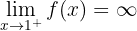
5 Por último se nos pide el límite

el cual es muy similar al primer límite. Podemos observar que  crece indefinidamente,
crece indefinidamente,  también crece indefinidamente. Por lo tanto,
también crece indefinidamente. Por lo tanto,
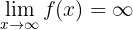
Calcula el límite

Deseamos encontrar el límite
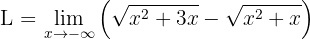
Notemos, primero, que si "evaluamos en infinito", obtenemos una forma indeterminada:
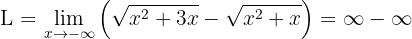
Como el valor de  no está determinado, necesitamos realizar una manipulación algebraica de nuestra función.
no está determinado, necesitamos realizar una manipulación algebraica de nuestra función.
Antes de hacer la manipulación algebraica, transformemos el límite utilizando la propiedad:
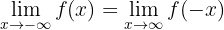
Con lo que el límite resulta ser:
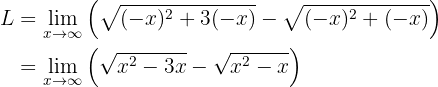
Ahora necesitamos manipular algebraicamente los límites con el fin de eliminar la resta de infinitos. Esto se logra "racionalizando" (es decir, multiplicar y dividir por el conjugado):
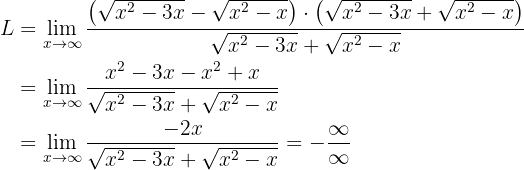
Observemos que si evaluamos en infinito, volvemos a tener una nueva indeterminación. En este caso se trata de una indeterminación 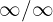 . Para deshacernos de esta indeterminación debemos realizar otra manipulación algebraica. En este caso se trata de multiplicar y dividir por
. Para deshacernos de esta indeterminación debemos realizar otra manipulación algebraica. En este caso se trata de multiplicar y dividir por 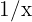 :
:
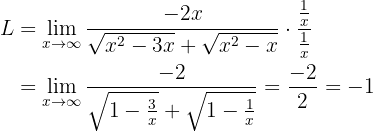
El cual es el resultado que buscábamos.
Calcula el límite
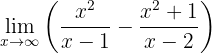
Ahora tenemos el límite:

Notemos que si evaluamos en infinito directamente, obtenemos:
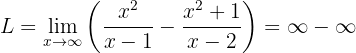
Para deshacernos de esta indeterminación podemos sumar las fracciones (utilizando el común denominador)
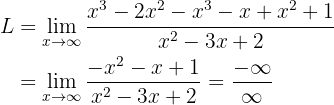
Como ahora tenemos una indeterminación de la forma 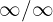 , entonces buscaremos multiplicar y dividir por un término apropiado para evitar la indeterminación. El término apropiado es el monomio de mayor grado en el numerador o denominador, es decir,
, entonces buscaremos multiplicar y dividir por un término apropiado para evitar la indeterminación. El término apropiado es el monomio de mayor grado en el numerador o denominador, es decir, 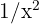 . Por lo tanto, nos queda:
. Por lo tanto, nos queda:
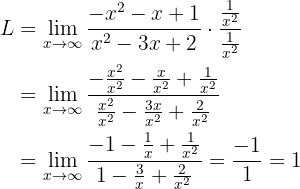
Por lo que el límite es  .
.
Calcula el límite

Si evaluamos en infinito, obtenemos lo siguiente:
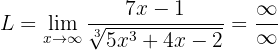
La cual es una indeterminación de 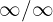 . Por lo tanto, debemos multiplicar y dividir entre el monomio de mayor grado (ya sea en numerador o denominador). En este caso es
. Por lo tanto, debemos multiplicar y dividir entre el monomio de mayor grado (ya sea en numerador o denominador). En este caso es 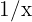 —como el denominador involucra una raíz cúbica, entonces el "monomio"
—como el denominador involucra una raíz cúbica, entonces el "monomio"  se considera como un monomio de grado 1—. Así:
se considera como un monomio de grado 1—. Así:
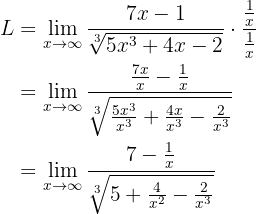
Que al "evaluar en infinito" tenemos:

Evalúa el límite
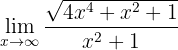
Si evaluamos la función en infinito, obtenemos:

Por tanto, al ser una forma indeterminada, debemos multiplicar y dividir por el monomio de mayor grado ( ; recordemos que las potencias del numerador las dividimos por 2 ya que se encuentran dentro de una raíz cuadrada):
; recordemos que las potencias del numerador las dividimos por 2 ya que se encuentran dentro de una raíz cuadrada):
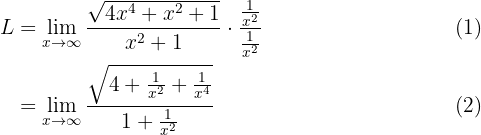
Luego, evaluando en infinito, tenemos:
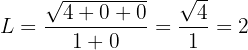
Por tanto, el límite es 2.
Evalúa el límite
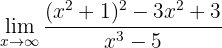
Si evaluamos la función en infinito, de inmediato podemos ver que:
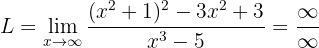
Por lo tanto, debemos realizar una manipulación algebraica para poder deshacernos de la indeterminación.
Este límite lo podemos resolver de dos maneras.
1 Por comparación de infinitos:
Primero expandemos el binomio al cuadrado, así obtenemos

Notemos que en el numerador obtenemos  mientras que en el denominador tenemos
mientras que en el denominador tenemos  como los términos de mayor grado. Por consiguiente, el grado del numerador es mayor y el límite será
como los términos de mayor grado. Por consiguiente, el grado del numerador es mayor y el límite será  . Recordemos que cuando grado del numerador es mayor, entonces el límite es
. Recordemos que cuando grado del numerador es mayor, entonces el límite es  si los términos de mayor grado tienen el mismo signo.
si los términos de mayor grado tienen el mismo signo.
2 Dividiendo numerador y denominador por el término de mayor grado:
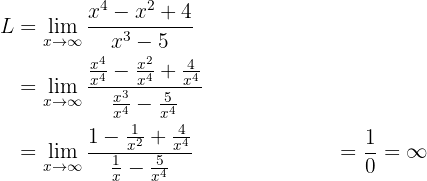
Observemos que, en general,  es una forma indeterminada. Sin embargo, estamos calculando un límite cuando
es una forma indeterminada. Sin embargo, estamos calculando un límite cuando  , además, tanto el numerador como el denominador son positivos conforme
, además, tanto el numerador como el denominador son positivos conforme  crece, Por lo tanto, podemos concluir que el límite será
crece, Por lo tanto, podemos concluir que el límite será  .
.
Calcula el límite

Si evaluamos en infinito, tenemos:

Sin embargo, el infinito del denominador tiene un orden superior. Por lo tanto, podemos concluir que 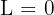 .
.
No obstante, demostrar que el límite es 0 sin utilizar L'Hopital o criterio del "orden" es complicado. Para hacerlo, denotemos:
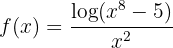
Para encontrar el límite, debemos buscar dos funciones  y
y  tales que
tales que  y
y

Si encontramos estas funciones, entonces podemos concluir que 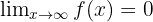 .
.
En primer lugar, observemos que cuando 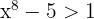 , entonces
, entonces 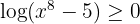 (y esto se cumple cuando
(y esto se cumple cuando  es grande). Asimismo, tenemos que
es grande). Asimismo, tenemos que  para
para 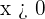 . Por lo tanto, tenemos que:
. Por lo tanto, tenemos que:
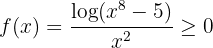
cuando  "es suficientemente grande". Así, tenemos que
"es suficientemente grande". Así, tenemos que 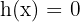 donde es claro que
donde es claro que 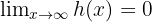 .
.
Para encontrar la segunda función, primero notemos que 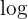 es una función creciente, por lo tanto, debido a que
es una función creciente, por lo tanto, debido a que  , entonces
, entonces  . Así, tenemos que
. Así, tenemos que
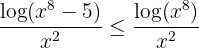
ahora, si tomamos  , entonces podemos escribir
, entonces podemos escribir
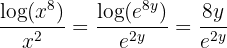
Una propiedad muy importante sobre la función exponencial es
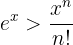
para cualquier  y
y 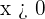 . Si tomamos
. Si tomamos 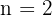 , entonces tenemos
, entonces tenemos

De aquí se sigue que
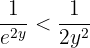
Por lo tanto, tenemos que
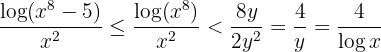
Así, 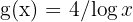 donde
donde  . Además,
. Además, 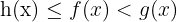 . Por lo tanto,
. Por lo tanto, 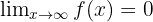 .
.
Calcula el límite
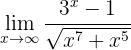
Si evaluamos en  , entonces obtenemos
, entonces obtenemos
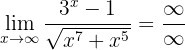
También aquí podemos observar el "órden" del denominador y numerador para determinar el límite. En este caso el numerador tiene un límite de orden superior, por lo tanto,
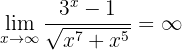
Para demostrarlo, denotemos

y debemos encontrar una función  tal que
tal que  y
y 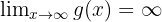 . En primer lugar, observemos que cuando
. En primer lugar, observemos que cuando  , entonces
, entonces  (es decir, el radicando es positivo para un
(es decir, el radicando es positivo para un  lo suficientemente grande). Además,
lo suficientemente grande). Además,  cuando
cuando  , por lo tanto
, por lo tanto
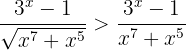
Ahora notemos que si  , entonces
, entonces 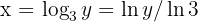 . De aquí se sigue que
. De aquí se sigue que

Por tanto, 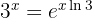 . Asimismo, como sabemos que
. Asimismo, como sabemos que
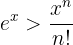
cuando 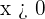 , entonces tenemos que
, entonces tenemos que
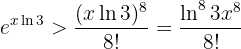
Así, tenemos que
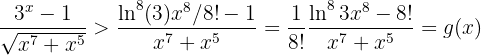
donde 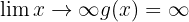 . Por lo tanto, el límite es
. Por lo tanto, el límite es
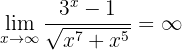
Calcula el límite
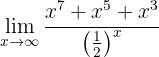
Al evaluar en infinito, tenemos que

Por lo tanto, el límite debe ser infinito, pues tanto el numerador como el denominador son positivos para un  suficientemente grande. Para verlo de forma más clara, notemos que
suficientemente grande. Para verlo de forma más clara, notemos que
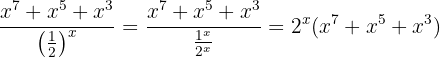
Por tanto,
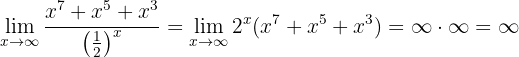
Calcula el límite
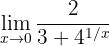
Si evaluamos en 0, tenemos

donde tenemos una forma indeterminada de la forma  . Notemos que en este caso no podemos decir que
. Notemos que en este caso no podemos decir que  ya que estamos calculando un límite cuando
ya que estamos calculando un límite cuando 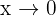 y
y  es positivo o negativo cerca del 0 (cuando calculamos límites
es positivo o negativo cerca del 0 (cuando calculamos límites  esto no suele ser un problema).
esto no suele ser un problema).
Por tanto, debemos calcular los límites laterales:
1 Primero calculamos el límite por la izquierda
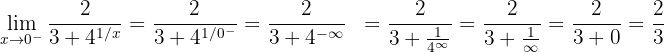
2 Ahora calculamos el límite por la derecha
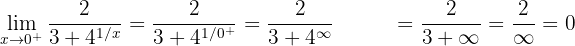
Aquí podemos observar que los dos límites laterales son diferentes, por lo tanto, el límite cuando 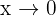 no existe.
no existe.
Calcula el límite
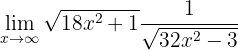
Si "evaluamos en infinito", obtenemos

Por lo tanto, debemos realizar una manipulación algebraica. Primero escribamos el límite como una sola fracción:
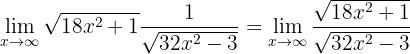
Ahora dividamos el numerador y denominador por el coeficiente de mayor grado (es decir  ya que se encuentra dentro de una raíz):
ya que se encuentra dentro de una raíz):
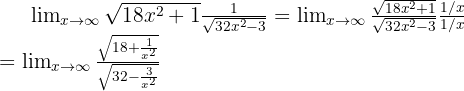
Ahora ya podemos evaluar en infinito, de modo que obtenemos:
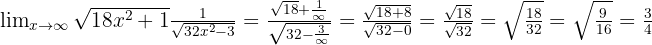
Por lo tanto, el límite es 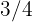 .
.
Encuentra el límite
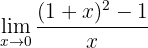
Si evaluamos en 0, podemos observar que
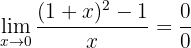
por lo que tenemos una indeterminación y necesitamos realizar una manipulación algebraica. Para esto, expandemos el binomio al cuadrado:
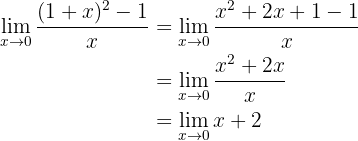
Si evaluamos ahora en 0, obtenemos:
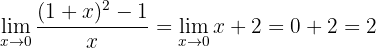
Por tanto, el límite es 2.
Evalúa el límite

Si evaluamos en 3, obtendremos
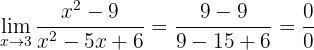
Por lo que podemos observar que tenemos, de nuevo, una forma indeterminada. Para evitar la indeterminación factorizaremos tanto el numerador como el denominador (observemos que el numerador es una diferencia de cuadrados; mientras que el denominador se puede factorizar al encontrar un par de números que multiplicados resulten 6 y que sumados resulten -5):
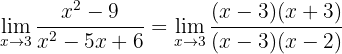
De este modo, podemos cancelar  para tener
para tener

Así, el límite es 6.
Calcula el límite
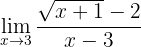
Si evaluamos la función en 3, observamos que
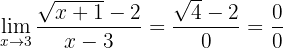
De modo que tenemos una indeterminación y debemos realizar una manipulación algebraica. En este caso, como tenemos una expresión con radicales, debemos multiplicar y dividir la fracción por el conjugado del numerador (ya que es el que tiene el radical):
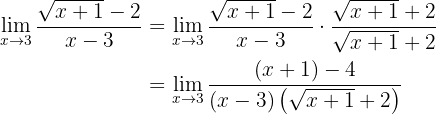
lo cual se obtiene debido a que tenemos unos "binomios conjugados" en el numerador. Simplificando:
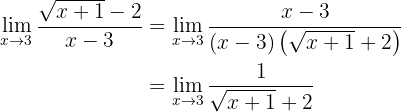
Ahora sí podemos evaluar en 3, de donde obtenemos:
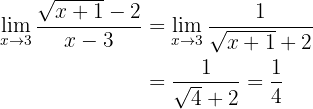
Por tanto, el límite es 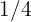 .
.
Calcula el límite

Si evaluamos en  , obtendremos:
, obtendremos:

La cual es una forma indeterminada. Por lo tanto, debemos realizar manipulaciones algebraicas para obtener alguna expresión similar a la definición de  . Para ello, primero sumamos y restamos 2 en el exponente (denotaremos al límite como
. Para ello, primero sumamos y restamos 2 en el exponente (denotaremos al límite como  ):
):
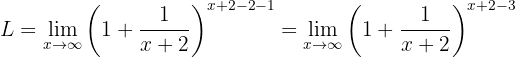
Luego utilizamos propiedades de los exponentes:

Observemos que la primera potencia coincide con la definición de  con
con  . Por lo tanto, el límite es:
. Por lo tanto, el límite es:
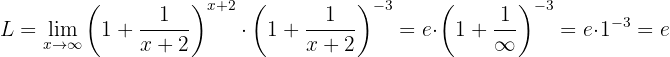
Calcula el límite
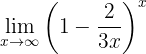
Al evaluar en infinito, tenemos:

Por tanto, debemos realizar una manipulación algebraica para obtener una expresión similar a la definición de  . Para hacerlo, primero modificamos la expresión que tenemos dentro de los paréntesis (y denotamos como
. Para hacerlo, primero modificamos la expresión que tenemos dentro de los paréntesis (y denotamos como  al límite):
al límite):

Por tanto, en el exponente debemos tener  de alguna manera. Observemos que esto se logra al hacer:
de alguna manera. Observemos que esto se logra al hacer:

Luego utilizamos propiedades de los exponentes:
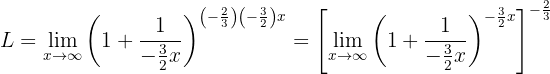
Ahora podemos calcular el límite (notando que lo que está dentro de los corchetes cuadrados es la definición de  con
con 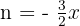 ):
):
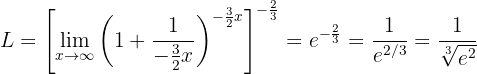
Calcula el límite
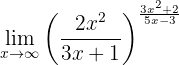
Si evaluamos en  , de inmediato vemos que tenemos:
, de inmediato vemos que tenemos:
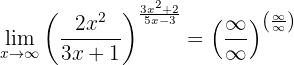
Para resolverlo, utilizaremos comparación de infinitos en las dos fracciones. Primero notemos que
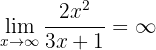
ya que el numerado es un polinomio de mayor grado (y los coeficientes principales tienen el mismo signo). Similarmente,
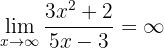
por el mismo motivo. Por lo tanto, el límite es:

ya que la última expresión no se trata de una forma indeterminada.
Determina el límite
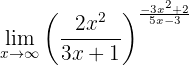
De nuevo, si evaluamos en infinito obtendremos:
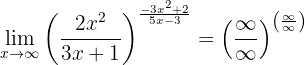
No obstante, si resolvemos los límites de las fracciones (comparando los órdenes de los infinitos), podemos observar que:

ya que el numerador es un polinomio de mayor grado y los coeficientes principales tienen el mismo signo. Por otro lado,
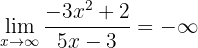
porque el numerador es un polinomio de mayor grado, pero los coeficientes principales tienen signo diferente. De este modo, tenemos que el límite es:

Determina el siguiente límite:
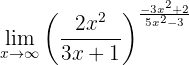
De nuevo, si evaluamos al infinito tenemos que

Por tanto, evaluamos los límites de las fracciones por separado. En la base de la potencia tenemos que el numerador es un polinomio de mayor grado, además de que los coeficientes principales tienen el mismo signo, por lo tanto

Por otro lado, en el exponente tanto el numerador como el denominador son polinomios con el mismo orden. Por consiguiente, el límite es el cociente de los coeficientes principales:
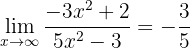
Por lo tanto, el límite es

ya que  si
si  .
.
Evalúa el siguiente límite:
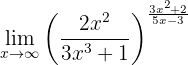
Si evaluamos al infinito tenemos que
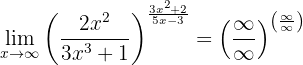
Por lo que tenemos que evaluar los límites de las fracciones por separado para determinar el límite general. Tenemos que
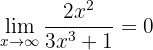
ya que el denominador es un polinomio de mayor grado. Asimismo,
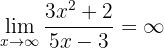
debido a que el numerador es un polinomio de mayor grado y los coeficientes principales tienen el mismo signo. Por lo tanto, el límite es

debido a que 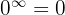 (es decir, no es una forma indeterminada).
(es decir, no es una forma indeterminada).
Evalúa el siguiente límite:
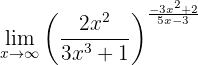
Este límite es prácticamente igual al anterior, con solo un signo de diferencia.

Así que tenemos que evaluar los límites de las fracciones por separado para determinar el límite general. Al igual que en el caso anterior, tenemos que
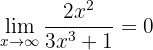
ya que el denominador es un polinomio de mayor grado. Asimismo, tenemos que
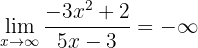
debido a que el numerador es un polinomio de mayor grado y los coeficientes principales tienen signo distinto. Por lo tanto, el límite es

notemos que esta sí es una forma indeterminada. Por lo tanto, debemos utilizar la propiedad:

de manera que
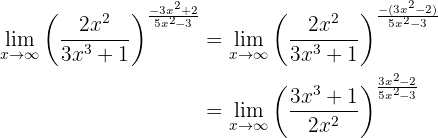
En este caso,

Por lo que
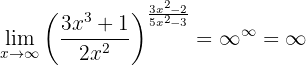
Nota: es importante escribirlo de esta manera. El motivo es que  sí es una forma indeterminada (es decir, podemos construrir distintas funciones donde esa forma indeterminada "converja" a un valor distinto).
sí es una forma indeterminada (es decir, podemos construrir distintas funciones donde esa forma indeterminada "converja" a un valor distinto).
Evalúa el siguiente límite:

Al igual que en los casos anteriores, si evaluamos en infinito, obtenemos

Y al igual que en los casos anteriores, calculamos los límites de cada fracción por separado:
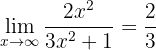
ya que el numerador y el denominador son polinomios del mismo grado (por lo que el límite es el cociende de los coeficientes principales). Asimismo, tenemos que

de forma que el límite es

Evalúa el siguiente límite:

Como en los casos anteriores, al evaluar en infinito tenemos
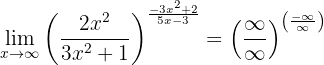
Calculamos los límites de cada fracción por separado:
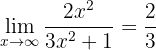
ya que el numerador y el denominador son polinomios del mismo grado (por lo que el límite es el cociende de los coeficientes principales). Además, tenemos que
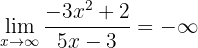
puesto que el numerador es un polinomio de mayor grado y los coeficientes principales tienen signos diferentes. Así, el límite es

ya que tenemos un una expresión de la forma 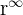 donde
donde  .
.
Determina el siguiente límite:
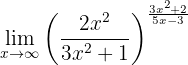
Como en los casos anteriores, al evaluar en infinito tenemos
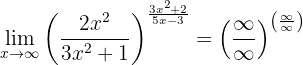
nota que la función es prácticamente la misma que la anterior, pero con solo un signo cambiado. Calculamos los límites de cada fracción por separado:
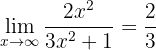
ya que el numerador y el denominador son polinomios del mismo grado (por lo que el límite es el cociende de los coeficientes principales). Además, tenemos que
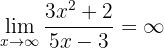
debido a que el numerador es un polinomio de mayor grado y los signos de los coeficientes principales son iguales. De esta forma, el límite es
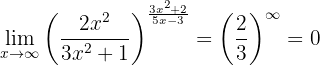
ya que tenemos un una expresión de la forma 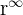 donde
donde 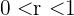 .
.
Si buscas un profe de mates, ya prefieras un profesor de matematicas online o uno que se desplace a domicilio, encontrarás el que mejor se adapte a ti en Superprof.
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.
Podrían mostrar los pares ordenados para graficarlo, gracias