Capítulos
Definición de valor absoluto
El valor absoluto es una función, denotada como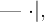 
que se encuentra definida sobre todos los números reales y que devuelve, por cada número real, su respectivo valor positivo.
Por ejemplo, para un número real positivo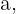 
su valor absoluto 
será igual a él mismo, o sea 
Mientras que para un número real negativo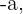 
tendrá como valor absoluto a 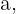por lo tanto 
Funciones a trozos
Una función a trozos es una función que tiene definiciones distintas en "trozos" (o conjuntos de números) distintos. Por ejemplo
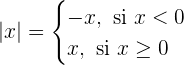
es una función a trozos.
Como podemos ver, hemos definido de manera sencilla la función valor absoluto representándola como una función a trozos. Ésta es una técnica común al estudiar funciones en valor absoluto, pues al expresarlas como funciones a trozos será más fácil graficarlas y entender su comportamiento.
Transformación a función a trozos
Las funciones en valor absoluto se transforman en funciones a trozos, siguiendo los siguientes pasos:
- Se iguala a cero la función, sin el valor absoluto, y se calculan sus raíces.
- Se forman intervalos con las raíces y se evalúa el signo de cada intervalo.
- Definimos la función a trozos, teniendo en cuenta que en los intervalos donde la
es negativa se cambia el signo de la función. - Representamos la función resultante.
Ejemplos
Resolveremos los siguientes problemas usando los pasos anteriores
1.Transformar la función valor absoluto 
en una función a trozos.
Paso 1. Debemos igualar a cero la función, sin el valor absoluto, y calcular las raíces de la ecuación resultante.
Igualando a cero
y sumando 3 en ambos lados de la igualdad anterior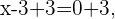 
tenemos que 
. En este caso, 3 es raíz de la ecuación.
Paso 2. Se forman intervalos con la raíz y se evalúa el signo de cada intervalo.
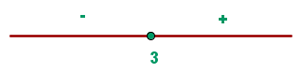
Dado que el valor de la raíz es 
este es nuestro punto de referencia. Tal y como vemos en la figura la ecuación será positiva si tomamos valores de mayores a 
y negativa si tomamos valores de menores a .
Paso 3. Definimos la función a trozos, teniendo en cuenta que en los intervalos donde es negativo se cambia el signo de la función.
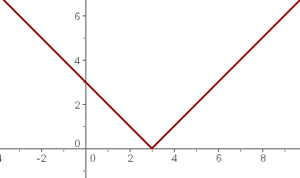
Paso 4. Finalmente podemos representar la función graficamente. Ya que es la raíz de nuestra ecuación inicial, entonces es nuestro punto de referencia, entonces la función será decreciente para valores menores a y creciente para valores mayores a tal y como se oberva en la figura.
2.Transformar la función valor absoluto 
en una función a trozos.
Paso 1. Igualamos a cero la función, sin el valor absoluto, y se calculan sus raíces.
En este caso, nuestra ecuación es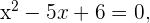 
y utilizando la fórmula para resolver ecuaciones de segundo grado
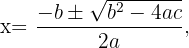
donde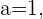 
y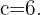 
Entonces, tenemos que
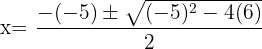
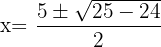
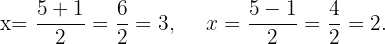
Paso 2. Se forman intervalos con la raíces y se evalúa el signo de cada intervalo.
Al evaluar la ecuación en distintos valores, por ejemplo para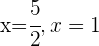 
y
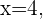tenemos que
Esto quiere decir que la ecuación toma valores negativos para 
y valores positivos para 
y 
tal y como vemos en la figura.
Paso 3. Dada la información anterior podemos definir la función a trozos, teniendo en cuenta que en los intervalos donde la x es negativa se cambia el signo de la función
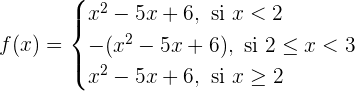
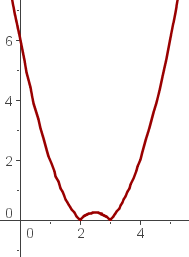
Paso 4. Finalmente representamos la función graficamente.
Ya que la función es cuadratica, la grafica debe ser similar a una parábola, solo debemos tener en cuenta los lugares donde la función es positiva, negativa y donde se anula.
Podemos ver cómo la grafica coincide con la información obtenida anteriormente
¿Te ha gustado este artículo? ¡Califícalo!
Cargando...
Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
El Punto de inflexión en el ejercicio 2: f(x) = x^3 + x + 1 debe ser (0, 1)
Hola agradecemos tu comentario, tenias razón era un error que ya se corrigió.
la grafica esta mal echa de signos de cada cuadrante
Hola te agradecemos por visitar nuestra pagina, podrías mencionar el número de ejercicio para poder rectificar esos errores que mencionas.
Se podría añadir un poco más de explicación a por que se hace cada paso ( ejemplo porque se divide todo por x ^2?)
Hola agradecemos que puedas darnos tu opinión, cuando surja una duda en este espacio de los comentarios estaremos atentos para darte una explicación con respecto a algo que no entiendas, exista un error o se pueda mejorar una explicación, solo comunícalo y te contestaremos.