Escoge la función a la que corresponde cada una de las siguientes gráficas:
Selecciona una respuesta.
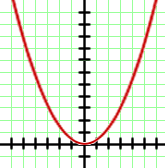
La gráfica dada es una dilatación de la parábola  , puesto que es más "achatada" que esta.
, puesto que es más "achatada" que esta.
Por tanto, podemos deducir que es la tercera opción, es decir, 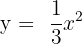 También podemos reconocer la opción correcta sin más que dar algunos valores. Por ejemplo, la gráfica muestra que la función debe pasar por el punto
También podemos reconocer la opción correcta sin más que dar algunos valores. Por ejemplo, la gráfica muestra que la función debe pasar por el punto  , y podemos comprobar que la única opción que verifica esto es la tercera.
, y podemos comprobar que la única opción que verifica esto es la tercera.
Selecciona una respuesta.
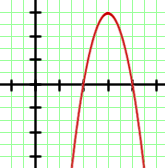
Se trata de una parábola con las ramas hacia abajo por lo que el coeficiente que acompaña al término de segundo grado debe ser negativo. Así, podemos descartar la primera opción. Para saber cuál de las dos opciones restantes es la correcta basta comprobar alguno de los puntos de la gráfica.
Por ejemplo, el punto  debe ser un punto de la misma.
debe ser un punto de la misma.
Si tomamos  en la segunda opción obtenemos
en la segunda opción obtenemos 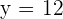 , con lo que también podemos descartar esta función.
, con lo que también podemos descartar esta función.
Por tanto, la solución del ejercicio es la tercera expresión dada, es decir, 

Selecciona una respuesta.
La gráfica dada es una traslación de la parábola 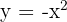 .
.
Al estar trasladada una unidad hacia arriba nos indica que el término independiente debe ser 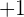 , con lo que la opción correcta es la primera, es decir,
, con lo que la opción correcta es la primera, es decir,  .
.
También podemos resolver el ejercicio tomando algún (o algunos) punto de la gráfica y comprobando para qué expresión se cumple.
Por ejemplo, la gráfica dada pasa por el punto 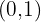 y, tomando
y, tomando  , sólo obtenemos
, sólo obtenemos 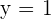 con la primera función, lo que nos lleva a que esta es la correcta.
con la primera función, lo que nos lleva a que esta es la correcta.
Selecciona una respuesta.
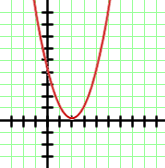
La gráfica es una parábola con las ramas hacia arriba, por lo que el coeficiente del término de segundo grado debe ser positivo. Entonces, la última expresión queda descartada.
Observando la gráfica tenemos que para  y debe valer
y debe valer  , lo cual sólo se verifica para la segunda opción (
, lo cual sólo se verifica para la segunda opción (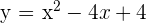 ), lo que nos lleva a que esta es la correcta.
), lo que nos lleva a que esta es la correcta.
Escoge la gráfica a la que corresponde cada una de las siguientes funciones:
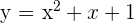
a 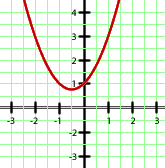
b 
c 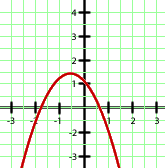
Selecciona una respuesta.
Por ser positivo el coeficiente que acompaña al término de segundo grado se trata de una parábola con las ramas hacia arriba, con lo que la tercera opción queda descartada. Por otro lado, para  se tiene
se tiene 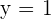 y podemos observar que
y podemos observar que 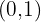 es punto de la primera gráfica pero no de la segunda. Por tanto, la opción correcta es la primera.
es punto de la primera gráfica pero no de la segunda. Por tanto, la opción correcta es la primera.
Como hemos comprobado es fácil resolver el ejercicio sin más que fijarnos en ciertos detalles relevantes. De todas formas, si queremos dibujar una parábola a partir de su expresión analítica conviene seguir un procedimiente general, como sigue:
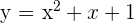
En primer lugar, observemos que el coeficiente del término de segundo grado es positivo ( ), con lo que la parábola tendrá las ramas hacia arriba, es decir, la gráfica será de la forma:
), con lo que la parábola tendrá las ramas hacia arriba, es decir, la gráfica será de la forma:

Vértice

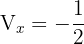
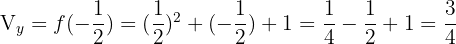
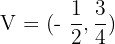
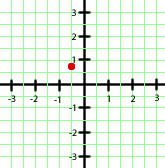
Con los datos que tenemos podemos hacernos una idea de cómo será la gráfica de nuestra parábola:
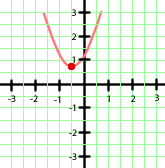
Cortes con los ejes.
Corte con el eje 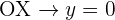
Mirando el esbozo que ya hemos hecho podemos deducir que esta parábola no tiene cortes con el eje de coordenadas. Pero también podemos hacerlos resolviendo la ecuación de segundo grado como se muestra a continuación:
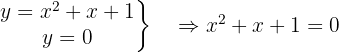
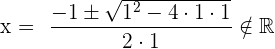
Por tanto, no hay ningún corte con el eje  .
.
Corte con el eje 
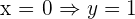
Corte 
Ya sabemos otro punto por donde pasará la gráfica:
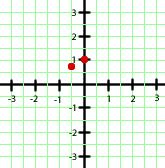
Tabla de valores.
 |  |
|---|---|
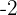 |  |
 |  |
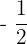 |  |
 |  |
 |  |
Ya tenemos puntos suficientes con los que dibujar la gráfica de la parábola:

Por tanto, la gráfica de la parábola 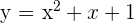 es:
es:
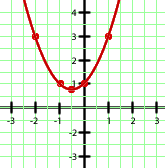

a
b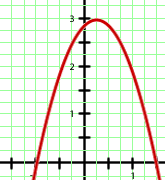
c
Selecciona una respuesta.
Por ser positivo el coeficiente que acompaña al término de segundo grado se trata de una parábola con las ramas hacia arriba, con lo que la segunda opción queda descartada. Por otro lado, para  se tiene
se tiene 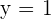 y podemos observar que
y podemos observar que 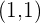 es punto de la primera gráfica pero no de la tercera. Por tanto, la opción correcta es la primera.
es punto de la primera gráfica pero no de la tercera. Por tanto, la opción correcta es la primera.
Procedimiento general:

En primer lugar, observemos que el coeficiente del término de segundo grado es positivo 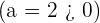 , con lo que la parábola tendrá las ramas hacia arriba, es decir, la gráfica será de la forma:
, con lo que la parábola tendrá las ramas hacia arriba, es decir, la gráfica será de la forma:

Vértice

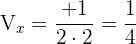
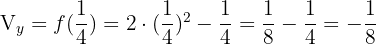
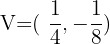
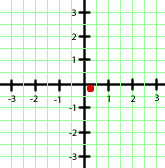
Con los datos que tenemos podemos hacernos una idea de cómo será la gráfica de nuestra parábola:

Cortes con los ejes.
Corte con el eje 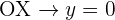
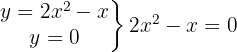
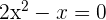

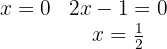 Corte
Corte 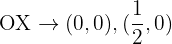
Corte con el eje 
 Corte
Corte 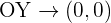
Ya sabemos otros puntos de la gráfica:

Tabla de valores.
 |  |
|---|---|
 |  |
 |  |
 | 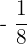 |
 |  |
 |  |
Ya tenemos puntos suficientes con los que dibujar la gráfica de la parábola:
Por tanto, la gráfica de la parábola  es:
es:

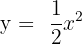
a 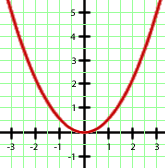
b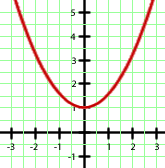
c
Selecciona una respuesta.
Se trata de una dilatación de la parábola  . Así, la segunda opción queda descartada, puesto que aunque sea una dilatación también es una traslación. Además, al ser una dilatación (el coeficiente de
. Así, la segunda opción queda descartada, puesto que aunque sea una dilatación también es una traslación. Además, al ser una dilatación (el coeficiente de 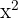 es un número entre 0 y 1) debe ser más "ancha" que la parábola
es un número entre 0 y 1) debe ser más "ancha" que la parábola  . Por tanto, la opción correcta es la primera.
. Por tanto, la opción correcta es la primera.
Procedimiento general:
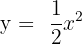 En primer lugar, observemos que el coeficiente del término de segundo grado es positivo
En primer lugar, observemos que el coeficiente del término de segundo grado es positivo 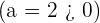 , con lo que la parábola tendrá las ramas hacia arriba, es decir, la gráfica será de la forma:
, con lo que la parábola tendrá las ramas hacia arriba, es decir, la gráfica será de la forma:

Vértice

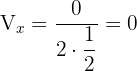
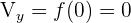
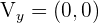
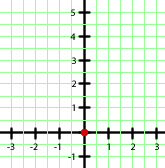
Con los datos que tenemos podemos hacernos una idea de cómo será la gráfica de nuestra parábola:

Cortes con los ejes.
Corte con el eje 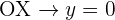
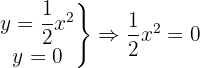
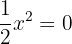

Corte 
Corte con el eje 
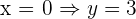 Corte
Corte 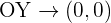
Tabla de valores.
 |  |
|---|---|
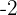 |  |
 |  |
 |  |
 |  |
 |  |
Ya tenemos puntos suficientes con los que dibujar la gráfica de la parábola:
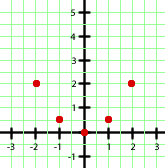
Por tanto, la gráfica de la parábola 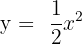 es:
es:
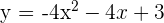
a
b
c
Selecciona una respuesta.
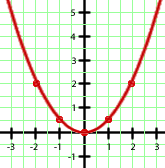
Por ser negativo el coeficiente que acompaña al término de segundo grado se trata de una parábola con las ramas hacia abajo, con lo que la priemra opción queda descartada. Por otro lado, para 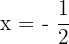 se tiene
se tiene 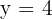 y podemos observar que
y podemos observar que 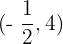 es punto de la segunda gráfica pero no de la tercera. Por tanto, la opción correcta es la segunda.
es punto de la segunda gráfica pero no de la tercera. Por tanto, la opción correcta es la segunda.
Procedimiento general:
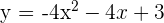
En primer lugar, observemos que el coeficiente del término de segundo grado es negativo 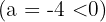 , con lo que la parábola tendrá las ramas hacia abajo, es decir, la gráfica será de la forma:
, con lo que la parábola tendrá las ramas hacia abajo, es decir, la gráfica será de la forma:

Vértice

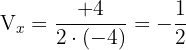
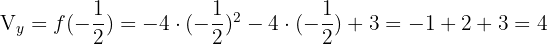
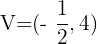

Con los datos que tenemos podemos hacernos una idea de cómo será la gráfica de nuestra parábola:
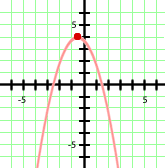
Cortes con los ejes.
Corte con el eje 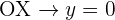
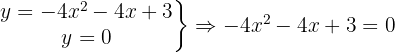
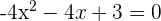

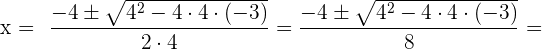
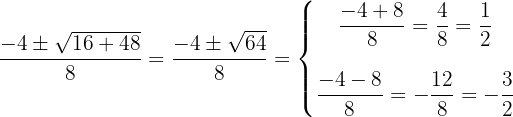 Corte
Corte 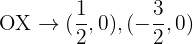
Corte con el eje 
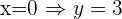 Corte
Corte

Tabla de valores.
 |  |
|---|---|
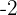 |  |
 |  |
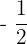 |  |
 |  |
 |  |
Ya tenemos puntos suficientes con los que dibujar la gráfica de la parábola:
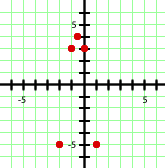
Por tanto, la gráfica de la parábola 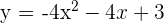 es:
es:

Si tienes dudas puedes consultar la teoría o buscar alguna clase de algebra basica en nuestra plataforma.
Resumir con IA:



Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Felicitaciones, muy interesantes los problemas y sobretodo las gráficas. ¿Pueden indicarme que programa utilizan?
Hola te agradecemos tu comentario, si te refieres a graficar te recomendamos geogebra, symbolat y otros mas.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.