Capítulos

Crecimiento y decrecimiento en un punto
Función estrictamente creciente

 es estrictamente creciente en
es estrictamente creciente en  si sólo si existe un entorno
si sólo si existe un entorno 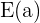 de
de  , tal que para toda
, tal que para toda  que pertenezca al entorno de
que pertenezca al entorno de  se cumple:
se cumple:
1 Si 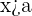 entonces
entonces 
2 Si 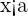 entonces
entonces 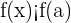
La tasa de variación es positiva, ya que si  es estrictamente creciente en
es estrictamente creciente en  , entonces
, entonces 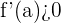 .
.
Función creciente

 es creciente en
es creciente en  si sólo si existe un entorno
si sólo si existe un entorno 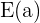 de
de  , tal que para toda
, tal que para toda  que pertenezca al entorno de
que pertenezca al entorno de  se cumple:
se cumple:
1 Si 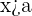 entonces
entonces 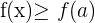
2 Si 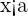 entonces
entonces 
La tasa de variación es positiva o igual a cero, ya que si  es creciente en
es creciente en  , entonces
, entonces 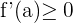 .
.
Función estrictamente decreciente
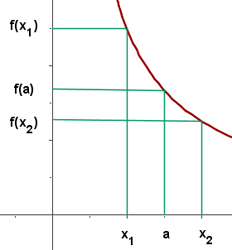
 es estrictamente decreciente en
es estrictamente decreciente en  si sólo si existe un entorno
si sólo si existe un entorno 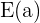 de
de  , tal que para toda
, tal que para toda  que pertenezca al entorno de
que pertenezca al entorno de  se cumple:
se cumple:
1 Si 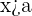 entonces
entonces 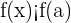
2 Si 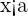 entonces
entonces 
La tasa de variación es negativa, ya que si  es estrictamente decreciente en
es estrictamente decreciente en  , entonces
, entonces  .
.
Función decreciente
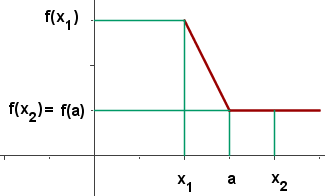
 es decreciente en
es decreciente en  si sólo si existe un entorno
si sólo si existe un entorno 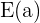 de
de  , tal que para toda
, tal que para toda  que pertenezca al entorno de
que pertenezca al entorno de  se cumple:
se cumple:
1 Si 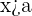 entonces
entonces 
2 Si 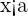 entonces
entonces 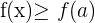
La tasa de variación es negativa o igual a cero, ya que si  es decreciente en
es decreciente en  , entonces
, entonces  .
.
Intervalos de crecimiento y decrecimiento
Para hallar el crecimiento y decrecimiento seguiremos los siguientes pasos:
1 Derivar la función  .
.
2 Obtener las raíces de la derivada primera, para ello hacemos: 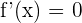 .
.
3 Formamos intervalos abiertos con los ceros (raíces) de la derivada primera y los puntos de discontinuidad de la función original (si los hubiese).
4 Tomamos un valor de cada intervalo, y hallamos el signo que tiene en la derivada primera.
Si 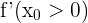 , entonces
, entonces  es creciente en todos los puntos del intervalo al que pertenece
es creciente en todos los puntos del intervalo al que pertenece 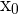 .
.
Si 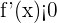 , entonces
, entonces  es decreciente en todos los puntos del intervalo al que pertenece
es decreciente en todos los puntos del intervalo al que pertenece 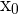 .
.
5 Escribimos los intervalos de crecimiento y decrecimiento.
Ejemplo de cálculo de intervalos de crecimiento y decrecimiento
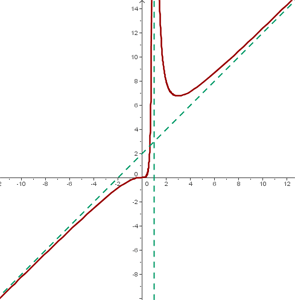
Calcular los intervalos de crecimiento y decrecimiento de la función:
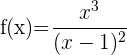
En primer lugar calculamos el dominio para saber donde está definida la función
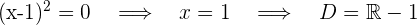
Derivamos la función

Igualamos la derivada a cero y obtenemos las raíces de la ecuación

Formamos intervalos con los ceros de la derivada primera y con los puntos de discontinuidad
Sustituimos un valor de cada intervalo en la función
Si el resultado es positivo, la función es creciente en ese intervalo
Si el resultado es negativo, la función es decreciente en ese intervalo

La función es creciente en los intervalos 
La función es decreciente en los intervalos 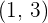
Resumir con IA:













Apuntes es una plataforma dirigida al estudio y la práctica de las matemáticas a través de la teoría y ejercicios interactivos que ponemos a vuestra disposición. Esta información está disponible para todo aquel/aquella que quiera profundizar en el aprendizaje de esta ciencia. Será un placer ayudaros en caso de que tengáis dudas frente algún problema, sin embargo, no realizamos un ejercicio que nos presentéis de 0 sin que hayáis si quiera intentado resolverlo. Ánimo, todo esfuerzo tiene su recompensa.
Cual es un buen graficador de funciones con cuadricula en el fondo y ejes coordenados para graficar funciones.He visto uno elaborado por Mariluna Saldivar Pat titulado «¿Que es una funcion lineal? pero no se con que programa hizo el dibujo
Hola en internet esta geogebra y simbolab que son los que yo uso, creo que si preguntas en el buscador te recomiendan otros muy buenos, los que mencione antes trabajo muy bien con ellos y los recomiendo.
Me ayudarian hacer la funcion lineal con grafico
Y=2×+1
La primera derivada se anula en x = 3. Por lo tanto 3 es otro punto crítico de la función del ejemplo.
Hola gracias por la observación, podrías hacernos el favor de mostrarnos la función que se deriva y se encuentran los puntos críticos.
Hola con gusto lo haremos, pero podrías señalar en que ejercicio quieres que lo hagamos, para poder ayudarte.
Podrían mostrar los pares ordenados para graficarlo, gracias